In fluid Mechanics, There are different types of Fluid flow, and a Study of these types of fluid flows will help us determine the flow discharge, velocity and acceleration of the fluids. Once the velocity is known, then the pressure distribution and forces acting on the fluid can be determined effortlessly. Let us discuss these types of Fluid flows in detail.

Types of Fluid Flows
Following are the different types of fluid flows which help us determine the velocity and the acceleration of the fluid.
- Steady and unsteady flows
- Uniform and non-uniform flows
- Laminar and turbulent flows
- Compressible and incompressible flows
- Rotational and irrotational flows
- One, two and three-dimensional flows
1. Steady and unsteady flows
Steady flow is defined as that type of flow in which the fluid characteristics like velocity, pressure, density, etc., at a point do not change with time.
Thus for a steady flow, mathematically, we can write
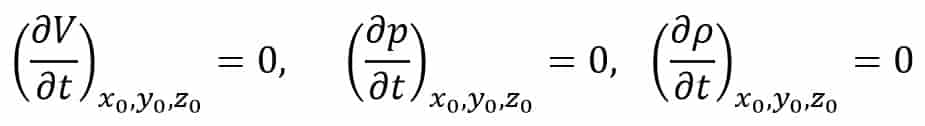
Where (x0, y0, z0) is a fixed point in a fluid field.
Unsteady flow is that type of flow, in which the velocity, pressure or density at a point changes with respect to time.
Thus, mathematically, for unsteady flow, we can write
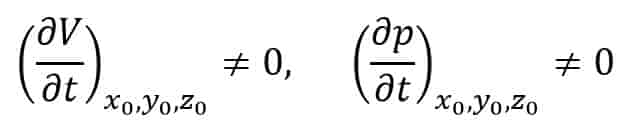
2. Uniform and Non-uniform Flows
Uniform flow is defined as that type of flow in which the velocity at any given time does not change with respect to space (i.e., length of direction of the flow).
Mathematically, for uniform flow, we can write
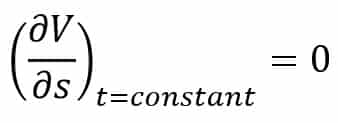
where
∂V = Change of velocity
∂s = Length Of flow in the direction S
Non-uniform flow is that type of flow in which the velocity at any given time changes with respect to space.
Thus, mathematically for non-uniform, we can write
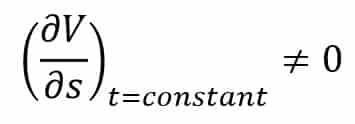
3. Laminar and Turbulent Flows
Laminar flow is defined as that type of flow in which the fluid particles move along well-defined paths or streamlines and all the streamlines are straight and parallel.
Thus the particles move in laminas or layers gliding smoothly over the adjacent layer. This type of flow is also called stream-line flow or viscous flow.
Turbulent flow is that type of flow in which the fluid particles move in a Zig-zag way. Due to the movement of fluid particles in a zig-zag way, eddies formation takes place which is responsible for high energy loss.
For a pipe flow, the type Of flow is determined by a non-dimensional number VD/v called the Reynold number.
Reynold number = VD/v
where
D = Diameter Of pipe
V = Mean velocity of flow in pipe
v = Kinematic viscosity of the fluid
If the Reynold number is less than 2000, the flow is called laminar.
If the Reynold number is more than 4000, it is called turbulent flow.
If the Reynold number lies between 2000 and 4000, the flow may be laminar or turbulent.
4. Compressible and Incompressible Flows
Compressible flow is that type of flow in which the density of the fluid changes from point to point.
In other words, the compressible flow can be defined as the density (ρ) is not constant for the fluid.
Thus, mathematically, for compressible flow
ρ ≠ Constant
Incompressible flow is that type of flow in which the density is constant for the fluid flow. Liquids are generally incompressible while gases are compressible.
Mathematically, for incompressible flow
ρ = Constant
5. Rotational and Irrotational Flows
Rotational flow is that type of flow in which the fluid particles while flowing along streamlines, also rotate about their own axis. And if the fluid particles while flowing along streamlines, do not rotate about their own axis then that type of flow is called irrotational flow.
6. One-Dimensional, Two-Dimensional and Three-Dimensional Flows
One-dimensional flow is that of flow in which the flow parameter such as velocity is a function of time and one space co-ordinate only, say x.
For a steady one-dimensional flow, the velocity is a function of one-space-co-ordinate only. The variation of velocities in the Other two mutually perpendicular directions is assumed negligible.
Hence mathematically, for one-dimensional flow,
u = f(x), v = 0 and w = 0
where u, v and w are velocity components in x, y and z directions respectively.
Two-dimensional flow is that type of flow in which the is a function of time and two rectangular space coordinates say x and y.
For a steady two-dimensional flow, the velocity is a function of two space coordinates only. The variation or velocity in the third direction is negligible.
Thus, mathematically for two-dimensional flow
u = f1(x, y), v = f2(x, y) and w = 0
Three-dimensional flow is that type of flow in Which the velocity is a function of time and three mutually perpendicular directions.
But for a steady three-dimensional flow, the fluid parameters are functions of three space coordinates (x, y and z) Only.
Thus, mathematically, for three-dimensional flow
u = f1(x, y, z), v = f2(x, y, z) and w = f3(x, y, z)
These are all 6 different types of fluid flows which help us determine the velocity and the acceleration of fluid flow in the next articles.
Now we know the types of flow, but how do we can calculate the amount of flow discharge through the pipe if we already know the velocity
Rate of Flow discharge (Q)
It is defined as the quantity of fluid flowing per second through a section of a pipe or a channel. For an incompressible fluid (or liquid) the rate of flow or discharge is expressed as the volume of fluid flowing across the section per second.
For compressible fluids, the rate of flow is usually expressed as the weight of fluid flowing across the section.
- For liquids, the units of Q are m3/s or litres/s
- For gases, the units of Q are kgf/s or Newton/s
Consider a liquid flowing through a pipe, Then discharge through the pipe is
Q = A × V
Where
A = Cross-sectional area Of pipe
V = Average velocity of fluid across the section
Continuity Equation
From the *law of conservation of mass, we can write the continuity equation.
*Law of conservation of mass: Law of conservation of mass states that the mass can neither be created nor destroyed but is transformed from one form to another.
As we stated the equation based on the law of conservation of mass is called the continuity equation. For a fluid flowing through a pipe at all the cross-sections, the quantity of the fluid per second is constant.
Consider two cross-sections of a pipe as shown in the following figure
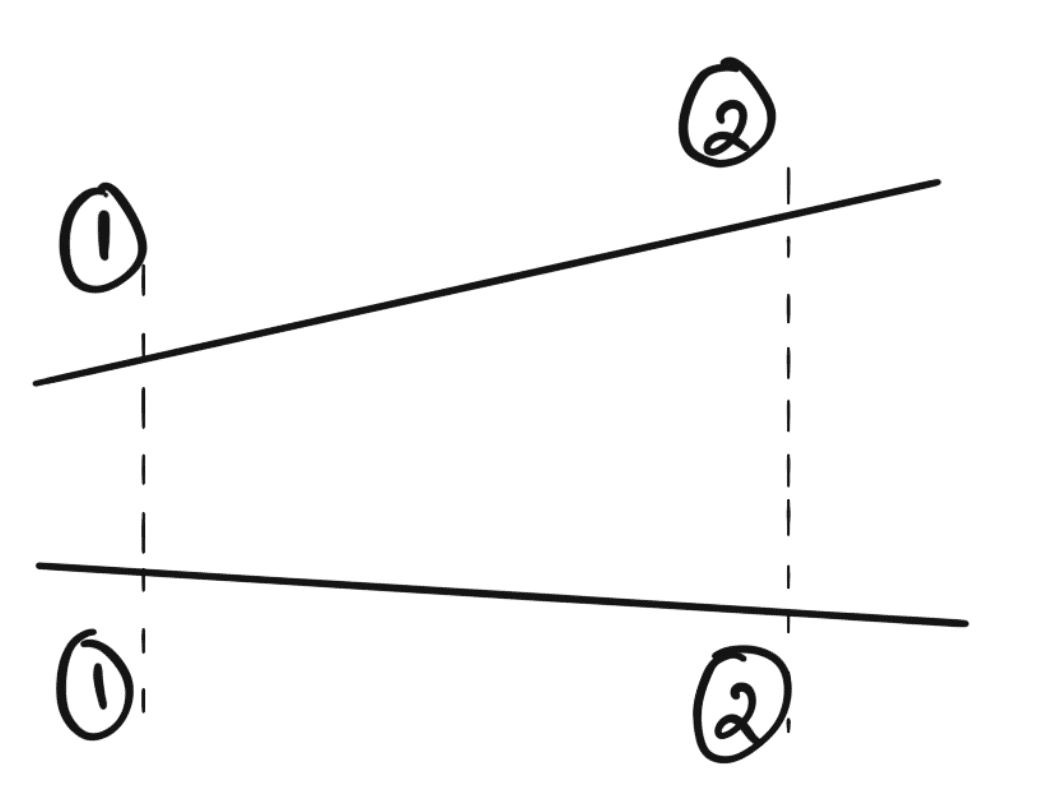
Let
V1 = Average velocity at cross-section 1-1
ρ1 = Density at section 1-1
A1 = Area of pipe at section 1-1
and V2, ρ2 A2, are corresponding values in section, 2-2.
The rate of flow at section 1-1 = ρ1 A1V1
The rate of flow at section 2-2 = ρ2 A2V2
According to the law of conservation of mass from the above
Rate of flow at section 1-1 = Rate of flow at section 2-2
The above equation is applicable to compressible as well as incompressible fluids and is called Continuity Equation.
If the fluid is incompressible, then ρ1 = ρ2, and the above continuity equation reduces as follows
A1V1 = A2V2
Read more on the Continuity Equation in three dimensions and also in the Polar coordinates
Let us solve an example problem to find the fluid discharge through a pipe with help of the above continuity equation.
Problem Statement: The diameters of the pipe ar the sections 1 and 2 are 10cm and 15cm respectively. Find the discharge through the pipe if the velocity of water flowing through the pipe at section 1 is 5 m/s. Determine also the velocity in section 2.
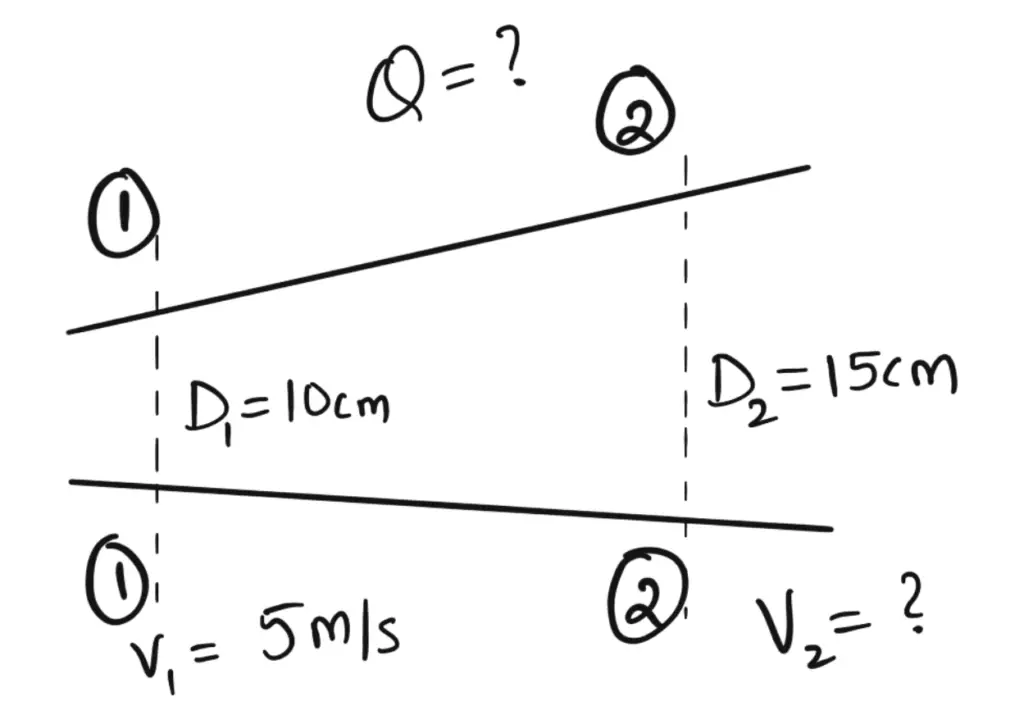
Solution:
Given that
Section 1 pipe diameter D1 = 10cm = 0.1m
cross sectional area A1 = (ℼ/4) (D1)2 = 0.007854m2
Velocity of flow at section 1 V1 = 5m/s
Section 2 pipe diameter D2 = 15cm = 0.15m
cross sectional area A2 = (ℼ/4) (D1)2 = 0.01767m2
Discharge (Q) thought the pipe is
Q = A1 × V1
Q = 0.007854 × 5
Q = 0.03927 m3/s
Velocity at the section 2 (V2)
We know from the above continuity equation
A1V1 = A2V2
0.007854 × 5 = 0.01767 × V2
V2 = 2.22m/s
This is how you can calculate the discharge or velocity of any fluid if you know the sufficient inputs as illustrated above.
Can you solve an example problem on this same topic?
Exercise Problem: A 30cm diameter pipe conveying water branches into IWO pipes Of diameters of 20cm and 15cm respectively. If the average velocity in the 30cm diameter pipe is 2.5 m/s, find the discharge in this pipe. Also, determine the velocity in 15cm pipe if the average velocity in 20cm diameter pipe is 2 m/s.
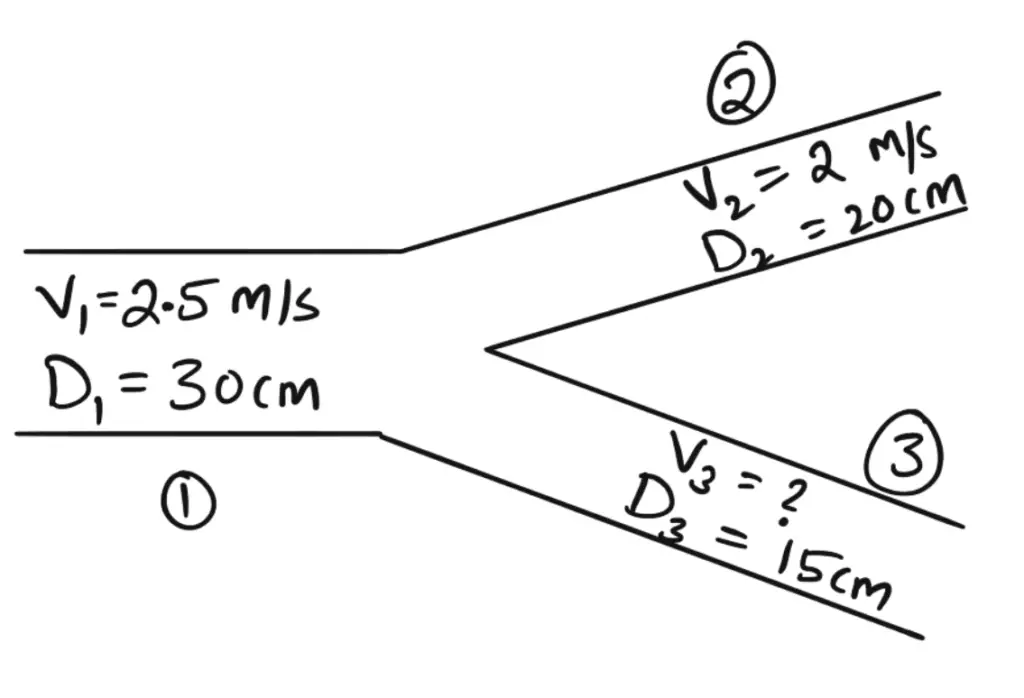
Solve it and let us know the answer in the comment section below. I will help you.
We have been discussing Basic Fluid mechanics topics as follows

Leave a Reply