We have discussed the mechanical properties of engineering materials in the previous articles. Fluids (liquids and gases) are also a very important part of engineering. The branch of science deal with the dynamics and mechanics of fluids called Fluid Mechanics. Let us understand a few important terminologies before we understand the properties of the Fluids in fluid mechanics.
- The study of fluids at rest is called Fluid Statice.
- The study of fluids in motion where pressure forces are not considered is called Fluid Kinematics.
- The study of fluids in motion where pressure forces are also considered for the fluids in motion, that branch of science is called Fluid Dynamics.
Properties of Fluids
In general, the physical properties of Fluids are Density, Viscosity and Surface tension among the other fluid properties. Let us discuss the important properties of Fluids along with Density, Viscosity and surface tension.

Density Or Mass Density
The density or mass of a fluid is defined as the mass of a fluid to its volume. Thus mass per unit volume of a fluid is called density.
lt is denoted by the symbol ρ (rho).
The SI unit’s mass density unit is Kg per cubic metre (kg/m3).
The density of liquids may be considered a constant while gases change with the variation of pressure and temperature.
mathematically, mass density is written as ρ = Mass of fluid ÷ Volume of fluid
The value of the density of water is gm/cm3 or 1000 kg/m3
Specific weight or Weight Density.
Specific weight or weight density of the fluid is the ratio between the weight of a fluid and its volume.
Thus weight per unit volume of a fluid is called weight density and it is denoted by the symbol w.
Thus mathematically,
w = Weight of fluid ÷ Volume of fluid
w = (Mass of fluid × Acceleration but to gravity) ÷ Volume of fluid
w = (Mass of fluid ÷ Volume of fluid) × g
w = ρ×g
The SI units for the specific weight density is Newton /m3
The value of specific weight density (w) for water is 9.811000 Newton /m3 in SI units.
Specific Volume
The specific volume of a fluid is defined as the volume of fluid occupied by a unit mass or volume per unit mass of fluid called specific volume.
Mathematically, it is expressed as follows
Specific volume = Volume of fluid ÷ Mass of fluid
The above expression can be written as = 1 / (Mass of fluid ÷ Volume of fluid)
Specific Volume = 1/ρ
Thus the specific volume is the reciprocal of mass density.
The SI units for Specific Volume is m3/kg.
Specific volume is commonly applied to gases.
Specific Gravity
Specific gravity is defined as the ratio of weight density(or density) of fluid to the weight density (or density) of a standard fluid.
For liquids, the standard fluid is taken water and for gases, the standard fluid is taken air.
Specific gravity is also called relative density.
It is a dimensionless quantity and is denoted by the symbol S.
Mathematically,
S (for liquids) = Weight density (density) of liquid ÷ Weight Density (density) of water
S (for gases) = Weight density (density) of gas ÷ Weight density (density) of air
Thus Weight density of a liquid = S × Weight density of water = S × 1000 × 9.81 N/m3
The density of a liquid = S × Density of water = S × 1000 kg/m3.
If the specific gravity of fluid is known, then the density of the fluid will be equal to the specific gravity of fluid multiplied by the density of water. For example, the specific gravity of mercury is 13.6, hence the density of mercury =13.6 ×1000= 13600 kg/m3
How to calculate the specific weight, density and specific gravity of any liquid?
Example Problem 1
Calculate the specific weight, density and specific gravity of a liquid which weighs 7N.
Answer:
Volume =1 litre =1/1000 m3
(i) Specific weight(w) = Weight ÷ volume = 7N ÷ [1/1000]m3 = 7000 N/m3.
(ii) Density (ρ) = w / g = 7000 ÷ 9.81 kg/m3 = 731.5 kg /m3 .
(iii) Specific gravity = density of liquid / density of water = 731.5 / 1000 = 0.731.5.
Example Problem 2
Calculate the density , specific weight and weight of one litre of specific gravity = 0.7
Answer:
Given data : Volume = 1 litre = 1×1000 cm3 = 1000 cm3 = 0.001 m3
Specific gravity S = 0.7
(i) Density (ρ) = S × Density of water = S ×1000 kg / m3 = 0.7 ×1000 = 700 kg/ m3 .
(ii) Specific weight (w) = ρ×g = 700×9.81 N/m3 = 6867 N/m3 .
(iii) Weight (W) = Specifi weight(w) × Volume of fluid
W = 6867 × 0.001 = 6.867 N.
Viscosity
Viscosity is defined as the property of a fluid which offers resistance to the movement of one layer of fluid over another adjacent layer of the fluid.
When two layers of fluid, are a distance dy apart, move one over the other at different velocities say u and u + du as shown in the below figure, the viscosity together with relative velocity causes shear stress acting between the fluid layers.
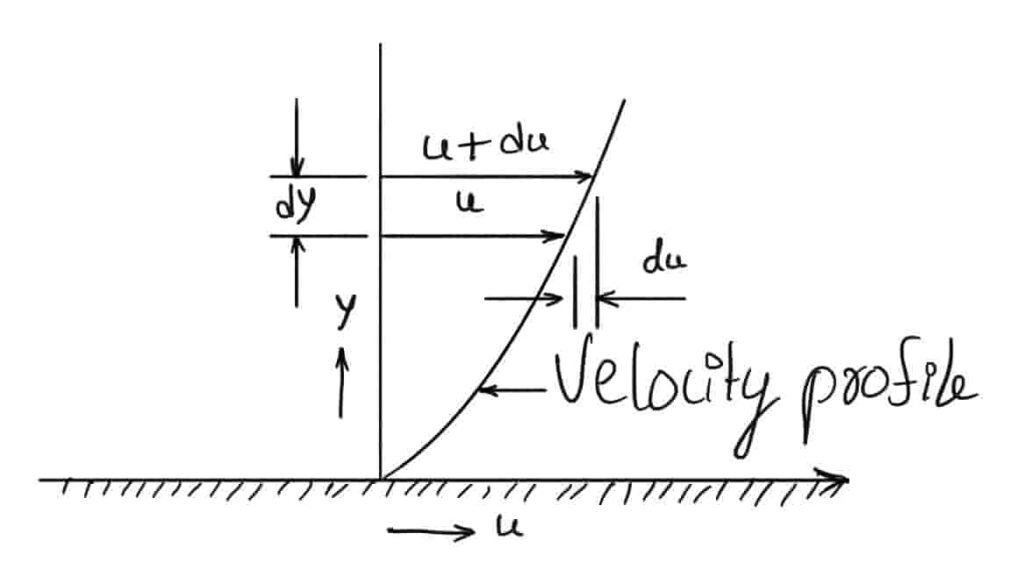
The top layer causes shear stress on the adjacent lower layer while the lower layer causes another stress on the adjacent top layer.
This shear stress is proportional to the velocity change rate with respect to y. It is denoted by a symbol called Tau.
Mathematically,
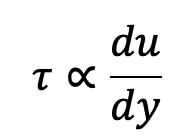
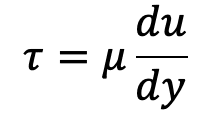
Where µ (called mu) is the constant of proportionality and is known as the coefficient of dynamic viscosity or only viscosity.
du/dy represents the rate of shear strain or rate of shear deformation or velocity gradient.
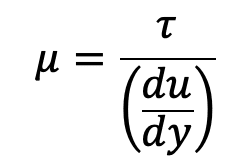
Thus viscosity is also defined as the shear required to produce a unit rate of shear strain.
The units of viscosity are obtained by putting the dimensions of the quantities in the above equation
µ = Shear stress/change of velocity /change of distance
µ = Force × Time ÷ (length)2
In the MKS system, force is represented by kgf and length by the metre (m),
In the CGS system, force is represented by dyne and length by cm
In the SI system force is represented by Newton (N) and length by the metre (m).
MKS unit of viscosity= kgf-sec/m2
CGS unit of viscosity= dyne-sec/cm2
In the above expression, N/m2 is also known as Pascal which is represented by Pa.
Hence N/m2 = Pa = Pascal
SI unit of viscosity = Ns/m2 = Pas.
SI unit of viscosity = Newton-sec/m2 = Ns/m2
The unit of viscosity in CGS is also called Poise which is equal to dyne-sec/cm2
Surface Tension
Surface tension is defined as the tensile force acting on the surface of a liquid in contact with a gas or
on the surface between two immiscible liquids such that the contact surface behaves like a membrane
under tension.
The magnitude of this force per unit length of the free surface will have the same value as the surface energy per unit area.
It is denoted by the Greek letter σ (called sigma).
In MKS units, it is expressed as kgf/m
In SI units as N/m
Conclusion
We have discussed the properties of Fluids for the level of very basic understanding. In the next articles, we have discussed the Viscosity and Surface tension in a detailed manner. Let us know what you think about this article in the comment section below.

Leave a Reply