In Fluid Mechanics, Surface tension is one of the important physical properties of fluid among Density and Viscosity. Surface tension is defined as the tensile force acting on the surface of a liquid in contact with a gas or on the surface between two immiscible liquids such that the contact surface behaves like a membrane under tension. Let us discuss the surface tension of fluid in detail along with the surface tension phenomenon called the Capillarity.

Surface Tension
Surface tension is defined as the tensile force acting on the surface of a liquid in contact with a gas or on the surface between two immiscible liquids such that the contact surface behaves like a membrane under tension.
The magnitude of this force per unit length of the free surface will have the same value as the surface energy per unit area.
It is denoted by the Greek letter σ (called sigma).
In MKS units, it is expressed as kgf/m
In SI units as N/m
The Surface Tension phenomenon will be explained in the following figure.
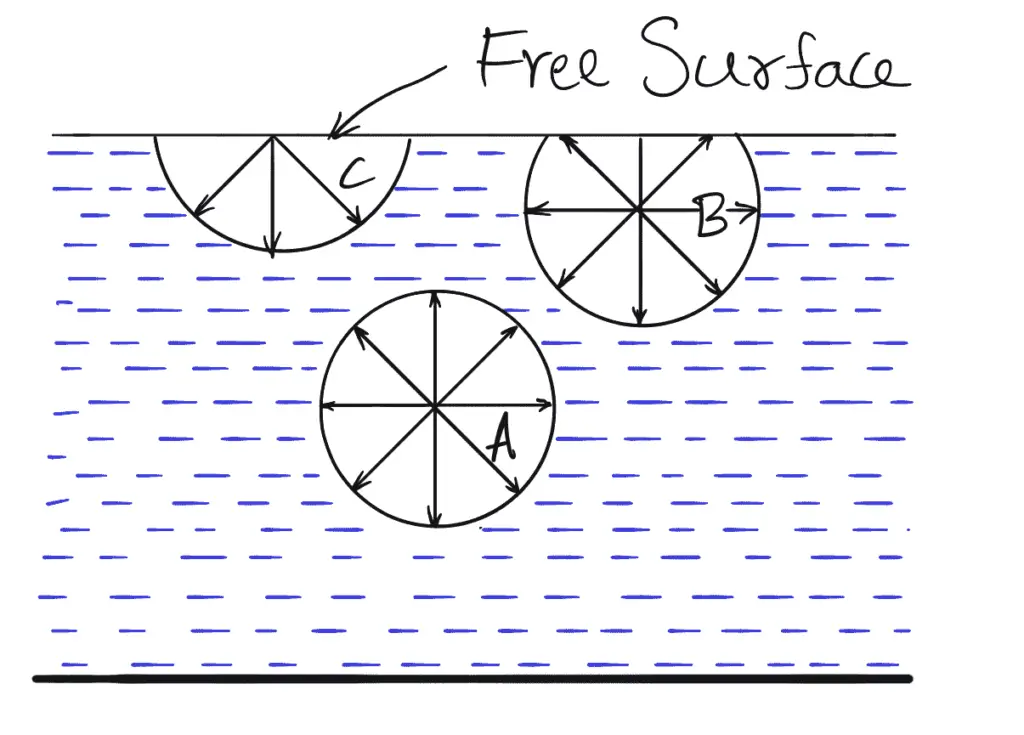
- Let us consider three molecules A, B, and C of a liquid in a mass of liquid.
- Molecule A is attracted in all directions equally by the surrounding molecules of the liquid.
- Thus the resultant force acting on molecule A is zero.
- But molecule B, which is situated near the free surface, is acted upon by upward and downward forces which are unbalanced.
- Thus a net resultant force on molecule B is acting in the downward direction.
- The molecule C, situated on the free surface of the liquid, does experience a resultant downward force.
- All the molecules on the free surface experience a downward force.
- Thus the free surface of the Tupuid acts like a very thin film under the tension of the surface of the liquid act as though it is an elastic membrane under tension.
Surface Tension on Liquid Droplet
Consider a small spherical droplet of a liquid of radius ‘r‘.

On the entire surface of the droplet, the tensile force due to surface tension will be acting)
Let
σ = Surface tension of the liquid
ρ= Pressure intensity inside the droplet (in excess of the outside pressure intensity)
d = Diameter of the droplet.
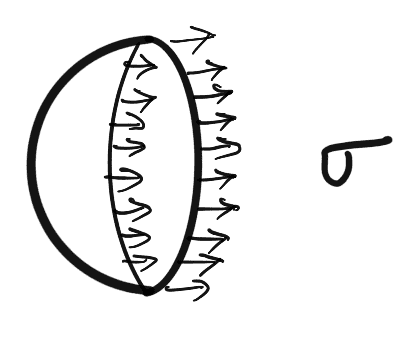
Let the droplet is cut into two halves.
The forces acting on one half (say left half) will be
- Tensile force due to surface tension acting around the circumference of the cut portion as shown in figure (b) and this is equal to = σ x Circumference
Tensile force =σ × πd - Pressure forces on the area = (π/4) × d2 = p × (π/4) × d2 as shown in Figure (c).
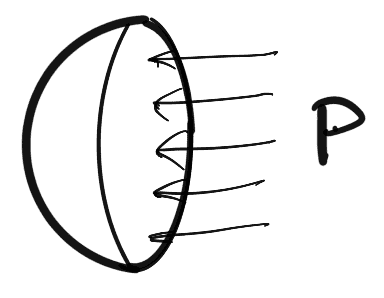
These two forces will be equal and opposite under equilibrium conditions, i.e.,
p × π/4 × d2 = σ × πd
p = σ × πd/(π/4) × d2
p = (4σ)/d
The above equation shows that with the decrease in the diameter of the droplet, pressure intensity inside the droplet increases.
Surface Tension on a Hollow Bubble
A hollow bubble like a soap bubble in the air has two surfaces in contact with the air, one inside and another outside.
Thus two surfaces are subjected to surface tension. In such a case, we have
p × π/4 × d2 = 2 × (σ × πd)
p = 2σπd/π/4 d2
p = 8σ/d
Surface Tension on a Liquid Jet
Consider a liquid jet of diameter “d’ and length ‘L’ as shown in the figure below.
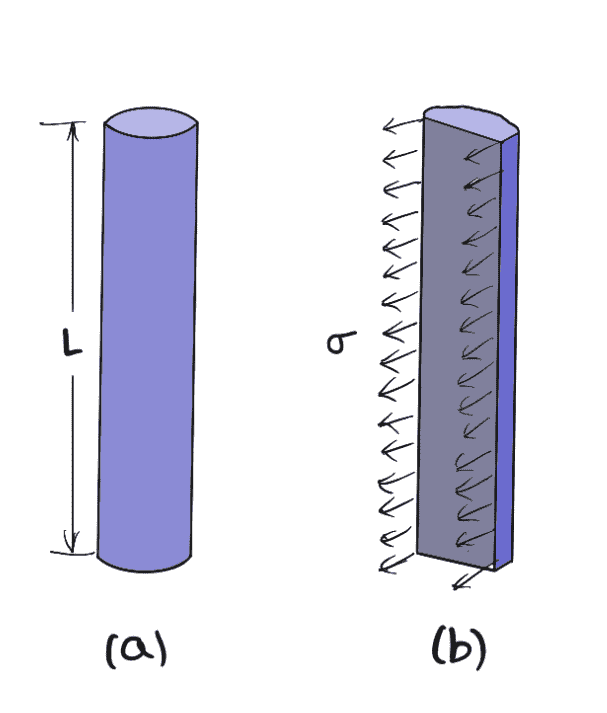
Let
p = Pressure intensity inside the liquid jet above the outside pressure
σ = Surface tension of the liquid
Considering the equilibrium of the semi jet, we have
Force due to pressure = p × area of semi jet = p × L × d
Force due to surface tension = σ × 2L
Equating the forces, we have
p × L × d = σ × 2L
p = (σ × 2L)/ L×d
Example Problems on Surface Tension
Let us solve Some of the example problems on Surface tension of water and Soap bubble
Problem Statement 1: The surface tension of water in contact with air at 20°C is 0.0725 N/m. The pressure inside a droplet of water is to be 0.02 N/cm2 greater than the outside pressure. Calculate the diameter of the droplet of water.
Answer:
Given data
Surface tension σ = 0.0725 N/m
Pressure intensity, p in excess of outside pressure is p = 0.02 N/cm2 = 0.02 × 104 N/m2
d = diameter of the droplet
Using equation from above p = (4σ)/d
0.02 x 104 = 4 × 0.0725/d
d = 4 × 0.0725/0.02 x 104
d = 0.00145 m
d = 0.00145 × 1000
d = 1.45 mm
Problem Statement 2: Find the surface tension in a soap bubble of 40 mm diameter when the inside pressure is 2.5 N/m2 above atmospheric pressure.
Answer:
Given data
Diamter of bubble d= 40 mm = 40 × 10-3 m
Pressure in excess of outside, p = 2.5 N/m2
For a soap bubble, using equation p = 8σd we get
2.5 = 8σ/(40 x10-3)
σ = (2.5 × 40 × 10-3)/8N/m
σ = 0.0125 N/m
Problem Statement 3: The pressure outside the droplet of water of diameter 0.04 mm is 10.32 N/cm2 (atmospheric pressure). Calculate the pressure within the droplet if surface tension is given as 0.0725 N/m of water.
Answer:
Given data
Diameter of droplet d = 0.04 mm = 0.04 × 10-3 m
Pressure outside the droplet poutside = 10.32 N/cm2= 10.32 × 104 N/m2
Surface tension σ = 0.0725 N/m
The pressure inside the droplet, in excess of outside pressure is given by following equation
p = 4σ/d
p = (4 × 0.0725)/(0.04 × 10-3)
p = 7250 N/m2
p = 7250 N/104cm2
p = 0.725 N/cm2
Pressure inside the droplet = p + Pressure outside the droplet
p = 0.725 + 10.32
p = 11.045 N/cm2
Capillarity
Capillarity is defined as a phenomenon of the rise or fall of a liquid surface in a small tube relative to the adjacent general level of liquid when the tube is held vertically in the liquid.
The rise of the liquid surface is known as capillary rise while the fall of the liquid surface is known as capillary depression.
It is expressed in terms of cm or mm of liquid Its value depends upon the specific weight of the liquid, the diameter of the tube and the surface tension of the liquid.
Expression for Capillary Rise
Consider a glass tube of small diameter ‘d’ opened at both ends and is inserted in a liquid, say water.
The liquid will rise in the tube above the level of the liquid.
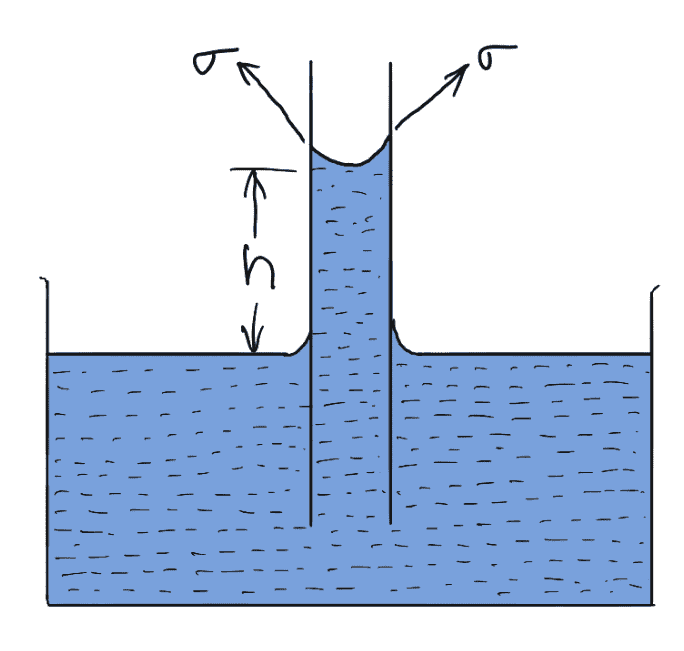
Let h = the height of the liquid in the tube.
Under a state of equilibrium, the weight of liquid of height is balanced by the force at the surface of equilibrium, the liquid in the tube. But the force at the surface of the liquid in the tube Is due to surface tension.
Let
σ= Surface tension of the liquid
θ= Angle of contact between liquid and glass tube
ρ = Density of liquid
The weight of liquid of height h in the tube = (Area of tube × h) × ρ × g
= π/4 d2×h× ρ×g
The vertical component of the surface tensile force
= (σ× Circumferènce) × cosθ
= σ × πd × cosθ
For Equllibrium, equating the above two equation, we get
π/4 d2×h× ρ×g = σ × πd × cosθ
h = (σ × πd× cosθ)/π/4 d2×ρ×g
h = (4σcosθ)/ρ×g×d
The value of θ between water and the clean glass tube is approximately equal to zero and hence cosθ is
equal to unity.
Then rise of water is given by
h = 4σ/ρ×g×d
Expression for Capillary Fall
If the glass tube is dipped in mercury, the mercury level in the tube will be lower than the general level of the outside liquid as shown in the figure below.
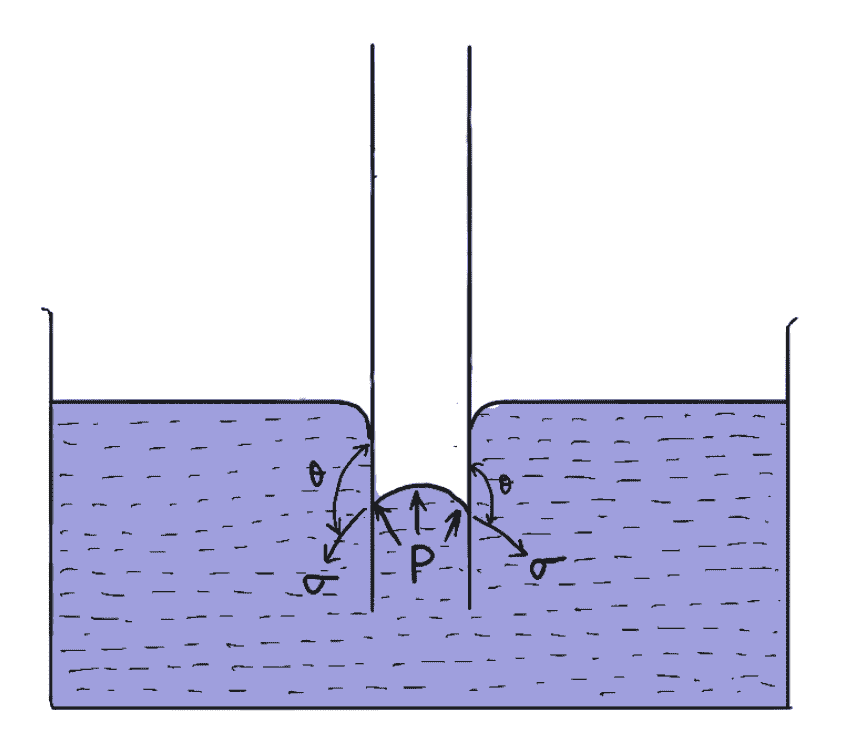
Let h = Height of depression in a tube
Then in equilibrium, two forces are acting on the mercury inside the tube.
The first one is due to surface tension acting in the downward direction and is equal to σ×πd× cosθ
The second force is due to the hydrostatic force acting upward and is equal to. the intensity of pressure at a depth h x Area
= p×π/4 d2
= ρgh × (π/4) d2
Equating the two equations, we get
σ × πd × cosθ = ρgh × π/4 d2
h = 4σ cosθ/ρgd
The value of θ for mercury and glass tube is 128°
Example Problems on Capillarity
Problem statement 4: Calculate the capillary rise in a glass tube of 2.5 mm diameter when immersed vertically in (a) water and (b) mercury. Take surface tensions σ = 0.0725 N/m for water and σ = 0.52 N/m for mercury in contact with air. The specific gravity for mercury is given as 13.6 and the angle of contact =130°.
Answer:
Diameter of the tube d = 2.5 mm = 2.5x 10-3 m
Surface tension, o for water = 0.0725 N/m
σ for mercury = 0.52 N/m
Specific gravity of mercury = 13.6
Density = 13.6 ×1000kg/m3
(a) Capillary rise for water (θ = 0°)
Using equation h = 4σ/ρ×g×d we get
h = 4×0.0725/1000×9.81×2.5×10-3
h = 0.0118m
h = 1.81cm
(b) For Mercury
The angle of contact between mercury and glass tube,θ = 130°
The equation we know for Height of depression in a tube
h = 4σ cosθ/ρ×g×d
h = (4 × 0.52 × cos130°) / (13.6 × 1000 × 9.81 × 2.5×10-3)
h =- 0.004m
h = -0.4cm
The negative sign indicates capillary depression.
Conclusion
We have discussed what is the surface tension of fluid and capillarity of rice and the fall of fluid with water and mercury. We have discussed how we can calculate the surface tension of a water and soap bubble, and how to calculate the capillarity of rice and capillary fall of fluid. Let us know what do you think about this in the comment section below.

Leave a Reply