In Fluid Mechanics, Viscosity is defined as the property of a fluid that offers resistance to the movement of one layer of fluid over another adjacent layer of the fluid. We have discussed the different physical properties of Fluids in the previous article. In this article, we will discuss the Viscosity of fluid and the derivation for the units of Viscosity, kinematic viscosity, and newton’s law of Viscosity.

In general, the physical properties of Fluids are Density, Viscosity and Surface tension among the other fluid properties.
The density or mass of a fluid is defined as the mass of a fluid to its volume.
Surface tension is defined as the tensile force acting on the surface of a liquid in contact with a gas or
on the surface between two immiscible liquids such that the contact surface behaves like a membrane
under tension.
Viscosity of a Fluid
Viscosity is defined as the property of a fluid that offers resistance to the movement of one layer of fluid over another adjacent layer of the fluid.
When two layers of fluid, are a distance dy apart, move one over the other at different velocities say u and u + du as shown in the below figure, the viscosity together with relative velocity causes shear stress acting between the fluid layers.
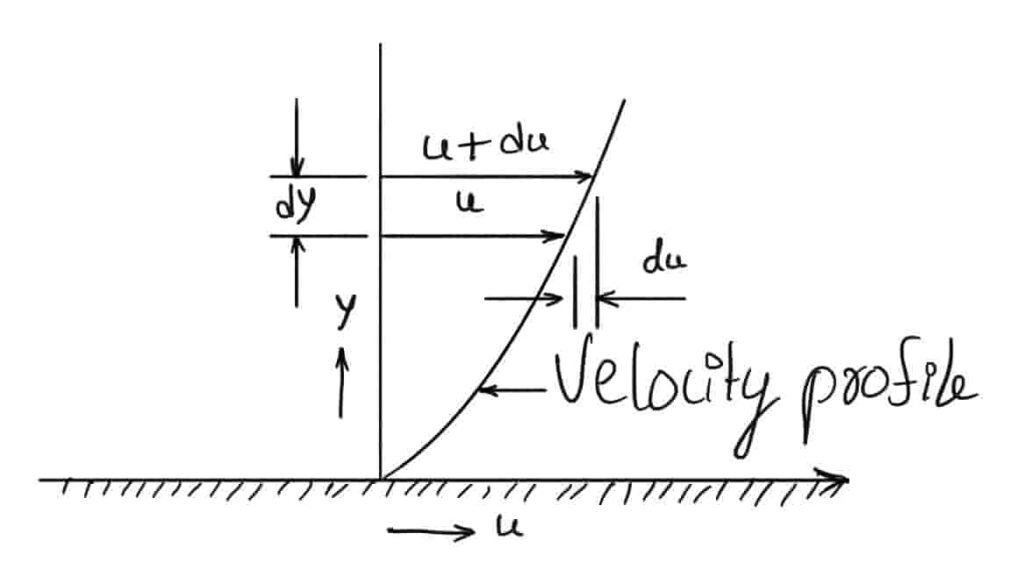
The top layer causes shear stress on the adjacent lower layer while the lower layer causes another stress on the adjacent top layer.
This shear stress is proportional to the velocity change rate with respect to y. It is denoted by a symbol called Tau.
Mathematically,
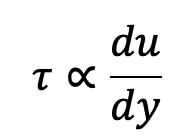
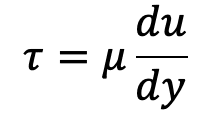
Where µ (called mu) is the constant of proportionality and is known as the coefficient of dynamic viscosity or only viscosity.
du/dy represents the rate of shear strain or rate of shear deformation or velocity gradient.
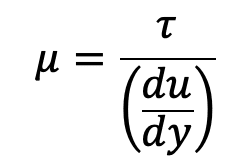
Thus viscosity is also defined as the shear required to produce a unit rate of shear strain.
Units of Viscosity
the units of viscosity are obtained by putting the dimensions of the quantities in the equation given above.

In the MKS system, force is represented by kgf and length by the metre (m).
In the CGS system, force is represented by dyne and length by cm.
In the SI system force is represented by Newton (N) and length by the metre (m).
MKS unit of viscosity = kgf-sec/m2
CGS unit of viscosity = dyne-sec/cm2
In the above expression, N/m2 is also known as Pascal which is represented by Pa.
Hence N/m2 = Pa = Pascal
SI unit of viscosity = Ns/m2 = Pascal
SI unit of viscosity = Newton-sec/m2 = Ns/m2
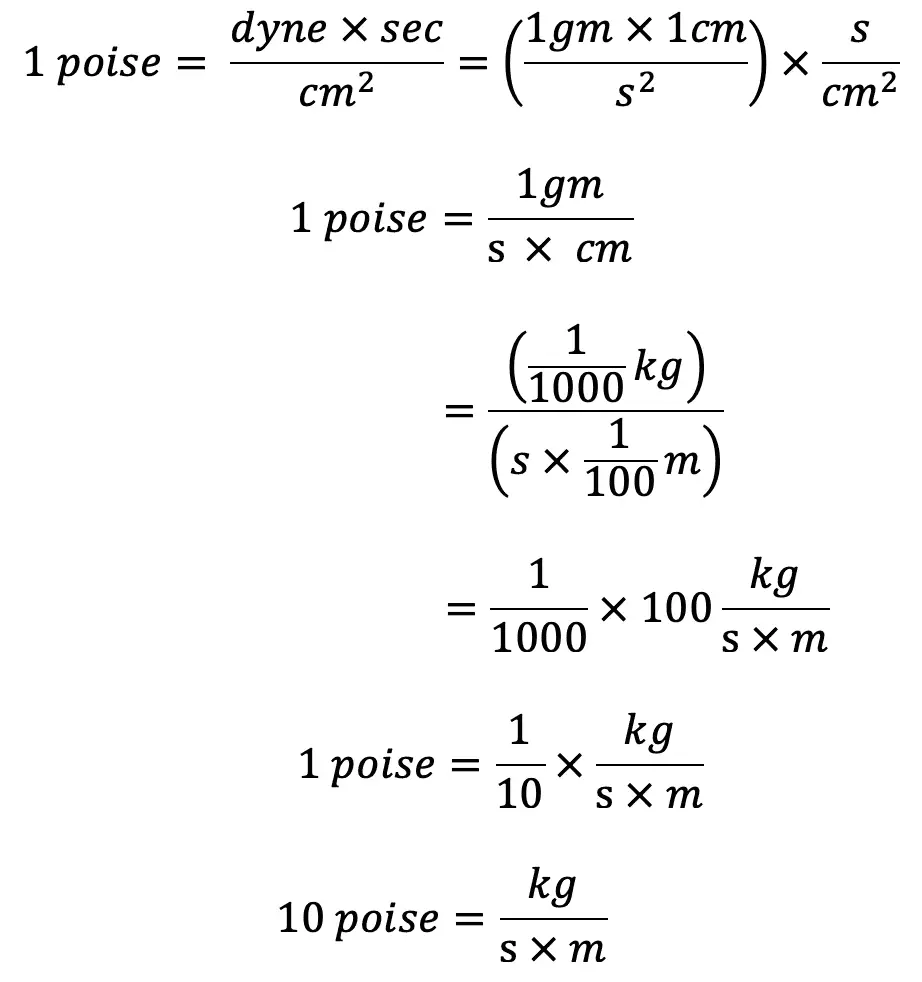
The unit of viscosity in CGS is also called Poise which is equal to dyne-sec/cm2
The Numerical Conversion of the unit of Viscosity from MKS unit to CGS unit:
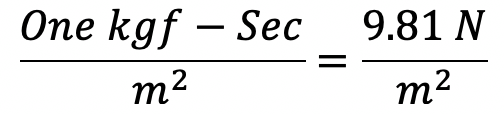
(∴1 kgf = 9.81 Newton)
But one Newton = one kg (mass) x one (m/sec2) (acceleration)
1 Newton = [(1000 gm) x (100 cm)] / Sec2
1 Newton = 1000 × 100 gm-cm/sec2
1 Newton = 1000 x 100 dyne. ( ∴ 1 dyne = gm-cm/sec2)
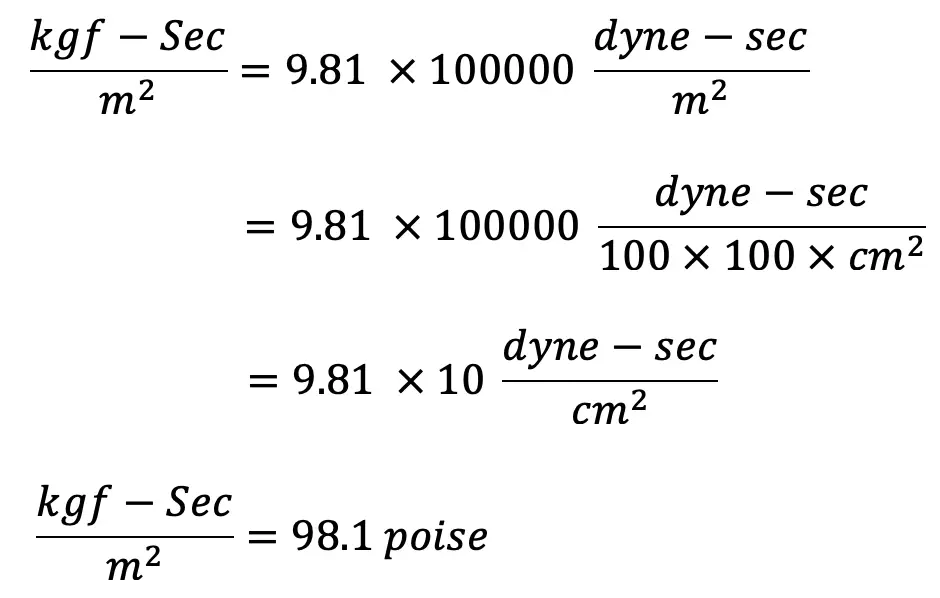
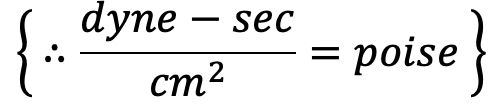
Thus for solving numerical problems if the viscosity is given in poise (CGS unit) it must be divided by 98.1 to get its equivalent numerical value in MKS.
Further,
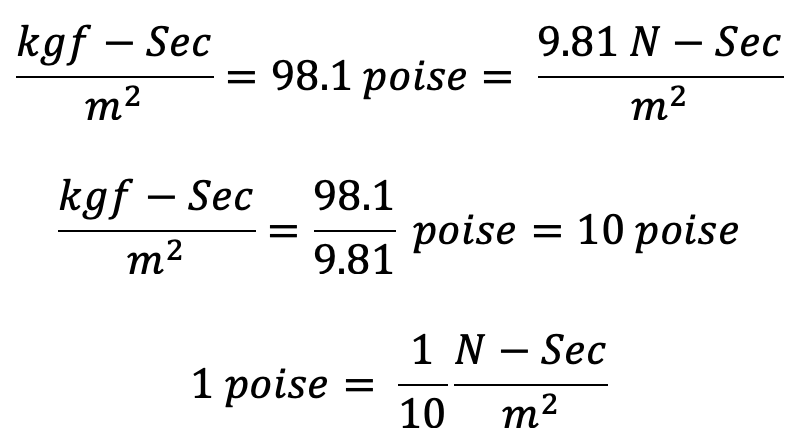
Alternate Method
Important Note:
(i) In SI units second is represented by ‘s” and not by “sec”.
(ii) If viscosity is given in poise. it must be divided by 10 to get its equivalent numerical value in SI units.
Sometimes a unit of viscosity as centipoise is used where 1 centipoise = 1/100 poise (or) 1 cP = 1/100 P
(cP = Centipoise, P = Poise)
The viscosity of water at 20° C is 0.01 poise or 1.0 centipoise.
Kinematic Viscosity
It is defined as the ratio between the dynamic viscosity and density of the fluid.
It is denoted by the Greek symbol (ν) called nu’. Thus, mathematically,
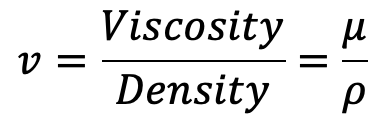
The units of kinematic viscosity are obtained as

In MKS and SI, the unit of kinematic viscosity is metre2/sec or m2/sec
In CGS the unit of kinematic viscosity is cm2/s
In CGS units, kinematic viscosity is also known as stoke.
One stoke = cm2/s = [1/100]2 m2/s = 10-4 m2/s
Centistoke means = 1/100 stoke
Newton’s Law of Viscosity
It states that the shear stress (τ) on a fluid element layer is directly proportional to the rate of shear strain. The constant of proportionality is called the coefficient of viscosity.
Mathematically, it is expressed as given by the above equation or as
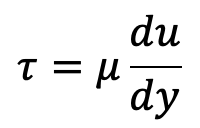
Fluids which obey the above relation are known as Newtonian fluids and the fluids which do not obey the above relation are called Non-newtonian fluids.

Variation of Viscosity with Temperature
Temperature affects viscosity. The viscosity of liquids decreases with the increase of temperature while the viscosity of gases increases with the increase of temperature. This is due to the reason that the viscous forces in a fluid are due to cohesive force and molecular momentum transfer.
In liquids, the cohesive forces predominate the molecular momentum transfer, due to closely packed molecules and with the increase in temperature, the cohesive forces decrease with the result of decreasing viscosity.
But in the case of gases, the cohesive force is small and molecular momentum transfer predominates. With the increase in temperature, molecular momentary transfer increases and hence viscosity increases.
The relation between viscosity and temperature for liquids and gases are:
(i)For liquids
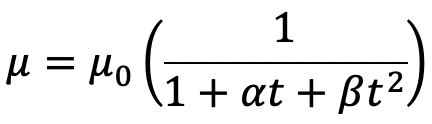
where
µ = Viscosity of liquid at t°C, in poise
µo= Viscosity of liquid at O°C, in poise
α, β = are constants for the liquid
For water
µo = 1.79 x 10-3 poise
α = 0.03368
β = 0.000221
The above equation shows that with the increase in temperature, the viscosity decreases.
(ii) For a gas
µ = µo+ αt – βt2
For air
µo = 0.000017
α = 0.000000056
β = 0.1189 x 10-9
The above equation shows that with the increase in temperature, the viscosity increases.
Types of Fluids based on the Viscosity
The fluids may be classified into the following five types :
- Ideal fluid
- Real fluid
- Newtonian fluid
- Non-Newtonian fluid
- Ideal plastic fluid
Let us discuss these types of fluids definitions.
- Ideal Fluid: A fluid, which is incompressible and is having no viscosity, is known as an ideal fluid. Ideal fluid is only an imaginary fluid as all the fluids, which exist, have some viscosity
- Real Fluid: A fluid, which possesses viscosity, is known as real fluid. All the fluids, in actual practice, are real fluids.
- Newtonian Fluid: A real fluid, in which the shear stress is direct and proportional to the rate of shear strain (or velocity gradient), is known as a Newtonian fluid. Water, air, alcohol, glycerol, and thin motor oil are all examples of Newtonian fluids.
- Non-Newtonian Fluid: A real fluid, in which the shear stress is not proportional to the rate of shear strain (or velocity gradient), is known as a Non-Newtonian fluid. In other words, the viscosity of the fluid increases or decreases when shear is applied. Quicksand, putty Paint, Blood, melted butter.
- Ideal Plastic Fluid: A fluid, in which shear stress is more than the yield value and shear stress is
proportional to the rate of shear strain (or velocity gradient), is known as an ideal plastic fluid.
This is all about the Viscosity of Fluid. Let us solve some of the example problems to understand how we can use the above-given relations, equations and unit derivations to determine Shear stress in a viscous fluid.
Example Problems on Viscosity
1. Calculating Shear stress of a Viscous Fluid
Problem Statement: The velocity distribution over a plate is given by u = (2/3) y – y2 in Which u is the velocity in metres per second at a distance of y metre above the plate. Determine the shear stress at y = 0 and y = 0.15m. (Take dynamic viscosity of the fluid as 8.63 poises.)
Answer:
Given velocity distribution u=2/3 y-y2
Let us differentiate w.r.t y on both sides, we get du/dy = 2/3 -2y
[du/dy]at y=0 or [du/dy]y=0 = (2/3) – 2(0) = 2/3 = 0.667
[du/dy]at y=0.15 or [du/dy]y=0.15 = 2/3 -2(0.15) = 0.667-0.03 = 0.367
Value Of µ = 8.63 poise = 8.63/10 Sl units = 0.863 N s/m2
Now shear stress is given by equation
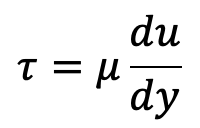
(i) Shear Stress at y = 0 is given by
τ0 = µ (du/dy)y=0
τ0 = 0.863 x 0.667
τ0 = 0.5756 N/m2
(ii) Shear stress at y = 0.15 m is given by
τy=0.15 = µ (du/dy)y=0.15
τy=0.15 = 0.863 x 0.367
τy=0.15 = 0.3167 N/m2
2. Calculating Fluid Viscosity
Problem Statement: A plate, 0.025mm distant from a fixed plate, moves at 60 cm/s and requires a force of 2 N per unit area (2 N/m2) to maintain this speed. Determine the fluid viscosity between the plates.
Answer:
Given data
Distance between plates dy = 0.025mm = 0.025x 10-3m
Velocity of upper plate u = 60 cm/s = 0.6 m/s
Force on the upper plate F = 2.0 N/m2 (This is the value of shear stress i.e., τ )
Let the fluid viscosity between plates is µ Using the equation we have
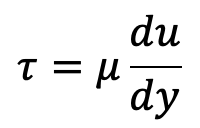
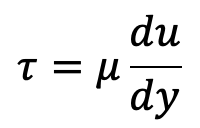
Where
du = Change of velocity = u-0 = u = 0.60m/s
dy = Change of distance = 0.025 x 10-3m
τ = Force per unit area = 2.0N/m2
Substiututing in the above equation we get
2.0 = µ (0.60 / 0.025x 10-3)
µ = 2.0 x (0.025x 10-3 /0.60)
µ = 8.33×10-5 N/m2
µ = 8.33 x 10-5 x10 poise
µ = 8.33 x 10-4 poise
The fluid viscosity between plates µ = 8.33 x 10-4 poise
3. Calculating Kinematic Viscosity
Find the kinematic viscosity of an oil having density of 981 kg/m3. The shear stress ar in oil is 0.2452 N/m2 and the velocity gradient at that point is 0.2 per second.
Answer:
Given data
Mass density ρ = 981 kg/m3
Shear Stress τ = 0.2452 N/m2
Velocity gradient du/dy = 0.2s
We know the equation for shear stress
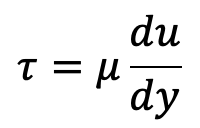
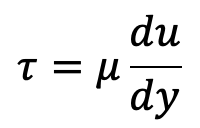
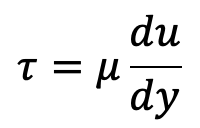
µ = τ (du/dy)
µ = 0.2452 ÷ 0.200 = 1.226 Ns/m2
Kinematic viscosity ν is give by
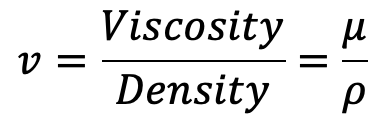
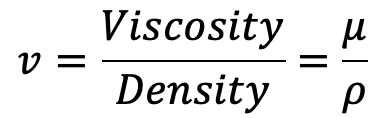
ν = 1.226/981
ν =.125x 10-2 m2/sec
ν = 0.125 x 10-2 x I04cm2/s
ν = 0.125x 102 cm2/s
ν = 12.5 cm2/s
ν = 12.5 stoke
These are some of the example problems that help us to understand how we can calculate shear stress, Fluid viscosity, and kinematic viscosity when the other parameters are known.
Conclusion
We have discussed the Viscosity of fluid and the derivation for the units of Viscosity, kinematic viscosity, and newton’s law of Viscosity. We also solved some example problems to understand how we can calculate the shear stress of a viscous fluid, Fluid viscosity, and kinematic viscosity when the other parameters are known. Let us know what you think about this article in the comment section below.

Leave a Reply