How to calculate Weight Lifted by Hydraulic Jack?

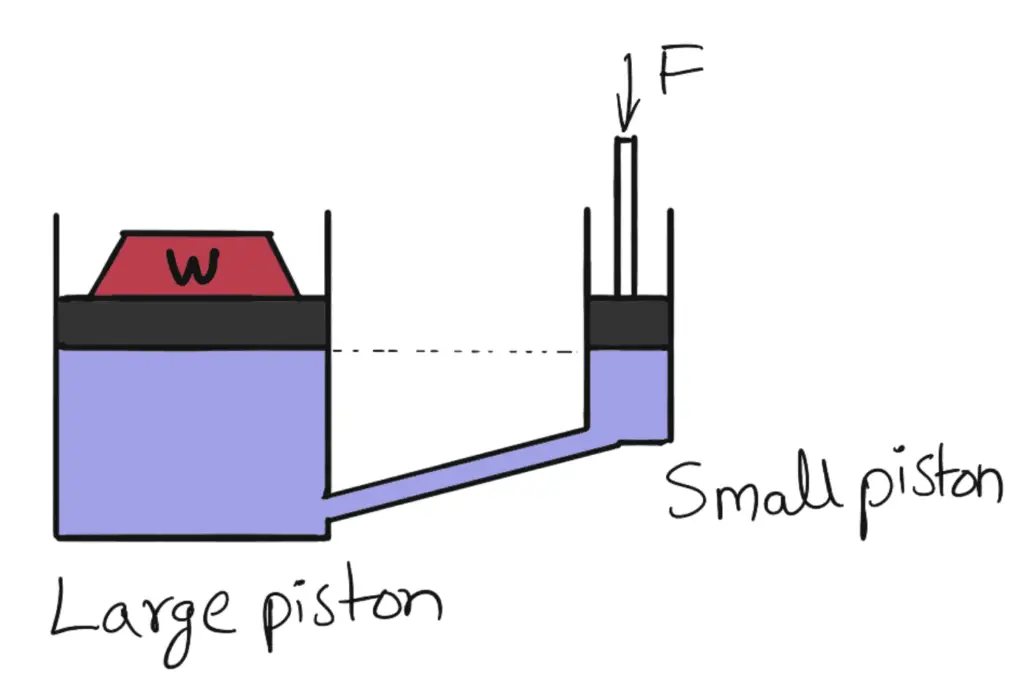
We have discussed Pascal’s Law, Now in this article how we can calculate the weight lifted by Hydraulic Jack with help of Pascal’s Law. Pascal’s Law states that the pressure or intensity of pressure at a point in a static fluid is equal in all directions. Pascal’s law is used in many industrial applications, one of the familiar applications is Hydraulic Jack.

Hydraulic Jack

Hydraulic Jacks are very important and useful devices that are useful to lift heavy loads with very little effort. If you own a car or a 4-wheeler vehicle you must have seen the Hydraulic Jack lift your vehicle from the ground to change the flat tire or any other troubleshooting purpose of your car.

Calculating Weight Lifted by Hydraulic Jack

Problem Statement: The diameters of a small piston and a large piston of a hydraulic jack are 3cm and 10cm respectively. A force of 80 N is applied to the small piston. The density of the liquid in the jack is given as 1000 kg/m.
Find the load lifted by the large piston when
(a) The pistons are at the same level.
(b) The small piston is 40 cm above the large piston.

Answer:

Given Data
Diameter of small piston d = 3 cm
Diameter of Large Piston D = 10cm
Area of small Piston a = π/4 d² = π/4 (3)² = 7.068 cm²
Area of Large Piston A = π/4 D² = π/4 (10)² = 78.54 cm²
Force on small PistonF = 80 N

Let us assume the load lifted = W

(a) When the pistons are at the same level

Pressure intensity formula

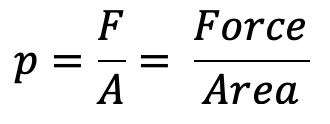
Pressure intensity on the small piston

p_small = F/a
p_small = 80 / 7.068

This is transmitted equally on the large piston.
Pressure intensity on the large piston

p_large = 80/7.068

Force acting on the large piston = Pressure x Area

F = Pressure × Area
F = 80/7.068 × 78.54 N

F = 888.96 N

The Force that should act on the large piston is 888.96 N when we apply a force of 80N on the small piston to maintain the pistons at the same level.

(b) When the small piston is 40 cm above the large piston

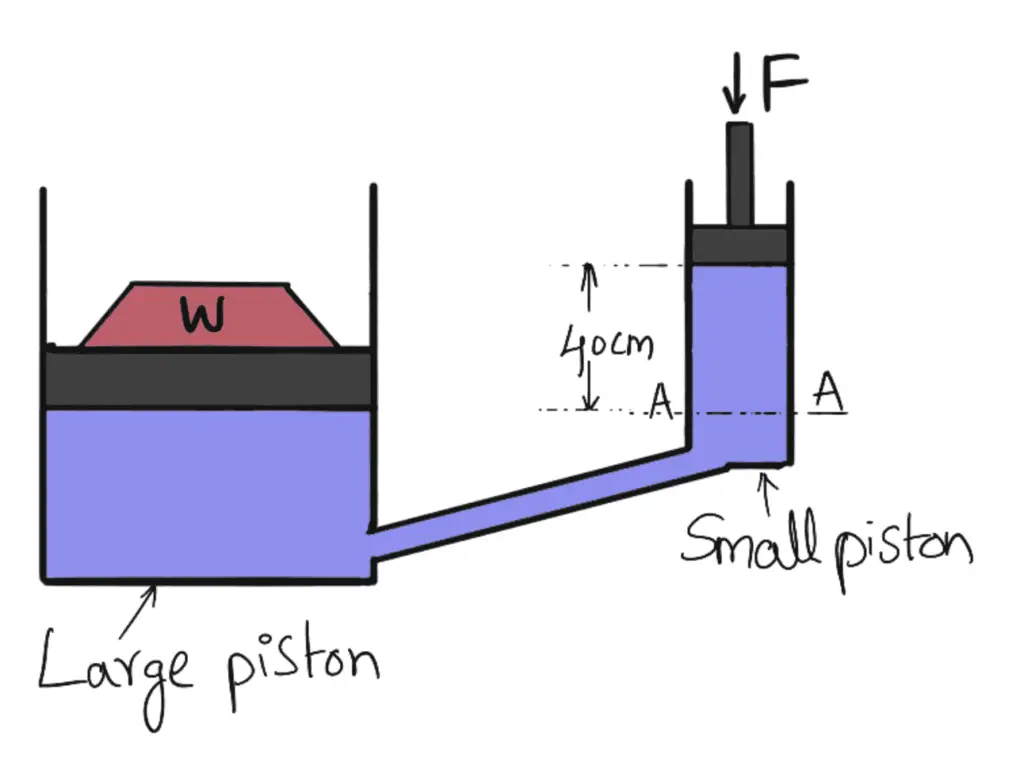
Pressure intensity on the small piston

p_small = F/a
p_small = 80 / 7.068 N/cm²

Pressure intensity at sections A – A

p_section = F/a + Pressure intensity due to height of 40 cm of liquid

But pressure intensity due to 40 cm of liquid

= ρ × g × h
= 1000 × 9.81 × 0.4 N/m²
= 1000 × 9.81 × 0.4 × 10^-4N/cm²
= 0.3924 N/cm²

Pressure intensity at section A – A

p_section = F/a + Pressure intensity due to height of 40 cm of liquid
p_section = 80 / 7.068 + 0.3924 N/cm²
p_section = 11.71 N/cm²

Pressure intensity transmitted to the large piston = 11.71 N/cm²

Force on the large piston = Pressure x Area of the large piston

F =11.71 x A
F = 11.71 x 78.54
F = 919.7 N

The Force that should act on the large piston is 919.7 N when we apply a force of 80N on the small piston to maintain the small piston is 40 cm above the large piston.

Isn’t it simple for you to understand? Can you do a similar problem?

Exercise Problem: The diameters of a small piston and a large piston of a hydraulic jack are 5cm and 15cm respectively. A force of 100 N is applied to the small piston. The density of the liquid in the jack is given as 1000 kg/m.
Find the load lifted by the large piston when
(a) The small piston is 60 cm above the large piston.
(b) The Large piston is 5 cm above the Small piston

Solve it and let us know what did you get in the comment section below.