What is Pascal’s Law? | Pressure Intensity

In Fluid mechanics, Pascal’s Law states that the pressure or intensity of pressure at a point in a static fluid is equal in all directions. So we need to understand the Fluid pressure at any given point. Let us discuss more details on the Fluid pressure at any given point and the Pascals law.

In the previous articles, we have discussed the Physical properties of fluid such as Density, Viscosity and Surface Tension. In this article, we will discuss how the fluid behaves with pressure.

Fluid Pressure at Given a Point

Let us consider a small area dA in a large mass of fluid.

If the fluid is stationary, then the force exerted by the surrounding fluid on the area dA will always be perpendicular to the surface dA.

Let dF be the force acting on the area dA in the normal direction.

Then the ratio of dF/dA is known as the intensity of pressure or simply pressure. This ratio is represented by p.

Hence mathematically we can express the fluid pressure at any given point if the fluid at rest can be written as follows

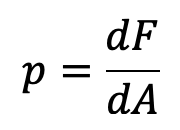
If the force (F) is uniformly distributed over the area (A), then the pressure at any point is given by

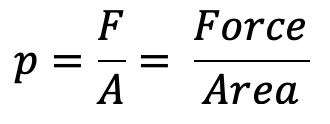
Force or pressure force, F = p x A

The units of pressure are :
In MKS units: kgf/m² and kgf/cm²
In SI units Newton/m² or N/m² and N/mm² (∴ N/m² is known as Pascal and is represented by Pa)

Other commonly used units of pressure are :
kPa = kilo pascal = 1000 N/m²
bar = 100 kPa = 10⁵ N/m²

Now we know what is pressure intensity, Let us discuss the Pascal’s Law

Pascal’s Law

As we mentioned already that Pascal’s law states that the pressure or intensity of pressure at a point
in a static fluid is equal in all directions.

In other words, when an object is immersed in a fluid, it experiences equal pressure on all surfaces. This is also the simple definition of Pascal’s Law.

Let’s prove this…

The fluid element is of very small dimensions i.e., dx, dy and ds.

Consider an arbitrary fluid element of wedge shape in a fluid mass at rest as shown in the following figure.

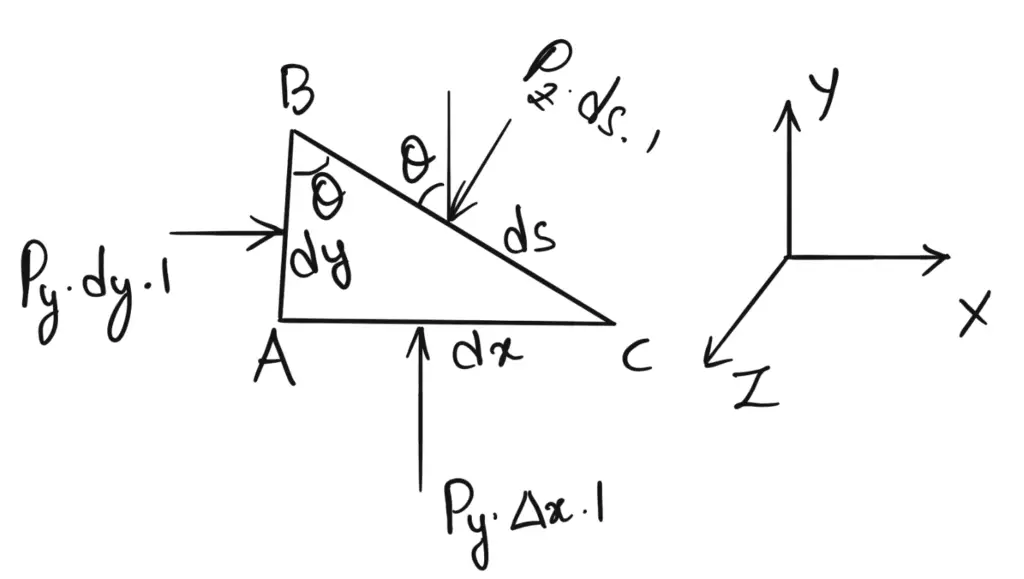
Let the width of the element perpendicular to the plane of paper is unity and p_x, p_y and p_z are the pressures or the intensity of pressures action up on the face AB, AC, and BC respectively.

Let us say ◺ABC = θ

The forces acting on the element are :

1. Pressure forces are normal to the surfaces
2. Weight of element in the vertical direction

Let us take the forces on the faces
Force on the face AB = p_x × Area of face AB = p_x × dy × 1

Similarly force on the face AC = p_y × dx × 1

Force on the face BC = p_z × ds × 1

Weight of element = (Mass of element) × g
= Volume × ρ × g
= [(AB×AC)/2] × 1 × ρ × g

Where ρ = density of fluid

Resolving the forces in x-direction, we have

p_x × dy × 1 – p_z (ds × 1) sin (90°-θ) = 0
p_x × dy × 1 – p_z × ds × cos θ = 0

From the above figure, we can write ds × cos 0 = AB = dy

p_x × dy × 1 – p_z × dy = 0
p_x × dy × 1 = p_z × dy
p_x = p_z …….(a)

Similarly, resolving the forces in y-direction, we get
p_y × dx × 1 – p_z (ds × 1) cos (90°-θ) – [(dx × dy)/2] × 1 × ρ × g = 0
p_y × dx – p_z ds sin θ – (dx dy/2) × ρ × g = 0

From the above figure ds sin θ = dr and also the element is very small and hence weight is negligible.

p_y dx – p_z dx = 0
p_y = p_z ………(b)

From the above equations (a) and (b), we can write that

p_x = p_y = p_z ………(c)

This equation (c) shows that the pressure at any point in the x, y and z directions is equal.

Since the choice of the fluid element was completely arbitrary, it means the pressure at any point
is the same in all directions.

Hence that Pascal states that when an object is immersed in a fluid, it experiences equal pressure on all surfaces.

Calculating Lifting Force in Hydraulics with Pascal’s Law

Let us solve an example problem to find the lifting force with a hydraulic press and a plunger pump.

Problem Statement: A hydraulic press has a ram of 20 cm diameter and a plunger of 3 cm diameter. It is used for lifting a weight of 30 kN. Find the force required at the plunger.

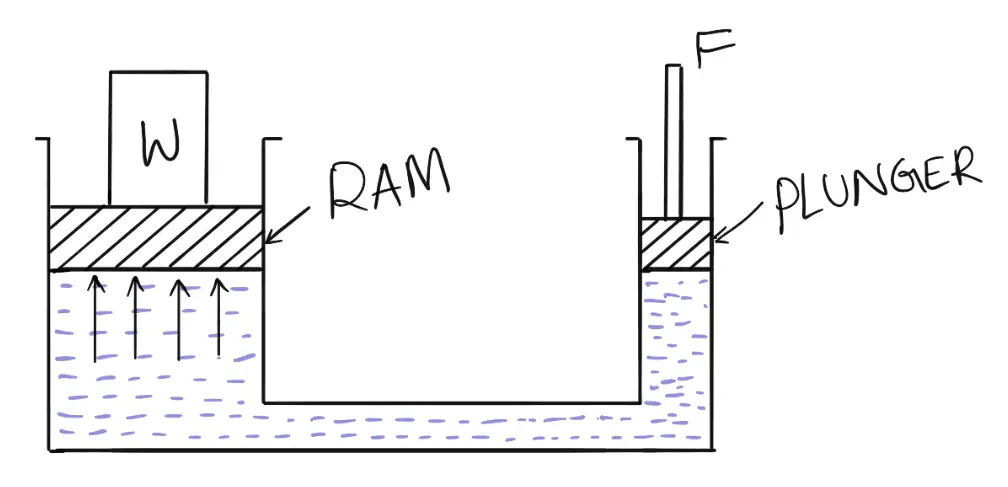
Answer:

Given Data
Diameter of ram D= 20 cm = 0.2 m
Diameter of plunger d = 3 cm = 0.03 m
Area of ram A = π/4 D² = π/4 (0.2)² = 0.0314 m²
Area of plunger a = π/4 d² = π/4 (0.03)² = 7.068 x 10^-4 m²
Weight lifted W= 30 kN = 30 x 1000 N = 30000 N

Pressure intensity developed due to plunger = Force (F) / Area (a)

From Pascal’s law, this pressure is transmitted equally in all directions

Hence pressure transmitted at the ram = F/a

Force acting on ram = Pressure intensity × Area of ram

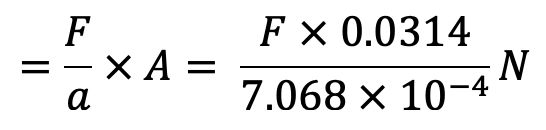
But force acting on ram = Weight lifted = 30000 N

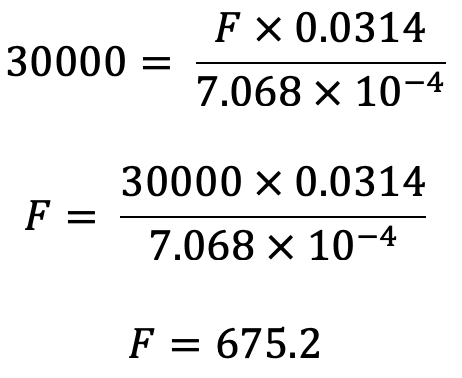
The Force required to lift the weight of 30000 N by the plunger is 675.2 N.

Conclusion

Based on Pascal’s Law many Hydraulic Plunger pumps are working. you can see such hydraulic pumps. We have discussed how we can calculate the weight lifted by the plunger with the hydraulic press. Let us know by solving the following example problem.

Exercise Problem: A hydraulic press has a ram of 30 cm diameter and a plunger of 4.5 cm diameter. Find the weight lifted by the hydraulic press when the force applied at the plunger is 500 N.

Leave your answer in the comment section below I will help you solve it.