In the previous article, we discussed Pascal’s law which states the pressure or intensity of pressure at a point in a static fluid is equal in all directions. The Hydrostatic Law states that the increase of pressure in a vertically downward direction must be equal to the specific weight of the fluid at that point. Whereas, The Archimedes Principle states that the buoyant force on an object is equal to the weight of the fluid displaced by the object. Let us discuss the Hydrostatic law in more detail and prove it.

Hydrostatic law
Hydrostatic Law states that the rate of increase in pressure in a vertically downward direction must be equal to the specific weight of the fluid at that point.
The Hydrostatic Law obtains the pressure at any point in a fluid at rest.
Let us prove this Hydrostatic Law by finding the pressure variation in a fluid at rest…
Pressure Variation in a Fluid at Rest
Consider a small fluid element as shown in the following figure

Let us say
AA = Cross-sectional area of element
AZ = Height of fluid element
p = Pressure on face AB
Z = Distance of fluid element from the free surface.
The forces acting on the fluid element are
- Pressure forces on AB = p × A and acting perpendicular to face AB in the downward direction.
- Pressure force on CD,
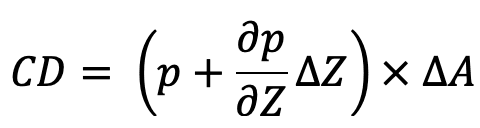
This pressure acts perpendicular to the face CD, vertically upward direction.
- Weight of fluid element = Density × g × Volume = p × g × (AA × AZ).
- Pressure forces on surfaces BC and AD are equal and opposite.
For equilibrium of fluid elements, we have
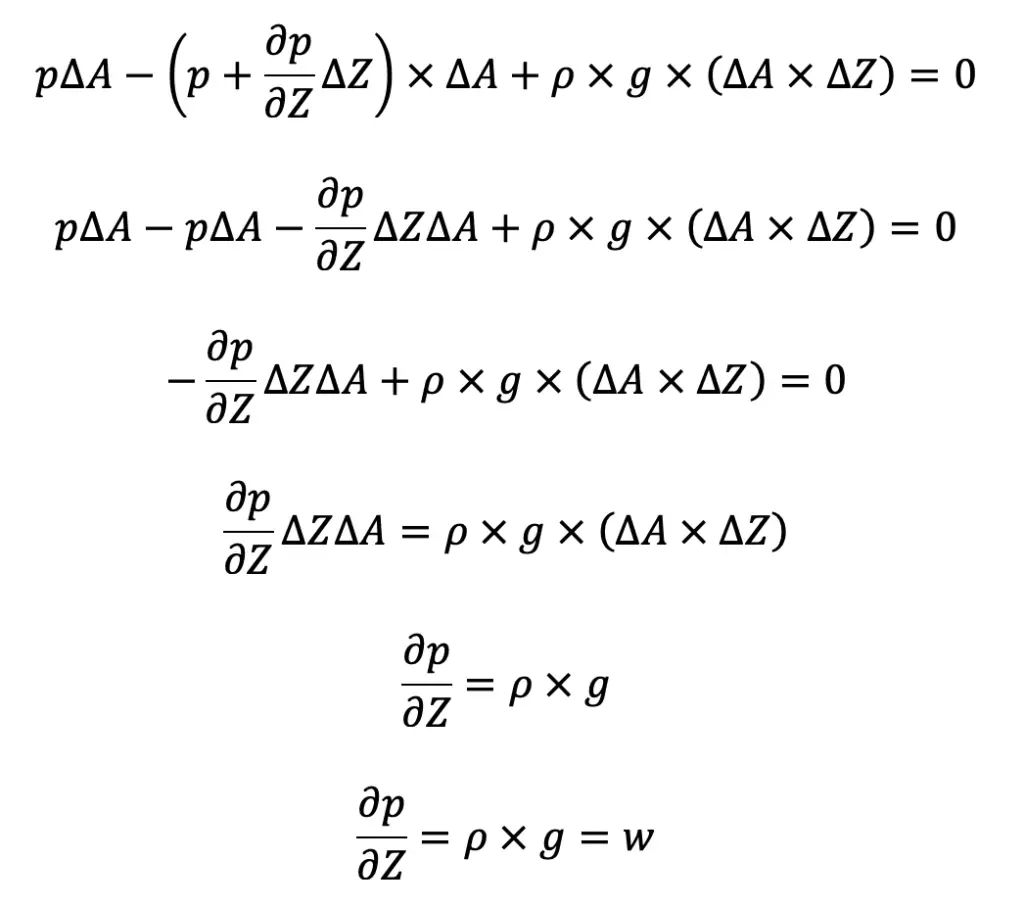
…….(∴ p × g = w)
where w = Weight density of the fluid.
The above equation (d) states that the rate of increase of pressure in a vertical direction is equal to the weight density of the fluid at that point. This is Hydrostatic Law.
By integrating the above equation for liquids, we get
∫dp = ∫ρgZ
or
p = ρgZ
where
p is the pressure above atmospheric pressure
Z is the height of the point from free surfaces.
From this equation, we also have to have
Z = p/ρg
Here Z is called Pressure Head.
Archimedes Principle
According to the Archimedes Principle, the buoyant force on an object is equal to the weight of the fluid displaced by the object.
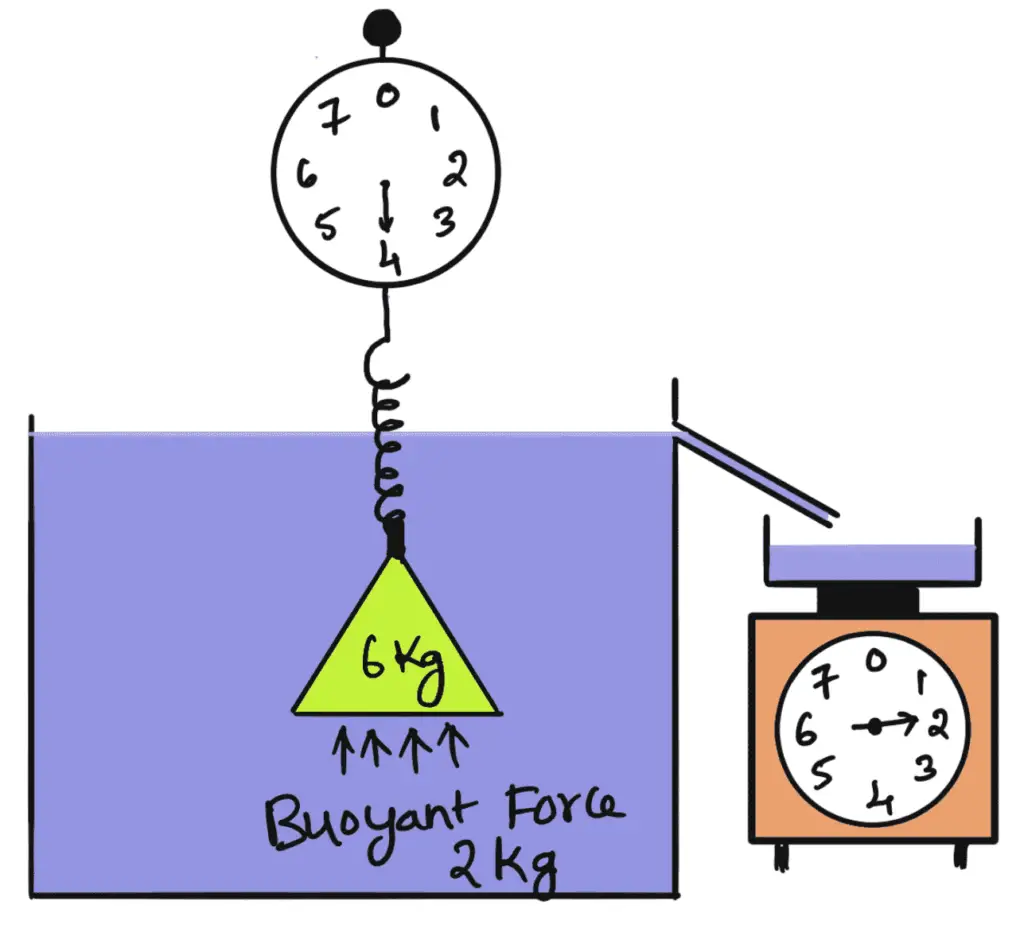
The Archimedes Principle states that “The upward buoyant force that is exerted on a body immersed in a fluid as shown above (whether partially or fully submerged), is equal to the weight of the fluid that the body displaces and acts in the upward direction at the centre of mass of the displaced fluid”.
What is Buoyant Force?
When a body is either wholly or partially immersed in a fluid, a lift is generated due to the net vertical component of hydrostatic pressure forces experienced by the body. This lift is called the buoyant force and the phenomenon is called buoyancy.
Similar to the above Hydrostatic law, we can derive the formula for the Archimedes Principle
We know the density formula ρ = Mass (m) / Volume (V)
From this, we can get the mass of the displaced liquid
Mass (M) = Density(ρ) × Volume (V)
The weight of the displaced liquid can be written as W = Mass (M) × Acceleration due to gravity (g)
W = M × g
W = ρ × V × g
As we stated that the apparent loss of weight is equal to the weight of the water displaced.
The Buoyant force are given by
Fb = ρ × V × g
Where
Fb is the Buoyant force
ρ is the density of the liquid,
V is the volume of liquid displaced
g is the acceleration due to gravity
Conclusion
We have briefly discussed the Hydrostatic law and the Archemedes Principle withe neat sketch. The difference between Hydrostatic Law and Archemedes Principle is that with Hydrostatic Law, we study the pressure variation at point in the fluid, where as the Archemedes Principle states about the object floating or immersed in the fluid. Let us know what do you think about this in the comment section below.

Leave a Reply