How to calculate Pressure of Atmosphere?

In the previous article, we have discussed the Gas constant in a very detailed manner, in which we have briefed about the Isothermal and Adiabatic Processes. In the Isothermal process, the temperature remains constant. Whereas the Adiabatic process, there is no heat exchange to and from the gas. Let us briefly discuss these to calculate pressure and the temperatures of the fluid under pressure. This is mostly used in Aeronautics, oceanography and metrology.

Pressure at a Point in Compressable Fluid

For compressible fluids, density (ρ) changes with the change in pressure and temperature. As we mentioned already these kinds of problems have huge scope in Aeronautics, oceanography and meteorology. Especially these problems help us when there is atmospheric air where density, pressure and temperature change with elevation.

Thus for fluids with variable density, the following Hydrostatic law equation discussed in the previous article cannot be integrated, unless the relationship between p and p is known.

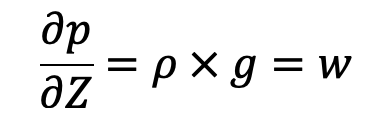
For gases the equation of state is

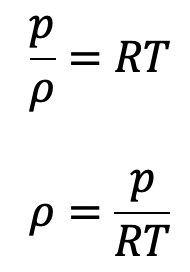
Now the above equation will be

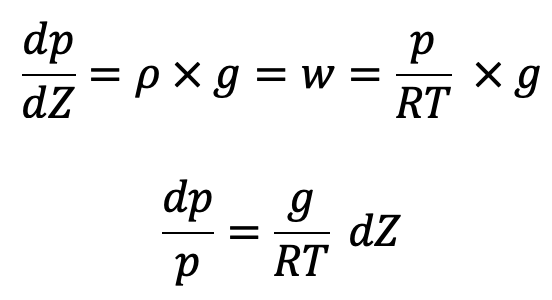
In the equation of Hydrostatic law, Z is measured vertically downward.

But if Z is measured vertically up, then

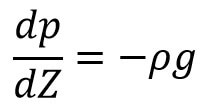
and hence the equation (b) will become

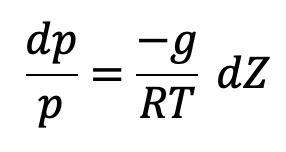
Isothermal Process

If temperature T is constant which is true for isothermal ess, equation (c) can be integrated as follows

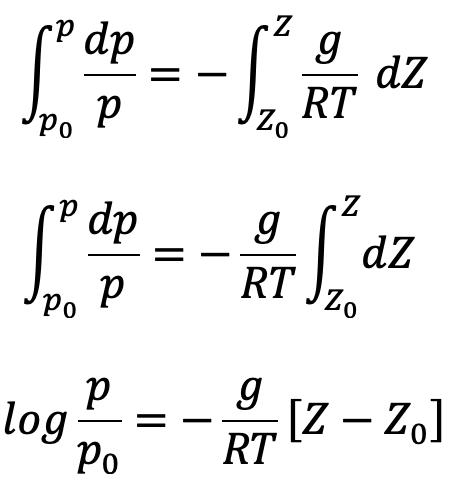
where p₀ is the pressure where height is Z₀. If the datum line is taken at Z₀, then Z₀ =0 and p₀ becomes the pressure at the datum line.

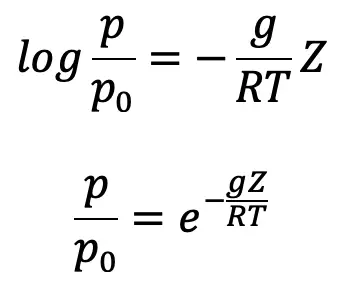
or pressure at a height Z is given by p = p₀ e^-gZ/RT …..(d)

Adiabatic Process

If temperature T is not constant but the process follows adiabatic law then the relation between pressure and density is given by

p/ρ^k Constant = C

where k is the ratio of constant.

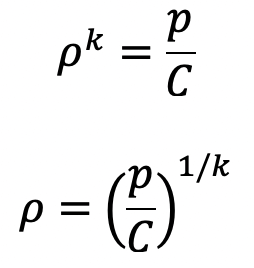
Then the equation of hydrostatic law for Z measured vertically up becomes,

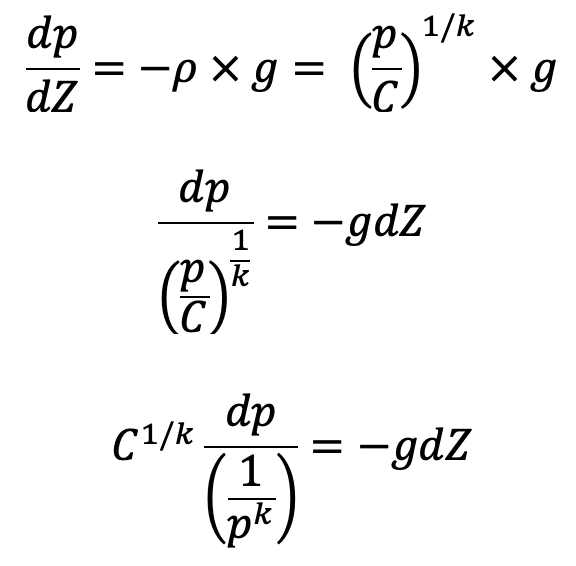
Integrating on both sides we get,

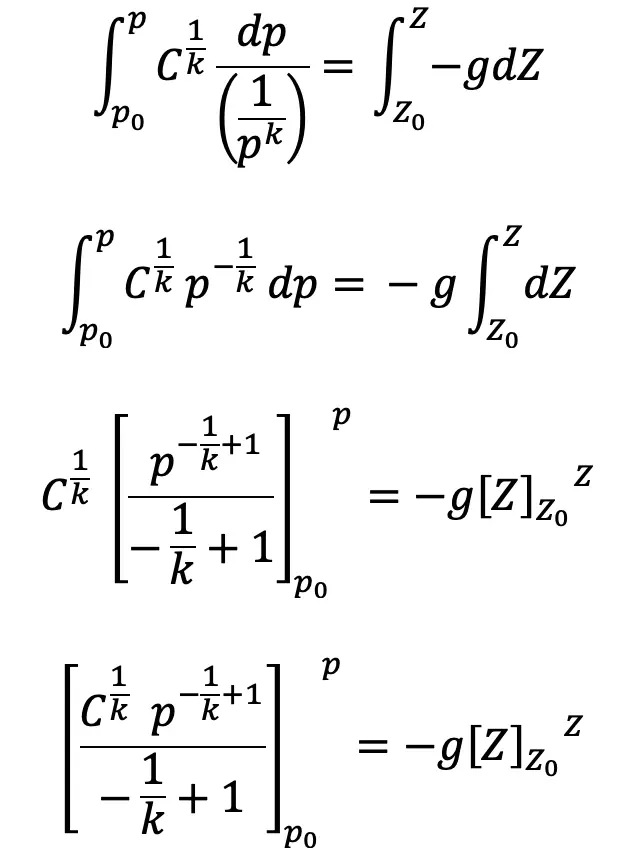
We have

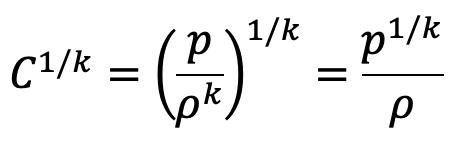
Substituting this value of C^1/k above we get

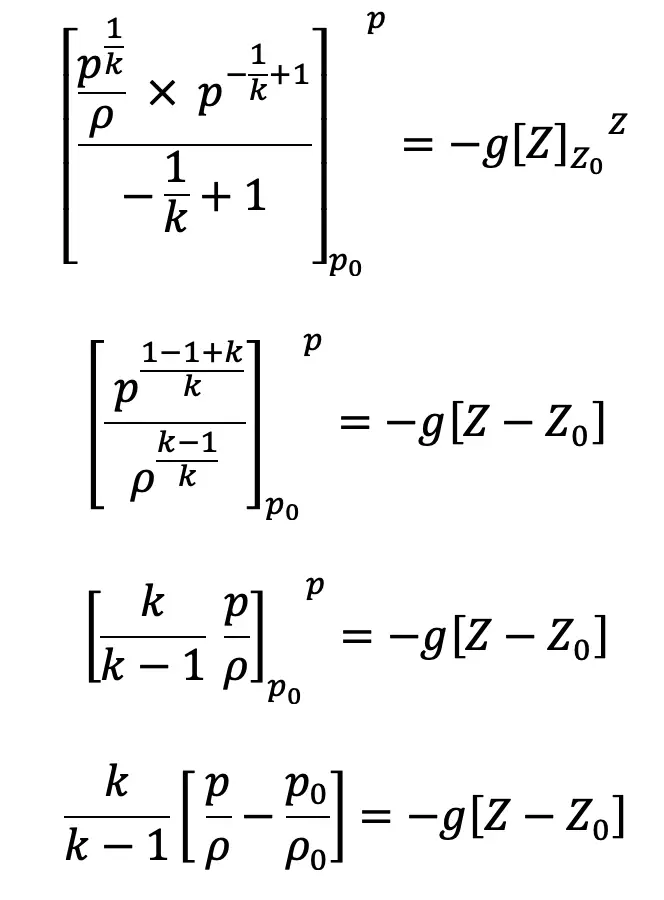
If the datum line is taken at Z₀, where pressure, temperature and density are p₀, T₀, ρ₀ then Z₀ = 0

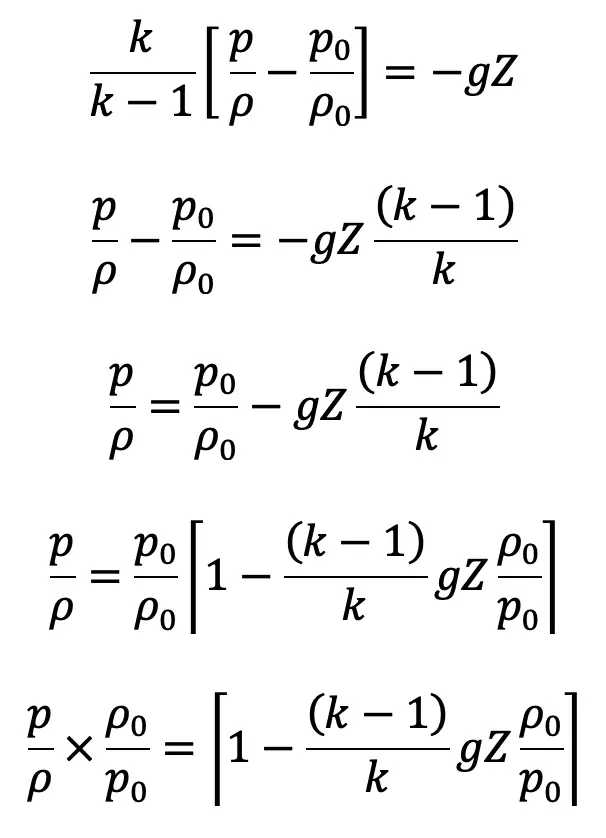
We know

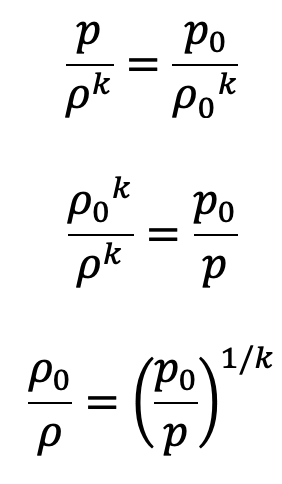
Substituting the value of ρ₀/ρ in the above equation, we get

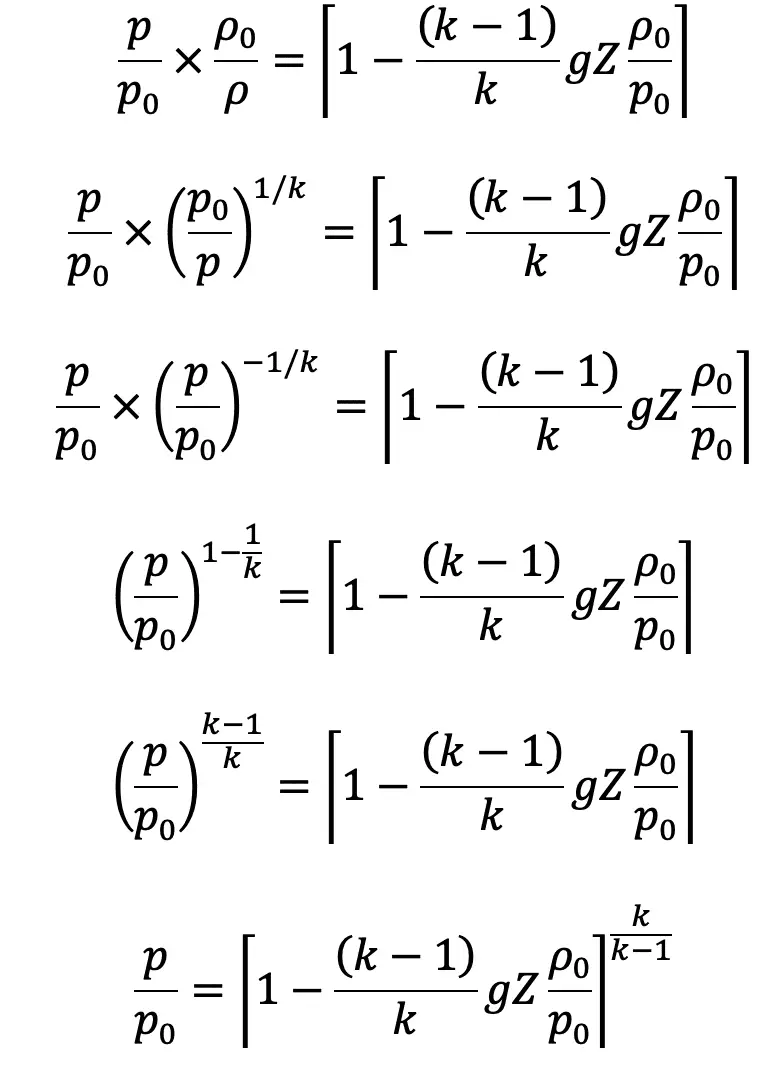
The pressure at height Z from the ground level is given by

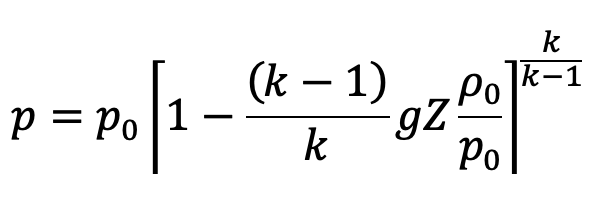
In the above equation (e)
p₀ = Pressure at ground level, where Z0 = 0
ρ₀ = Density of the air at ground level

The equation of state is

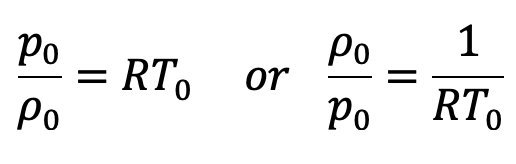
Substituting the values of ρ₀/p₀ in the above equation (e), we get

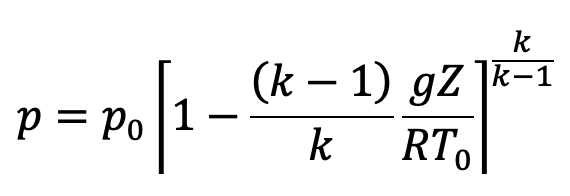
This is the equation to calculate the pressure at any point in the compressible fluid.

Temperature at any Point in Compressible Fluid

For the adiabatic process, the temperature at any height in the air is calculated similarly to the above derivation.

Equation Of State at ground level and at a height Z from ground level is written as

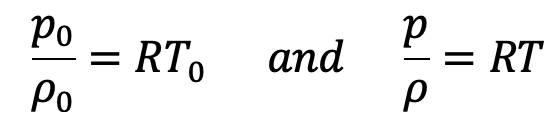
Dividing these equations we get

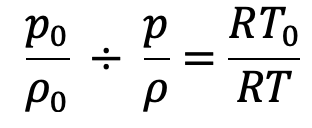
Further simplified and substituting the values we have from the above pressure equation (f), we get the following final derivation for the temperature.

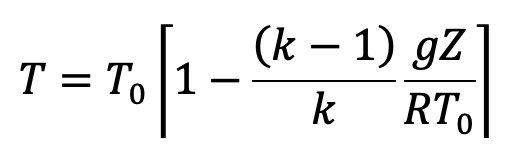
This is the equation to calculate the temperature at any point in the compressible fluid.

Temperature Lapse Rate (L)

It is defined as the rate at which the tem1Rrature changes with elevation. To obtain an expression for the temperature lapse rate, the temperature is given by equation (g) is differentiated with respect to Z as follows

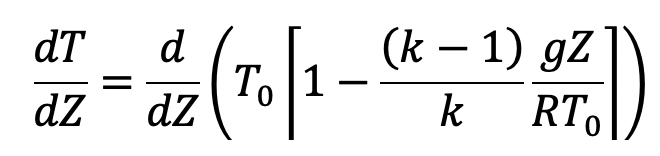
Where T0, K, g and R are constants.

The Temperature lapse Rate is denoted by L and hence

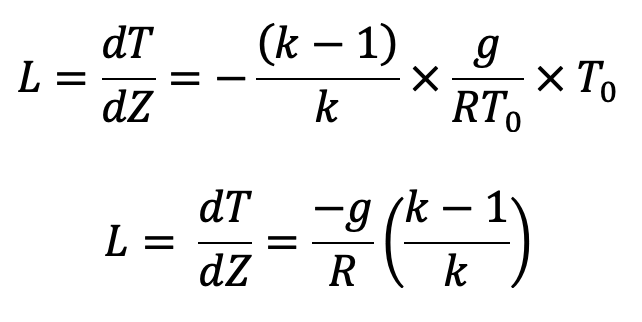
In the above equation (h),
(i) if k = I which means isothermal process, dT/dZ = 0, which means temperature dZ is constant with height.
(ii) If k > l, the lapse rate is negative which means temperature decreases with the increase in height.

In the atmosphere, the value of k varies with height hence the value of temperature lapse rate also varies.
From the sea level up to an elevation of about 11000m (or 11km), the temperature of the air decreases uniformly at the rate of 0.0065°C/m. from 11000m to 32000m, the temperature remains constant at -56.5°C and hence in this range lapse-rate is zero. The temperature rises again after 32000m m in the air.

Calculating Pressure on Sea Level

Let us solve an example problem to calculate the pressure of the atmosphere with different laws of fluids such as the isothermal adiabatic process.

Problem Statement: Calculate the pressure at a height of 7500 m above sea level if the atmospheric pressure is 10.143 N/cm² and the temperature is 15°C at sea level. assuming
(i) Air is incompressible.
(ii) Pressure variation follows isothermal law
(iii) Pressure variation follows adiabatic law
(Take the density of air the sea level is equal to 1.285 kg/m³. Neglect variation of g with altitude.)

Solution:

Height above sea-level Z = 7500m
pressure at sea-level p₀ = 10.143 N/cm² = 10.143 × 10⁴ N/m²
Temperature at sea-level t₀ = 15°C; T₀ = 273+15 = 288°K
Density of air, ρ = ρ₀ 1.285 kg/m³

(i) Pressure When air is incompressible

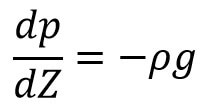
Intigrating the above relation on bothsides we get

p-p₀ = – ρg[Z-Z₀]
p = p₀– ρgZ
p = 10.143 × 10⁴– 1.258 × 9.81 × 7500
p = 101430-94543
p = 6887 N/m²

The pressure at a height of 7500 m above sea level if the atmospheric pressure is incompressible (p) = 0.6887 N/cm²

(ii) Pressure variation follows isothermal law

Using equation (d), we have

p = p₀ e^-gZ/RT

We have

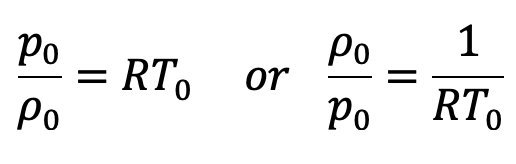
Substituting we get the following

p = p₀ e^-gZρ0/p0
p = 101430 × e ^{-7500×1.285×9.81/101430}
p = 101430 × e ^-0.9320
p = 101430 × 0.39376
p = 39939 N/m²

p = 3.993 N/cm²

The pressure at a height of 7500 m above sea level if the atmospheric pressure follows isothermal law is (p) = 3.993 N/cm²

(iii) Pressure variation follows adiabatic law

If the Pressure variation follows adiabatic law then k = 1.4

using the equation (e) we have

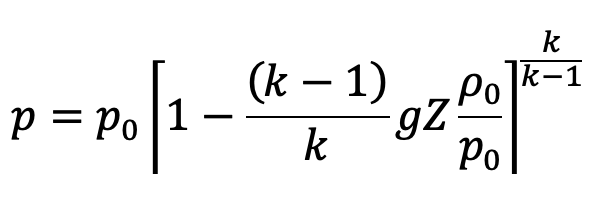
where ρ₀ = 1.285kg/m³

Substituting all the values we have, we will get

p = 101430 [1-0.2662]^3.5
p = 34310 N/m²

The pressure at a height of 7500 m above sea level if the atmospheric pressure follows adiabatic law is (p) = 3.431 N/cm²

This is how you can calculate the pressure on a sea level if you have the right inputs. Can you solve one more example problem on this topic…..?

Exercise Problem: If the atmospheric pressure at sea level is 10.143 N/cm2, determine the pressure at a height of 2500m assuming the pressure variation follows
(i) Pressure variation follows Hydrostatic Law
(ii) Pressure variation follows isothermal Law
(The density of air is given as 1.208 kg/m³)

Solve it and let me know the answers in the comment section below. All the best.