Find stiffness of the spring in Hartnell Governor

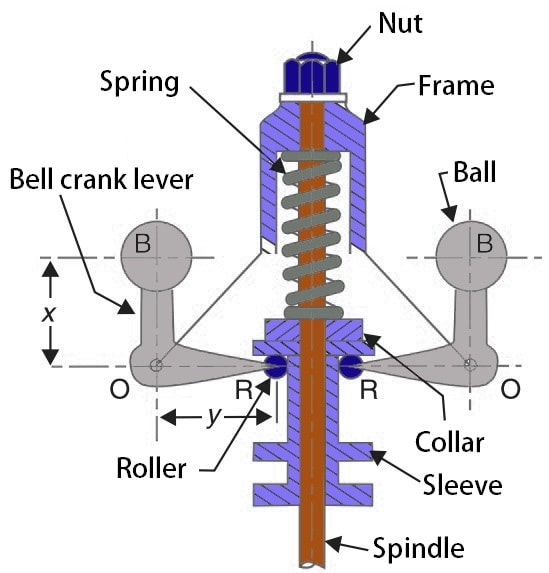
Hartnell Governor is basically a Centrifugal governor with a spring-loaded weight instead of dead weight on the sleeve to increase the speed of the balls required to lift the sleeve on the spindle. The Bell crank Lever holds two dead-weight balls for a Hartnell governor in order to regulate the fuel flow for the engines by maintaining the constant speed. Let us discuss how we can find the stiffness of the spring in Hartnell Governor. Also, design the Bell Crank Lever as well.

In the previous articles, we have different Mechanical Levers.

• Hand Lever (Hand Brake)
• Foot Lever (Brakes pedal, Foot pump Lever)
• Cranked Lever (Hoisting Winches)
• Lever Safety Valve
• Bell Crank Lever
• Rocker Arm for Exhaust Valve

In this article, we will discuss how we can determine the stiffness of the spring, the design of the bell crank lever, and the design of the balls for Hartnell Governor.

Bell Crank Lever

In a bell crank lever, the two arms of the lever are at right angles. Such types of levers are used in railway signaling, governors of Hartnell type, the drive for the air pump of condensers, etc. The bell crank lever is designed in a similar way as discussed in previous articles. The arms of the bell crank lever may be assumed of rectangular, elliptical, or I-section.

Stiffness of the Spring in Hartnell Governor

Let us discuss the complete design procedure for the bell crank lever with the following example.

In a Hartnell governor, the length of the ball arm is 190 mm, that of the sleeve arm is 140 mm, and the mass of each ball is 2.7 kg. The distance of the pivot of each bell crank lever from the axis of rotation is 170 mm and the speed when the ball arm is vertical is 300 rpm. The speed is to increase by 0.6 percent for a lift of 12 mm of the sleeve. We will find the necessary stiffness of the spring Design for the Hartnell Governor. Also, we will design the bell crank lever for the Hartnell Governor.

The permissible tensile stress for the material of the lever may be taken as 80 MPa and the allowable bearing pressure at the pins is 8 N/mm².

In order to find the stiffness of the spring, we will also design the bell crank lever and the dead weight of the balls.

Given design parameters of the Hartnell Governor are

Length of the ball arm x = 190mm
Length of the sleeve arm y = 140mm
Mass of each ball m = 2.7kg
Distance of the pivot of each bell crank lever from the axis of rotation  r₂ = 170mm =0.17m
Speed N₂ =300r.p.m.
Lift of sleeve h = 12mm
Permissible tensile stress σ_t = 80 MPa = 80 N/mm²
Allowable bearing pressure at pins p_b = 8 N/mm²

Stiffness of the Spring

Let
s₁ = Stiffness of the spring.

We know that the minimum angular speed of the ball arm (i.e. when the ball arm is vertical)

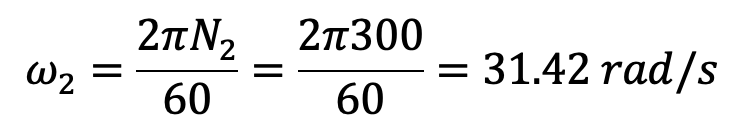
Since the increase in speed is 0.6 percent, therefore the maximum angular speed of the ball arm,

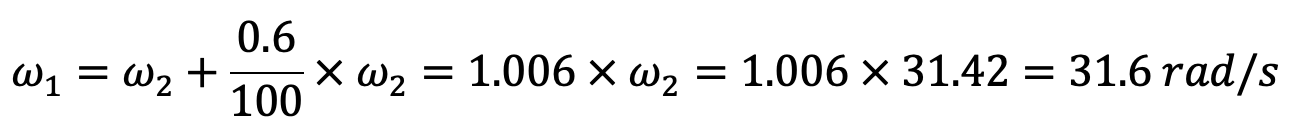
We know that the radius of rotation at the maximum speed,

r₁ = r₂ + h × x ÷ y = 170 + 12 × 190 = 186.3mm = 0.1863m

The minimum and maximum position of the ball arm and sleeve arm is shown in the following figures (left) and (right) respectively.

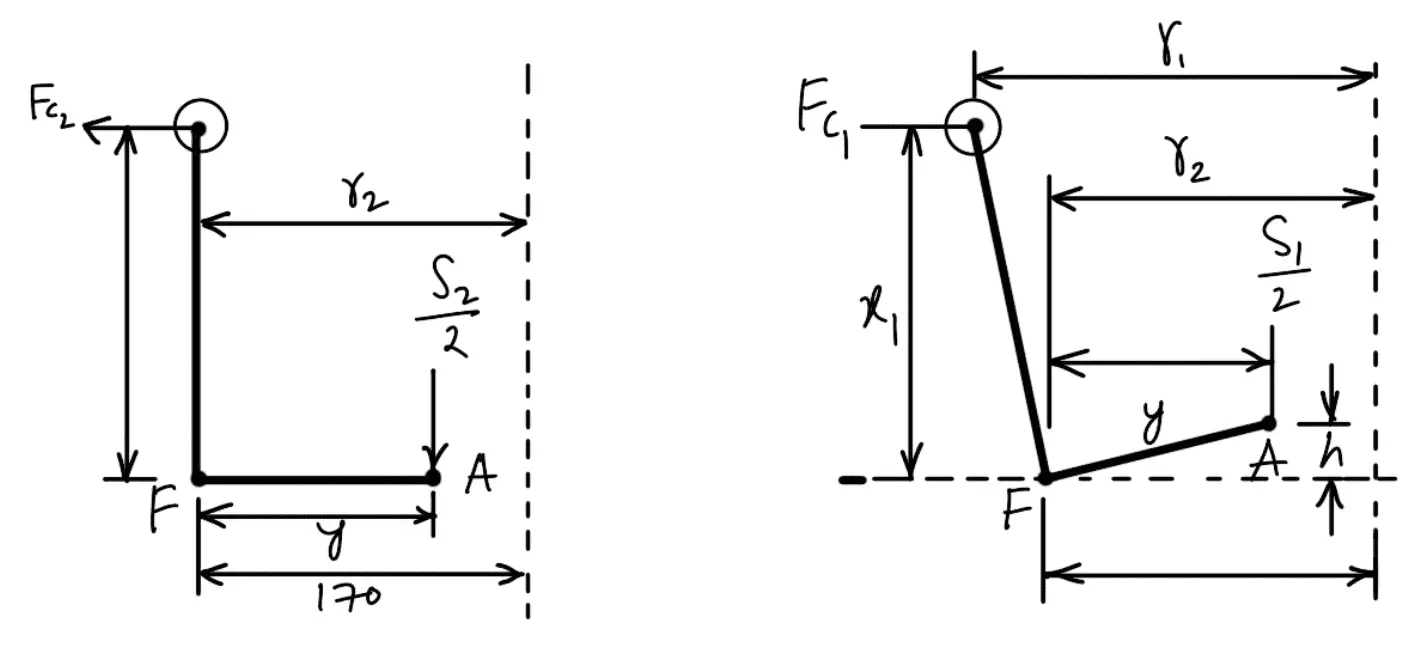
F_C1 = Centrifugal force at the maximum speed = m (ω₁)² r₁
F_C2 = Centrifugal force at the minimum speed = m (ω₂)² r₂
S1 = Spring force at the maximum speed (ω₁)
S2 = Spring force at the minimum speed (ω₂)

Taking moments about the fulcrum F of the bell crank lever, neglecting the obliquity effect of the arms (i.e. taking x₁ = x and y₁ = y) and the moment due to the mass of the balls, we have for the maximum position,

S₁ = 2F_C1 × x ÷ y
S₁ = 2m(ω₁)² × r₁ × x ÷ y
S₁ = 2 × 2.7 × (31.6)² × 0.1863 × 190 ÷ 140
S₁ = 1364N

Similarly

S₂ = 2F_C2 × x ÷ y
S₂ = 2m(ω₂)² × r₂ × x ÷ y
S₂ = 2 × 2.7 × (31.42)² × 0.17 × 190 ÷ 140
S₂ = 1230N

We already know that

S₁ – S₂ = h × s₁
s₁ = (S₁ – S₂) ÷ h
s₁ = (1364 – 1230) ÷ 12
s₁ = 11.16 N/mm

The Stiffness of the spring used for the Hartnell Governor is 11.16 N/mm.

Design of Bell Crank Lever

The bell crank lever is shown in the following figure. First of all, let us find the centrifugal force (or the effort P) required at the ball end to resist the load at A.

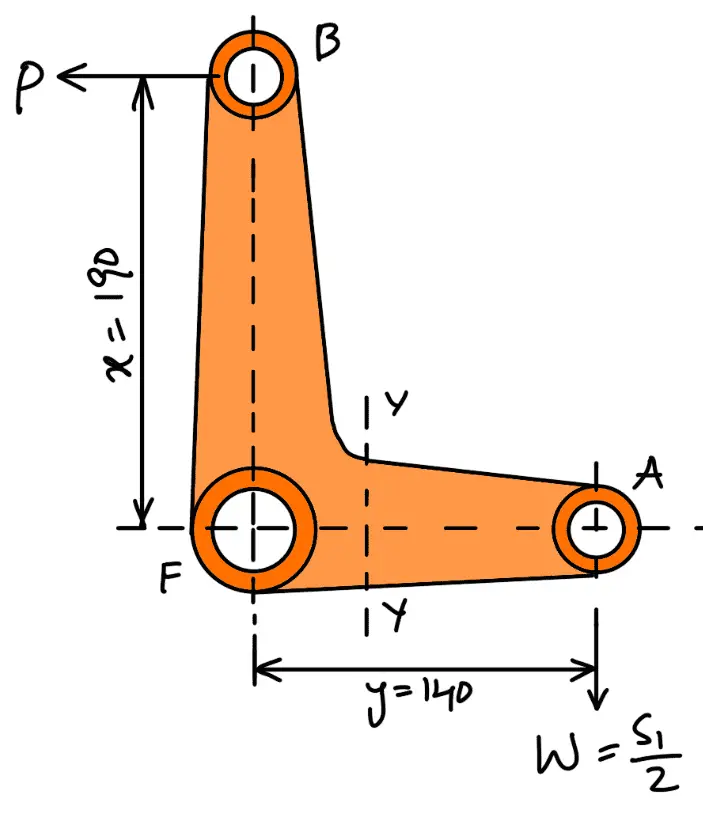
We know that the maximum load on the roller arm at A,

W = S₁ /2 = 1364/2 = 682N

Taking moments about F, we have

P × x = W × y

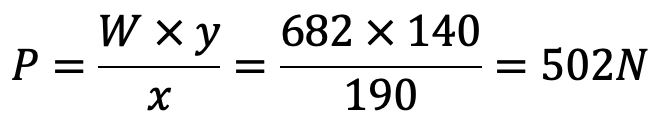
We know that reaction at the fulcrum F,

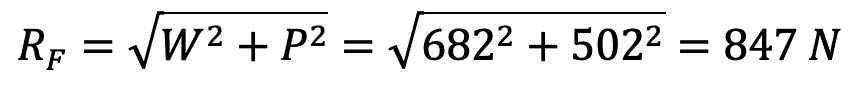
(a) Design For Fulcrum Pin

Let
d = Diameter of the fulcrum pin,
l = Length of the fulcrum pin = 1.25 d

The fulcrum pin is supported in the eye which is integral with the frame for the spring. Considering the fulcrum pin in the bearing. We know that load on the fulcrum pin (R_F),

847 = d × l × pb
847 = d × 1.25 d × 8
847 = 10 d²
d² = 847/10
d² = 84.7
d = 9.2

The diameter of the fulcrum pin is 10mm.

The length of the fulcrum pin t = 1.25 d = 1.25 × 10 = 12.5mm

Let us now check for the induced shear stress in the pin. Since the pin is in double shear, therefore load on the fulcrum pin (R_F),

847 = 2 × π × d² × τ
847 = 2 × π (10)² τ
847 = 157.1 τ
τ = 847 / 157.1
τ = 5.4 N/mm²
τ = 5.4 MPa

This induced shear stress is very much within safe limits.

A brass bush 3 mm thick may be pressed into the boss. Therefore diameter of the hole in the lever or the inner diameter of the boss = 10 + 2 × 3 = 16mm

and outer diameter of the boss = 2d = 2 × 10 = 20mm

b) Design for Lever

The cross-section of the lever is obtained by considering the lever in bending. It is assumed that the lever arm extends up to the center of the fulcrum from the point of application of load. This assumption results in a slightly stronger lever. Considering the weakest section of failure at Y-Y (40 mm from the center of the fulcrum).

∴ Maximum bending moment at Y-Y = 682 (140–40) = 68200N-mm

Let
t = Thickness of the lever,
B = Depth or width of the lever.

Section modulus,

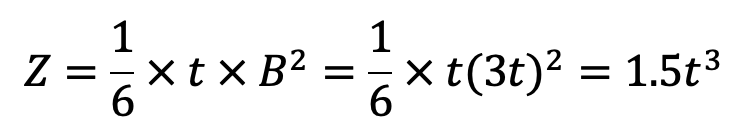
We know that bending stress (σ_b),

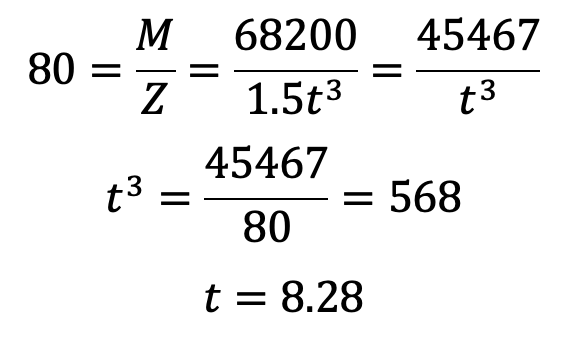
The thickness of the lever t is 10mm.

The depth or width of the lever is B = 3t = 3 × 10 = 30mm

Design for ball

Let r = Radius of the ball.

The balls are made of cast iron, whose density is 7200 kg/m³. We know that the mass of the ball (m),

2.7 = Volume × density
2.7 = 4 πr³ × 7200
2.7 = 30163 r³
r³ = 2.7 / 30163
r³ = 0.089/10³
r = 0.0447m
r = 44.7

The Radius of the ball r is 45mm.

The ball is screwed to the end of the lever. The screwed length of the lever will be equal to the radius of the ball.

The maximum bending moment on the screwed end of the lever,

M = P × r = 502 × 45 = 22590N-mm

d_c = Core diameter of the screwed length of the lever.

Section modulus,

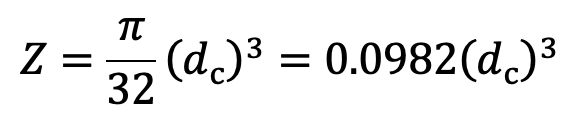
We know that bending stress (σ_b),

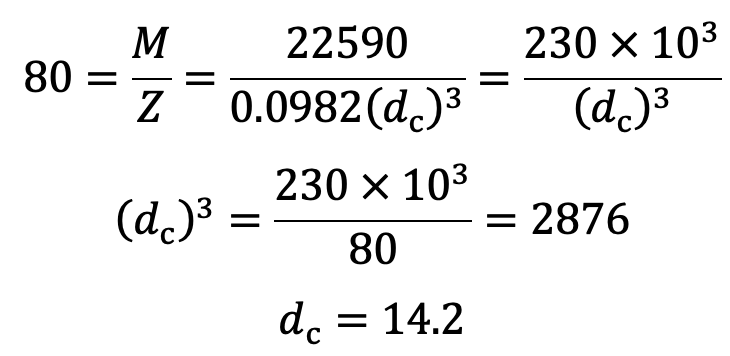
We shall take the nominal diameter of the screwed length of the lever as 16 mm.

Design for roller end A

Let
d₁ = Diameter of the pin at A,
l₁ = Length of the pin at A = 1.25 d₁

We know that the maximum load on the roller at A,

W = S₁ / 2 = 1364/2 = 682N

Considering the pin in the bearing. We know that load on the pin at A (W),

682 = d₁ × l₁ × p_b
682 = d₁ × 1.25d₁ × 8
682 = 10(d₁)²
(d₁)² = 682/10
(d₁)² = 68.2
d₁ = 8.26

The Diameter of the pin at A is 10mm

The Length of the pin at A is l₁ = 1.25 d₁ = 1.25 × 10 = 12.5mm

Let us now check the pin for induced shear stress. Since the pin is in double shear, therefore load on the pin at A (W),

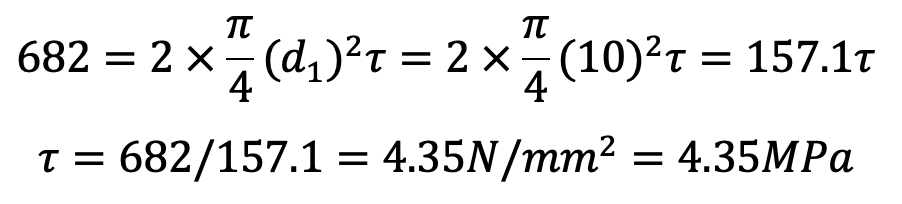
This induced stress is very much within safe limits.

The roller pin is fixed in the forked end of the bell crank lever and the roller moves freely on the pin.

Let us now check the pin for induced bending stress. We know that the maximum bending moment,

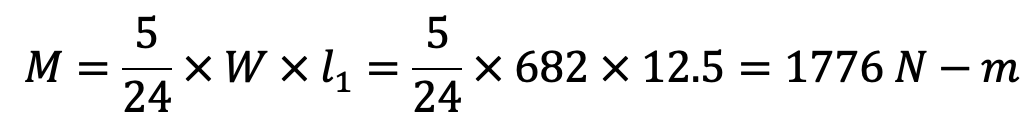
and section modulus of the pin,

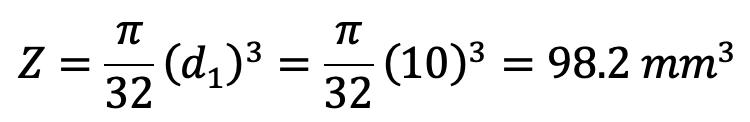
Bending stress induced

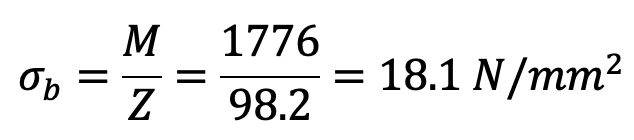
This induced bending stress is within safe limits.

We know that the thickness of each eye of the fork,

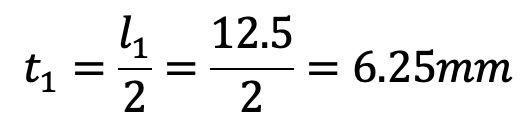
and outer diameter of the eye, D = 2 d₁ = 2 × 10 = 20mm

The outer diameter of the roller is taken slightly larger (at least 3 mm more) than the outer diameter of the eye. In the present case, the 23 mm outer diameter of the roller will be sufficient. The roller is not provided with a bush because, after sufficient service, the roller has to be replaced due to wear on the profile. A clearance of 1.5 mm is provided between the roller and fork on either side of the roller.

The total length of the pin,

l₂ = l₁ +2t₁ + 2 × 1.5 = 12.5 + 2 × 6.25 + 3 = 28mm

This is how you can determine the stiffness of the spring, the design of the bell crank lever, and the design of the balls for Hartnell Governor.