In a Machine, every component subjected to various forces. Due to these forces acting on the machine components, there are various types of stresses are induced. Where a simple stress is defined as the internal resistance force that opposes the external force per unit area. Where the Strain is defined as the deformation per unit length. Shear stress and shear strain are also defined in the same way. Let’s see How we can define them?

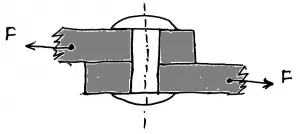When a body is subjected to two equal and opposite forces acting tangentially, across the resisting section, then the body tends to shear off the section. The stress induced in the section is known as the shear stress.

Make sense? Ok. let’s take an example to understand the scenario.

Shear Stress and Shear Strain

Let’s consider a Rivet is used to join two plates as shown in the figure. When two equal forces are acting on the two plates in opposite direction. Then a shear force is acted on the rivet and a shear stress will be induced at the cross-section of the rivet. If this load or force crosses the elastic limit then the rivet will fail as shown in the following fig.

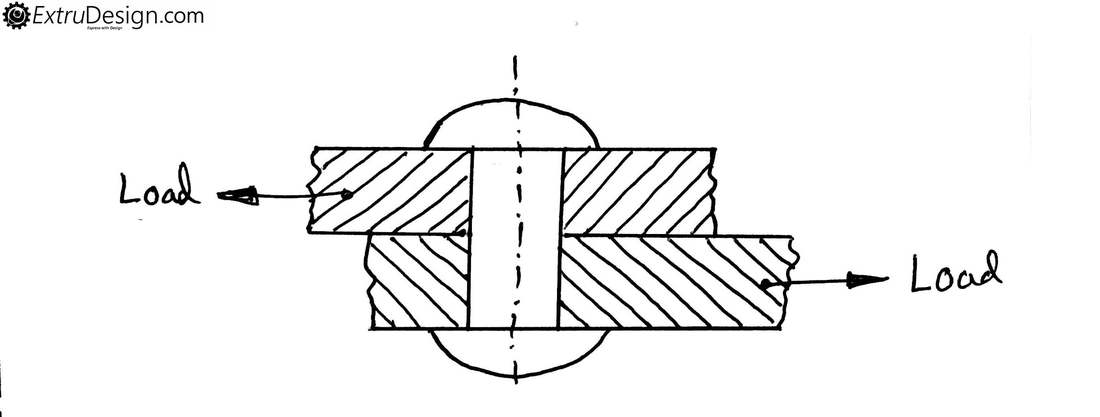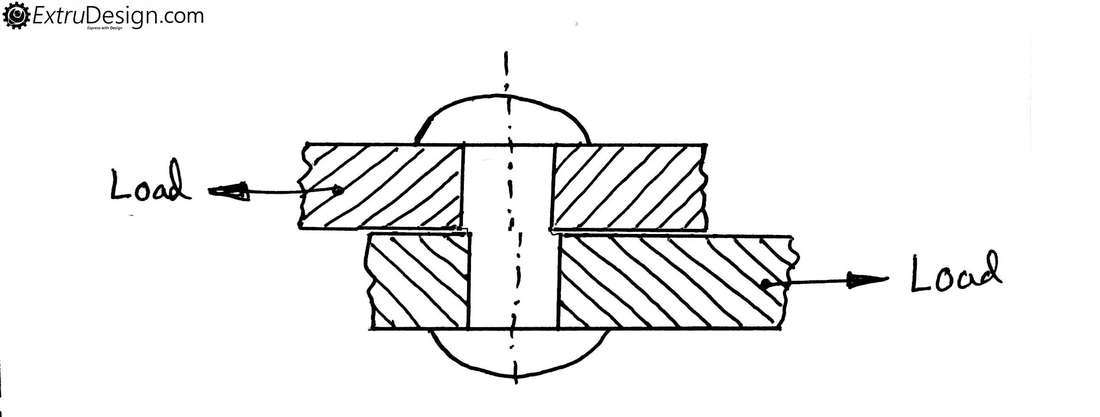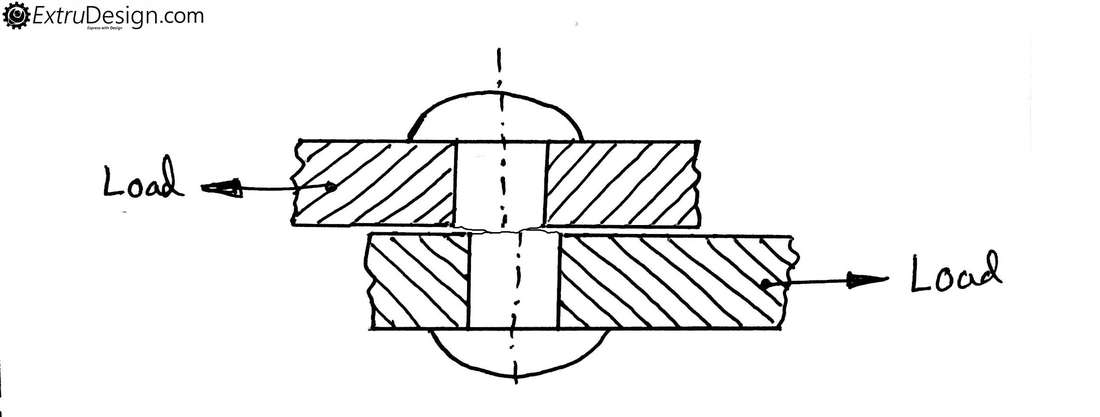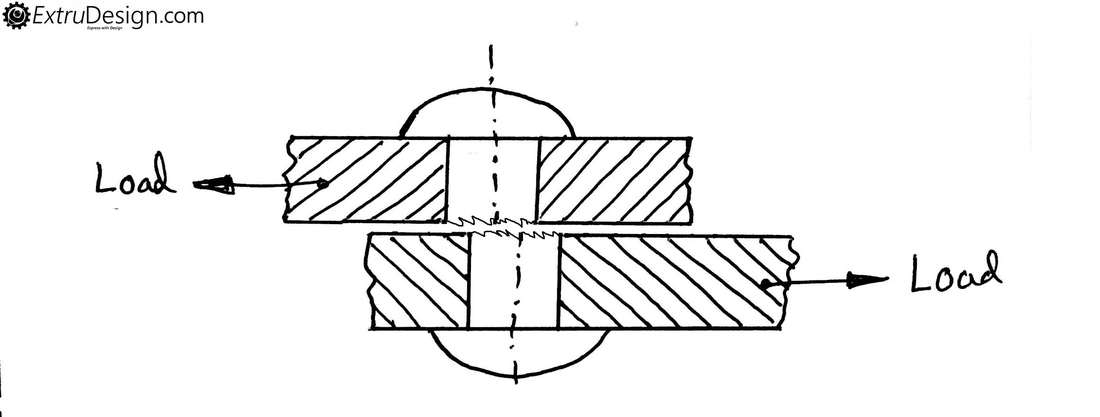
This Shear stress can be calculated as the ratio of Tangential force acting on the Rivet to the Crossection area of the Rivet.

Mathematically

Shear stress(τ) = Tangential Force/ Resisting cross-sectional Area.

Shear strain can be defined as the ratio of deformation to its original length or shape.

Shear strain can be represented by Φ

Here the shear stress directly proportional to the Shear strain within the elastic limit.

Shear Stress ∝ Shear Strain

τ ∝ Φ

τ = C * Φ

Where C= Constant of Proportionality Known the Modulus of rigidity or Shear Modulus.

Shear Modulus or Modulus of Rigidity

Shear modulus or  Modulus of Rigidity is by definition

“The ratio of the shear stress to the shear strain is known as shear modulus”

A material having a bigger shear modulus that means it will have high rigidity. So that’s why we call it as modulus of rigidity.

[Read the Full article about the Modulus of Rigidity Here]

Conclusion

The concept of shear stress and the shear strain are very useful in the design of fasteners. the Modulus of rigidity represents the how much strength is held by the fastener. It is a material property. Some of the commonly used materials are listed with the shear modulus.

Material	Modulus of Rigidity(C) in GPa (GN/m2) or (kN/mm2)
Steel	80 to 100
Wrought iron	80 to 90
Cast iron	40 to 50
Copper	30 to 50
Brass	30 to 50
Timber	10