When a machine component is subjected to a load (Static or dynamic load), it will experience the bending along its length due to the stress induced in it. This stress is known as Bending stress. Besides, there are other types of stress are also induced. They are Tensile stress, Compressive stress, Shearing stress, Bearing stress, Torsional stress. In this case, we supposed to consider the beam subjected to pure bending only to find out the bending stress in curved beams.

Bending stress

Bending stress is the normal stress induced in the beams due to the applied static load or dynamic load. The study of bending stress in beams will be different for the straight beams and curved beams. In this article, we will discuss the Bending stress in the curved beams.

Curved Beams

In the previous article, we have discussed the bending stress in straight beams (Initially straight). Now we are going to discuss the bending stress in curved beams (Initially curved).

• In Straight beam, it is considered that the centroidal axis and the neutral axis coincide. But in curved beams, it is considered that the neutral axis and the centroidal axis do not coincide rather the neutral axis will be shifted towards the centre of curvature.
• Due to the shifting of the neutral axis towards the centre of curvature, the stress distribution in the curved beam will be non-linear.

Wondered where we use the curved beams?

Have you seen the Crane hook?

Yes, crane hooks and chain links, Punches, presses and planers. these are the best examples for the initially curved beams.

Bending stress in Curved Beams

Consider an initially curved beam which is subjected to the bending moment M. The assumptions are made as same as the straight beams(Mentioned at the end of the article).  The following are the notable things that we will be observed while finding the bending stress in the curved beams.

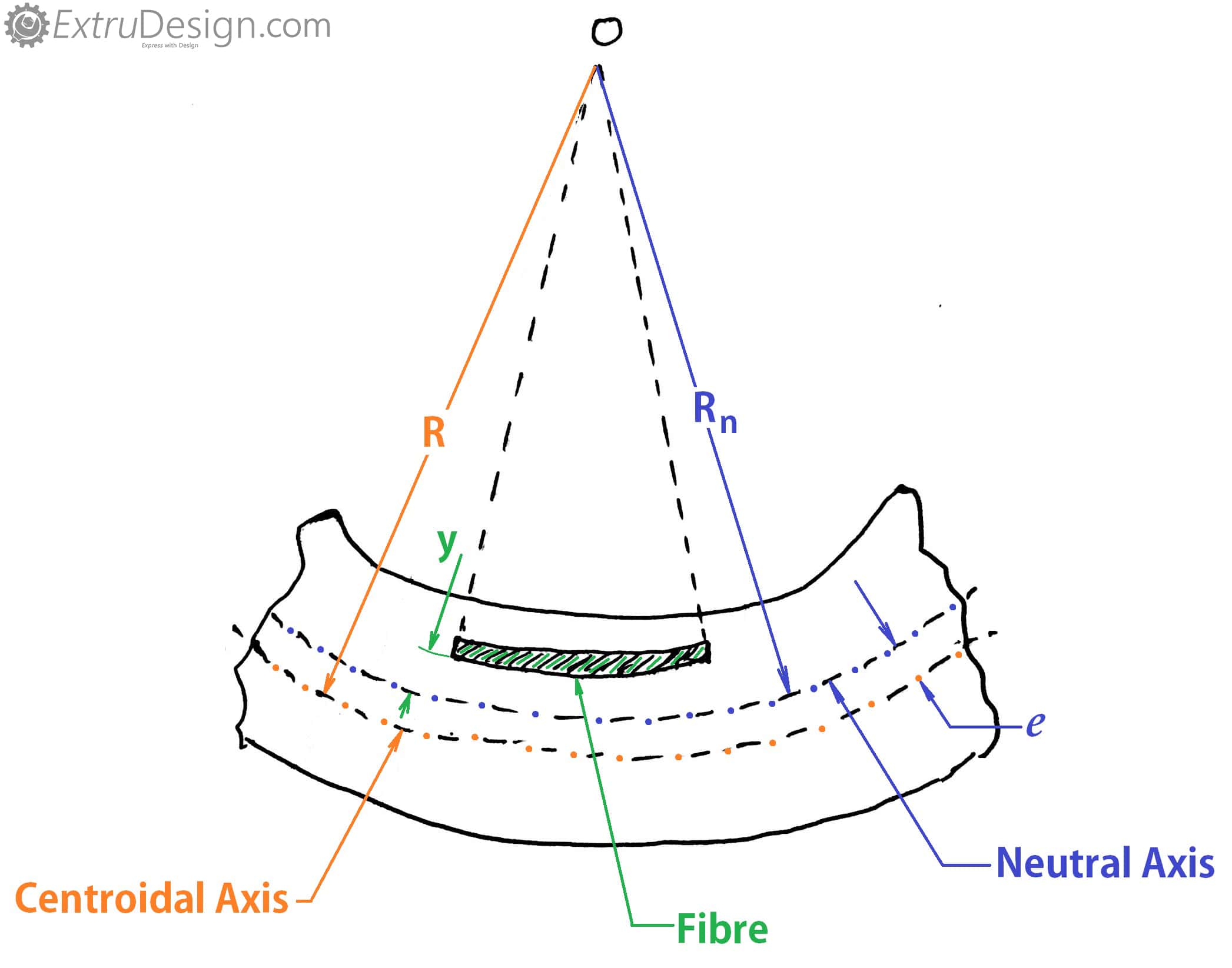
1. In curved beams, the bending stress induced in the inside fibres tends to tensile stress whereas the outside fibre tends to compress.
2. If the section is symmetric (Circular or the rectangle I-beam sections) the maximum bending stress will be induced in the inside fibre
3. If the section is unsymmetric then the maximum bending stress may be observed either in inside fibres or outside fibres. (See conclusion)

 

The bending stress at any fibre at a distance y from the neutral axis is given by

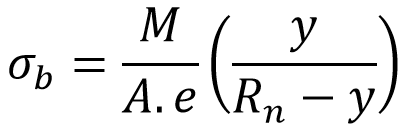
Where

M =Bending moment acting at the given section about the centroidal axis.

A = Area of cross-section

e = Distance from the centroidal axis to the neutral axis R – R_n

R = Radius of curvature of the centroidal axis

R_n = Radius of curvature of the neutral axis

y  = Distance between the neutral axis to the considered fibre which bending stress needed to be calculated

(+vefor distance towards the centre of curvature, -ve for the distance away from the centre of curvature)

from the above equation, we can find out the bending stress for the curved beam at any fibre.

Considerations in the Bending Stress in Curved Beams

There are some considerations has to made while finding the bending stress for the curved beams. They are as follows

• It has to consider that the material throughout the beam is same (Homogeneous material)
• It should obey the Hooke’s law (Stress is directly proportional to the strain in the beam)
• Each layer in the beam has to expand or contract freely and independently.
• The load should be applied in the plane(Plane of curvature) of bending
• The Young’s modulus is to be same for both the tension and the compression.

Conclusion

a) As we mentioned above If the section is unsymmetric then the maximum bending stress would be induced either at inside fibre or at outside fibre. By using these formulas we can calculate the bending stress

The maximum Bending stress at inside fibre is given by

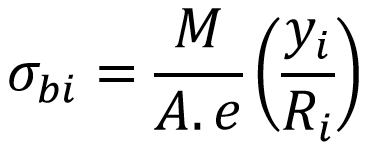
where

y_i  = Distance between neutral axis to the inside fibre = R_n-R_i

R_i = Radius of curvature of inside fibre

The maximum Bending stress at outside fibre is given by

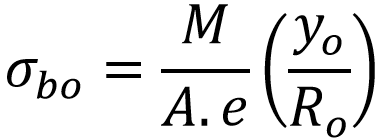
Y_o = Distance between neutral axis to the outside fibre = R_o – R_n

R_o = Radius of curvature of outside fibre

b) In addition to the bending moment if there is axial load then the axial load can be alphabetically added to the bending stress to obtain the resultant stress on the given curved beam.