What is Vortex Flow? | Equation of Motion of Vortex Flow

We have discussed the different types of fluid flows already, where we discussed 6 types to determine the velocity and the acceleration of the flow. Vortex Flow comes under laminar and Turbulent flow. Vortex flow is defined as the flow of a fluid along a curved path or the flow of a rotating mass. An example of this kind of flow is the Flow of liquid in the impeller, a whirlpool in a river. Let us discuss more details on the Vortex flow and the equation of motion of the vortex flow.

Vortex Flow

We have already mentioned that Vortex flow is defined as the flow of a fluid along a curved path or the flow of a rotating mass. Actually, there are two different types of Vortex flows.

1. Forced Vortex Flow
2. Free Vortex Flow

Let’s discuss these two types of Vortex flows in a Detailed manner.

Forced Vortex Flow

Forced vortex now is defined as that type of vortex flow, in which some external torque is required to rotate the fluid mass. The fluid mass in this flow, rotates at a constant angular velocity, ω.

The tangential velocity of any fluid particle is given by

v = ω × r

Where
r = Radius of the fluid particle from the axis of rotation

We all rewrite the above equation as follows,

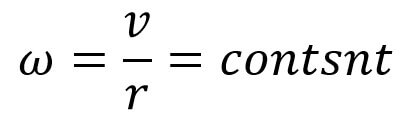
Some of the Forced Vortex flows are listed below.

• The juice mixer is the best example of Forced Vortex flow that we see daily as a household application
• Paint mixture as shown above is also one of the best examples of the forced Vortex Flow.
• The flow of fluid inside the impeller of a water pump is also the example
• The flow of water through the runner of the turbine.

Free Vortex Flow

When no external torque is required to rotate the fluid mass, that type of flow is called free vortex flow.

Thus the liquid in the case of the free vortex is rotating due to the rotation which is imparted to the fluid previously.

Examples of the free vortex flow are given below

• Flow of liquid through a hole provided at the bottom of a container.
• Flow of liquid around a circular bend in the pipe
• A whirlpool in a river.
• Flow of Fluid in a centrifugal pump casing.

The relation between velocity and radius, in the free vortex, can be obtained by putting the value of external torque equal to zero, or, the time rate of change of angular momentum. This means the Moment of momentum must be zero.

Consider a fluid particle of mass ‘m’ at a radial distance ‘r’ from the axis of rotation having a tangential v.

Then Angular momentum = Mass × m × v
Moment of momentum = Momentum × r = m × v × r

Time rate of change of angular momentum = ∂/∂t (m v r)

For free vortex ∂/∂t (mvr) = 0

Integrating om both sides we get

mvr = Constant
vr = Constant/m
vr = constant

…….Equation (b)

As you can see the application of the forced Vortex flow and the Free Vortex flow, have a huge role in the application of many applications ranging from the household to the industrial level. It is very important to study the flow and understand the equation of motion for these Forced and the Free Vortex flows.

Equation of Motion for Vortex Flow

Consider a fluid element ABCD (shown shaded) in the following figure.

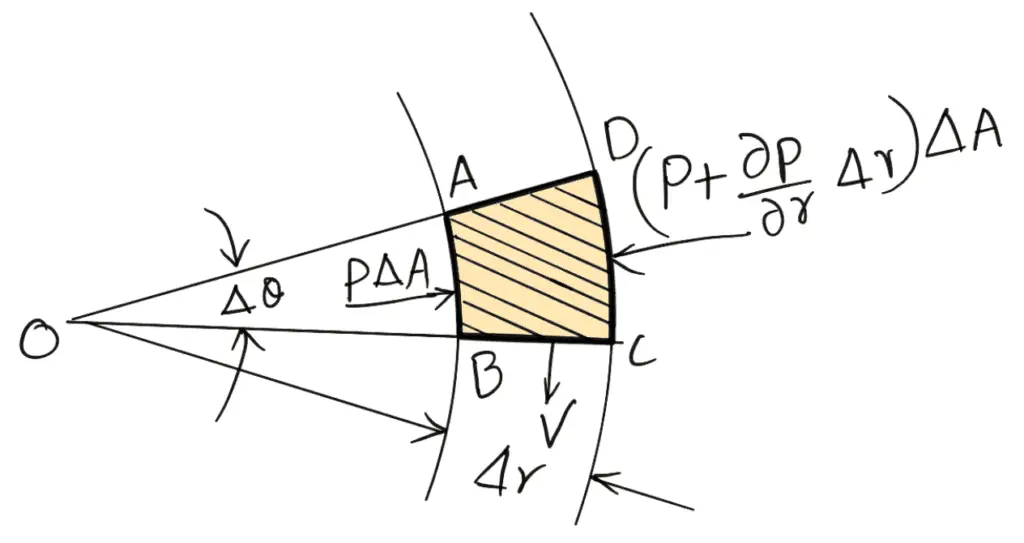
The fluid element is rotating at a uniform velocity in a horizontal plane about an axis perpendicular to the plane of the paper and passing through O.

Let us assume
r = Radius of the element from O.
Δθ = Angle subtended by the element at O.
Δr Radial thickness of the element.
ΔA = Area Of cross-section of Δ element.

The forces acting on the element are:

1. Pressure force, pΔA, on the face AB.
2. Pressure force, [p + (∂p/∂r) Δr] ΔA on the face CD.
3. Centrifugal force, mv²/r acting in the direction away from the centre O.

The mass of the element = Mass density × Volume

m = ρ × ΔA × Δr

Centrifugal Force = ρ × ΔA × Δr v²/r

Let us equate the forces in the radial direction,. we get the following

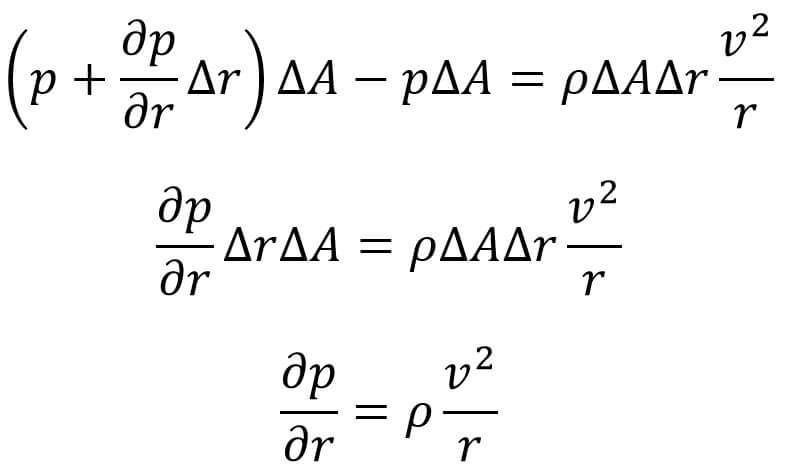
Equation (c) gives the pressure variation along the radial direction for a forced or free vortex flow in a horizontal plane.

The expression ∂p/∂r is called a pressure gradient in the radial direction.

As ∂p/∂r is positive, hence pressure increases with the increase of radius ‘r’.

The pressure variation in the vertical plane is given by the hydrostatic law as follows,

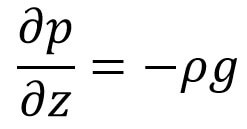
In the above equation(d), ‘z’ is measured vertically in an upward direction.

The pressure ‘p’ varies with respect to the ‘r’ and ‘z’ or ‘p’ is a function of ‘r’ and ‘z’. hence the total derivative of the ‘p’ becomes

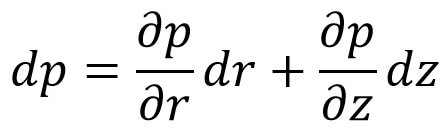
let us substitute the Equation (c) and the equation (d), and the above expression becomes as follows,

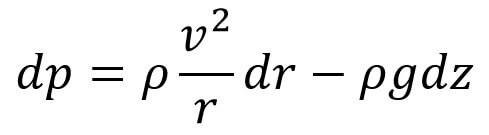
This equation (e) will give the variation of pressure rotating fluid in any plane. This is the equation of motion for the Vortex Flow.

Equation of Forced Vortex Flow

As we have already mentioned above that the tangential velocity of any fluid particle is given by

v = ω × r

Where
ω =Angular Velocity = Constant
r = Radius of the fluid particle from the axis of rotation

and we have the Equation of Motion for Vortex Flow from above

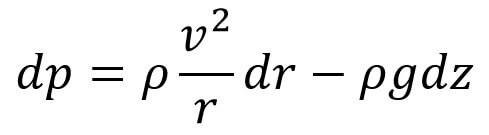
Let us substitute the value of v in this equation we get,

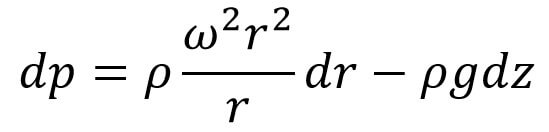
Let us consider two points(1 and 2) from the fluid as shown below figure where there is forced Vortex Flow.

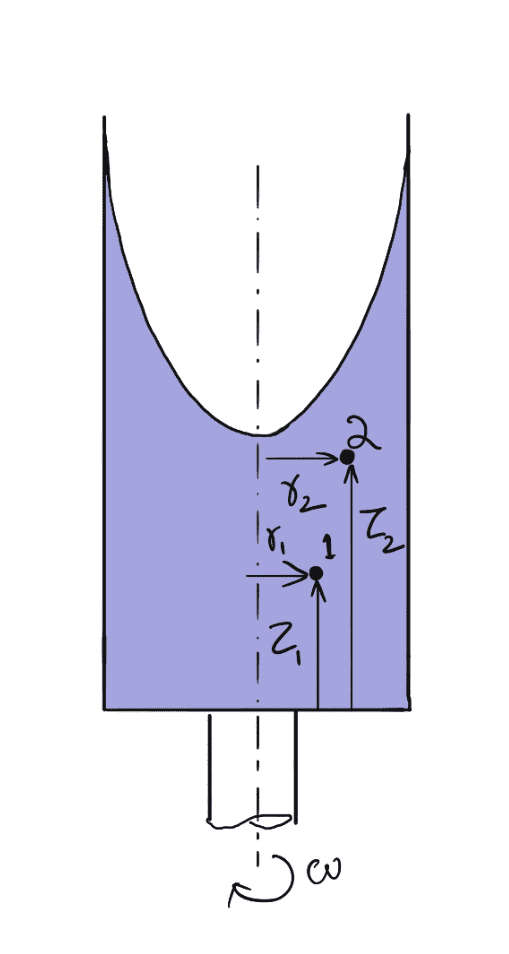
Integrating the Above equation for points 1 and 2 we get,

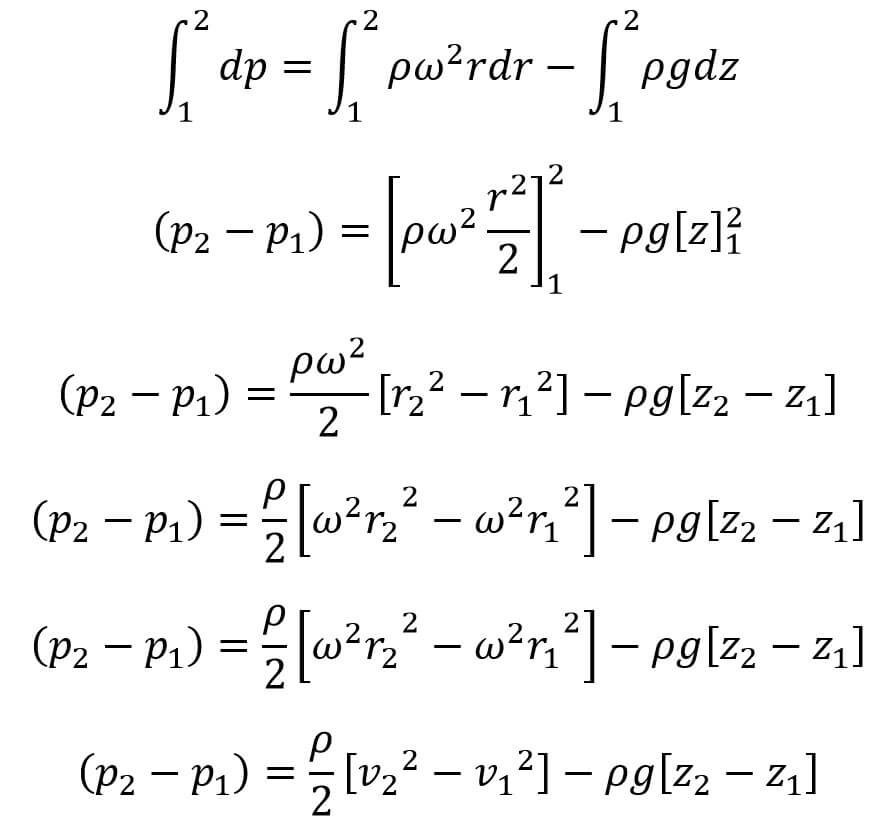
If these two points 1 and 2 are lying on the free surface of the fluid as shown in the following figure.

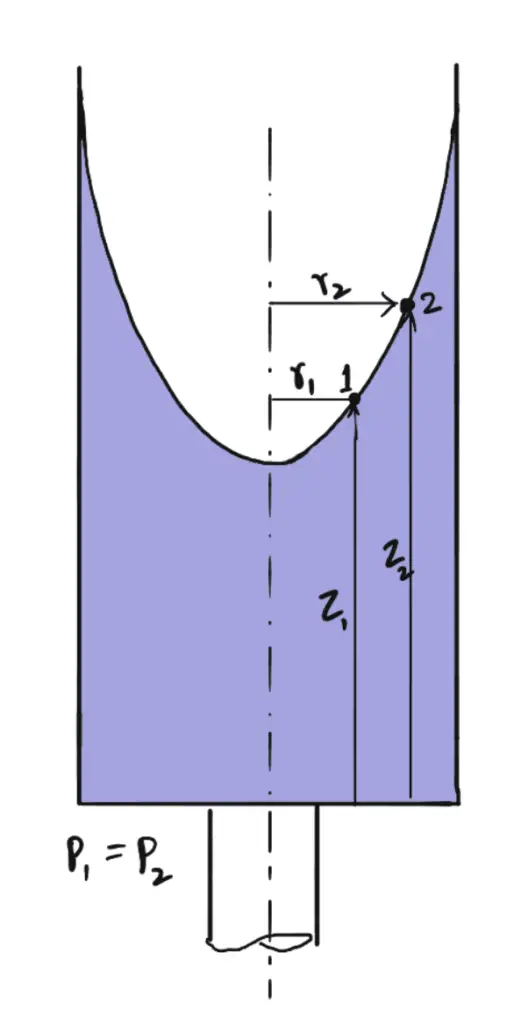
If the two points 1 and 2 are lying on the free surface then the p₁ = p₂ then the above equation becomes

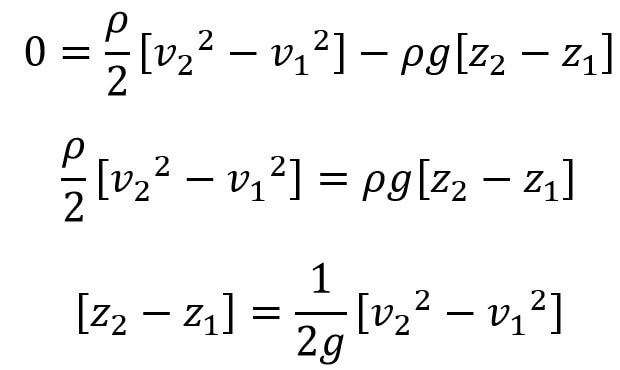
If the point 1 is lying on the axis of the rotation, then v₁ = ω × r₁ = ω × 0 = 0

the above equation can be written as follows

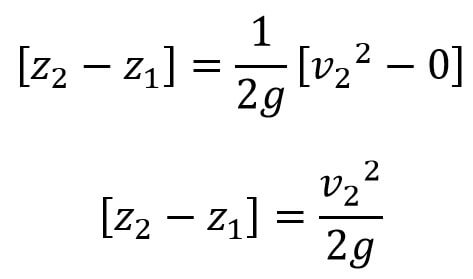
Let z₂ – z₁ = Z, then we can write the above equation

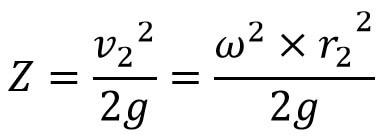
Thus Z varies with the square of r. Hence equation (f) is an equation of paraboloid.

This is all about the Equation of Motion for the Vortex Flow and the Forced Vortex Flow. Let us know what you think about this in the comment section below.