Velocity and Acceleration of a Fluid Flow

In the previous article, we discussed the types of Fluid flows, Fluid discharge (Q) and the Continuity Equations for a fluid flow. From the types of fluid flow, we can easily determine the velocity and acceleration components of the fluid flow.

Velocity

In fluid Mechanics, the velocity is defined as the change of position with respect to time or the displacement of the fluid in unit time. velocity is a vector quantity.

So the Velocity components are a function of space coordinates (i.e., length of direction of the flow) and time.

Now let us consider u, v, and w are the components in the x, y and z directions. and t is the time component.

Mathematically the velocity components can be written as follows,

u = f₁(x, y, z, t)
v = f₂(x, y, z, t)
w = f₃(x, y, z, t)

Let V is the resultant velocity at any point in a fluid flow, then we can write it as follows,

V = ui + vj + wk

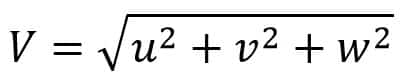
This is the resultant velocity at any point in a fluid flow.

Acceleration

In fluid Mechanics, Acceleration is defined as the rate of change of velocity of the fluid flow with respect to time. Acceleration is a vector quantity.

Let us assume a_x a_y and a_z are the total acceleration in x y and z directions respectively.

Then by the chain rule of differentiation, we can write

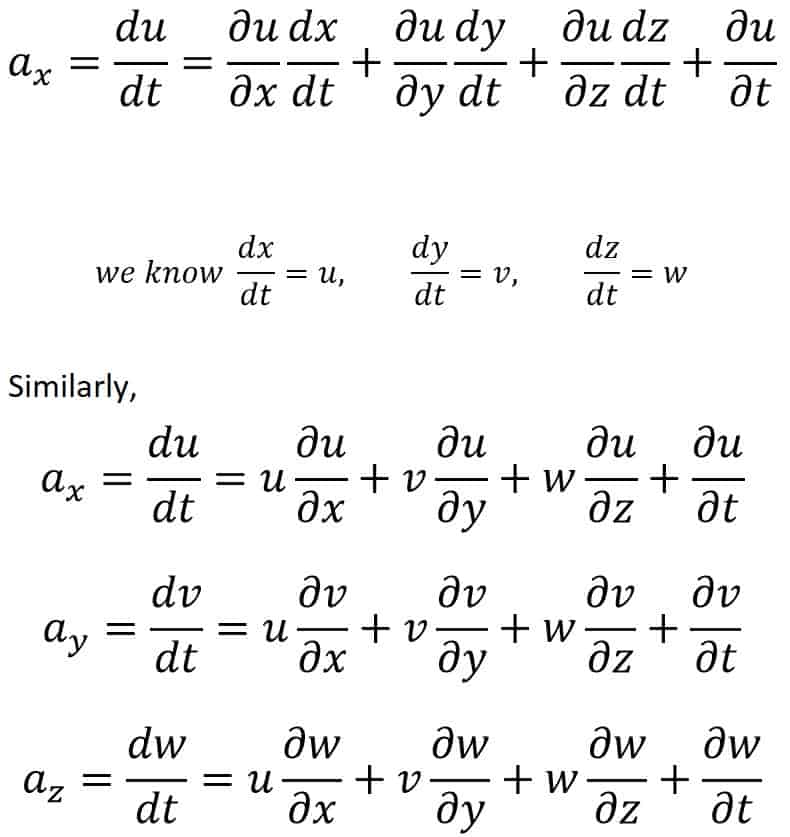
For steady flow, we know,

∂V/∂t = 0

where V is the resultant Velocity.

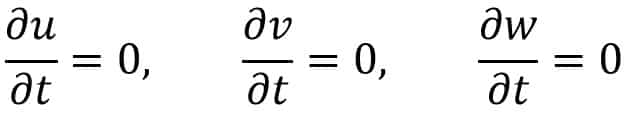
Hence the acceleration in the x, y and z directions can be written as

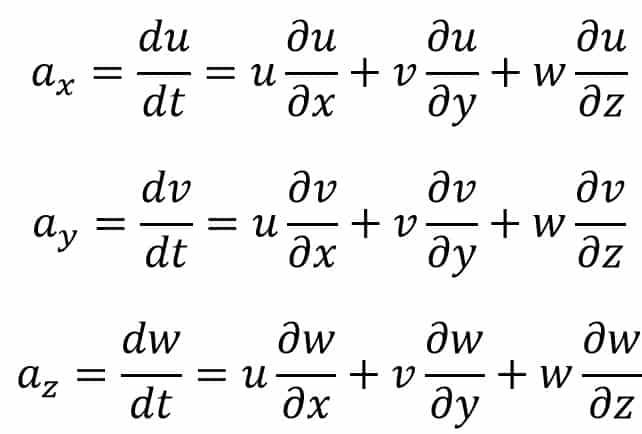
Equation (b)

The acceleration vector

A = a_xi + a_yj + a_zk

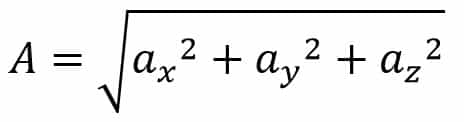
Local Acceleration and Convective Acceleration

Local acceleration is defined as the rate of increase of velocity with respect to time at a given point in a flow field.

In the equation given by (a), the following expression is known as local acceleration.

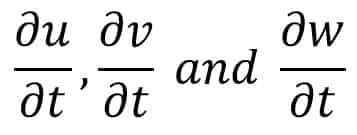
Convective acceleration is defined as the rate of change of velocity due to the change of position of fluid particles in a fluid flow.

The expressions Other than the following part in equation (a) are known as convective acceleration.

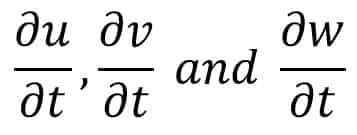
Example Problems to calculate Velocity and Acceleration of a Fluid Particle

Problem Statement: The velocity vector in a fluid flow is given as follows
V = (4x³) i – (10x²y) j + (2t) k
Find the velocity and acceleration of a fluid particle at (2, 1, 3) at time t = 1.

Answer:

Velocity

The velocity components u, v and w are
u = (4x³)
v = -(10x²y)
w = (2t)

from the point (2, 1, 3), we have x = 2, y = 1 and z=3 at time t = 1.

Hence velocity components (2, 1, 3) are

u = (4×2³) = 32 units
v = -(10×2²×1) = -40 units
w = (2×1) = 2 units

The velocity vector V at (2, 1, 3)

V = (32) i – (40) j + (2) k

The resultant Velocity will be

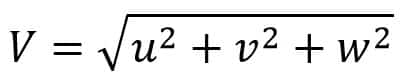
V = √[(32)² + (-40)² + (2)²]
V = √[1024+1600+4]
V = 51.26 units

Acceleration

The acceleration equation we know

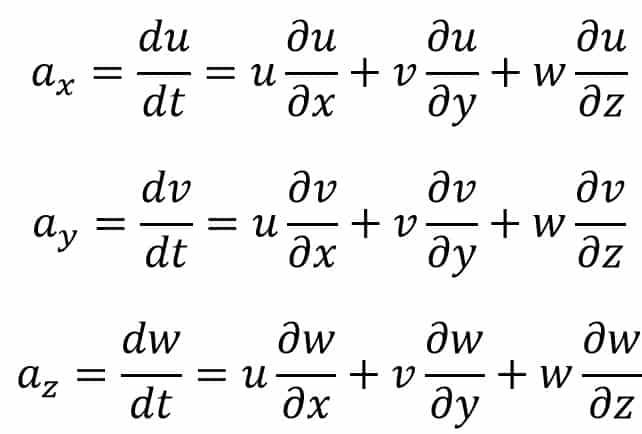
Now from velocity components we can write,

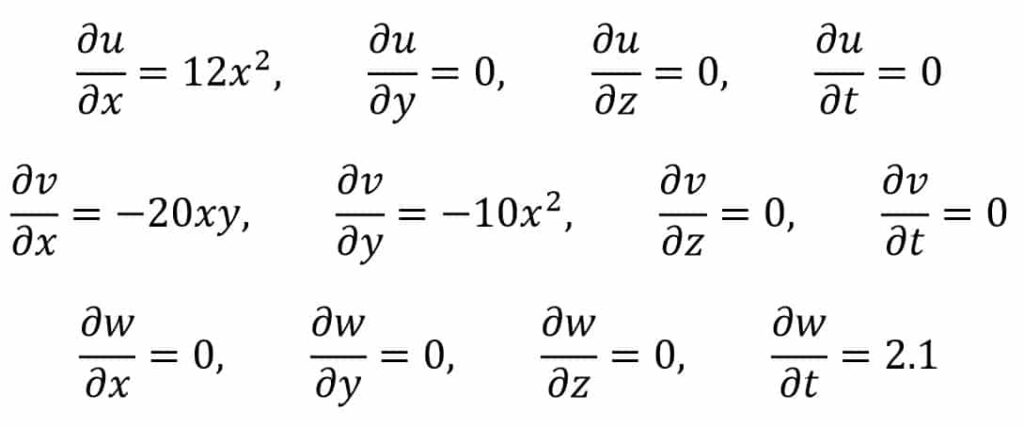
Substituting the values, the acceleration components at (2, 1, 3) at time t = 1 are

a_x = (4x³) × (12x²) + (-10x²y) × (0) + (2t) × (0) + 0
= 48x⁵
= 48(2)⁵
a_x = 1536 units

a_y = (4x³) × (-20xy) + (-10x²y) × (-10x²) + (2t) × (0) + 0
= -80x⁴y +100x⁴y
= -80(2)⁴(1) +100(2)⁴(1)
a_y = 320 units

a_z = (4x³) × (0) + (-10x²y) × (0) + (2t) × (0) + 2.1
a_z = 1536 units

The acceleration is A = a_xi + a_yj + a_zk

A = 1536i +320j + 2k

The resultant acceleration is

A = √[(1536)² + (320)² + (2)²]
A = √[2359296+102400+4]
A = 1569 units

This is how you can calculate the Velocity and Acceleration of any Fluid Particle from the given velocity vector equation.

Let us know what you think about this article in the comment section below.