An Engine is a device which transforms one form of energy into another form of Energy. An internal combustion engine is a heat engine where it undergoes different cycles of operations in a sequent manner to convert the thermal energy into useful work. In this article, we are going to discuss the 4 Stroke Diesel Engine working principle. 4 Stroke Diesel Engine is also known as the 4 stroke Compression Ignition Engine.

Working Principle of Engines

IC engines work on either Spark ignition or the Compression Ignition working principle.

Spark Ignition: Usually a petrol engine, where the combustion process of the air-fuel mixture is ignited by a spark from a spark plug

compression ignition: Generally the Diesel Engines, where the combustion process is caused by the elevated temperature of the air in the cylinder due to the mechanical compression.

4 Stroke Diesel Engine | 4 Stroke Compression Ignition Engine

• The 4 stroke Diesel engine is similar to the 4 Stroke Petrol Engine but the only difference is that in 4 Stroke Petrol engine we use the Sparkplug to ignite the air-fuel mixture, In Diesel engines (Compression Ignition Engines), we use high compression ratio to air to reach high temperature which is sufficient to self-ignite the injected the fuel.
• The compression ratio of the Diesel engines is ranging from 16 to 12 where the Petrol engines it will be around 6 to 10.
• In 4 Stroke Diesel Engine, the Thermodynamic cycle will be completed in the four strokes of the position or the two revolutions of the crankshaft.
• All the four strokes will be completed in the 720° of the crank rotation.
• During these four-strokes, there are five actions/events to be completed. they are suction and the compression combustion, expansion, exhaust.
• This 4 Stroke Diesel Engine was invented by Rudolf Diesel in 1876, so this why this Engine is called the Diesel Engine.

The cycle of operation of a four-stroke Diesel engine consists of the following strokes: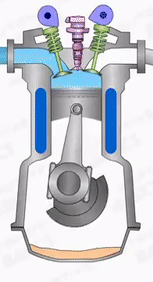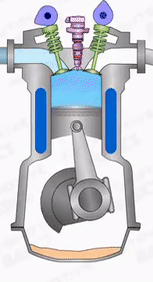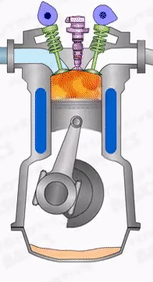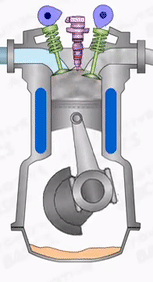

1. Suction or intake stroke,
2. Compression stroke,
3. Expansion or power stroke,
4. Exhaust stroke.

Suction or intake stroke

Suction Stroke starts when the piston is at the top dead centre(TDC) and about to move downwards. At this time the Inlet valve is opened and the exhaust valves are closed.

Suction will be created in the cylinder due to the movement of the piston downwards (Bottom Dead centre) the air will be drawn into the cylinder.

When the piston reaches the bottom dead centre (BDC), the suction stroke will end.

Compression stroke

Compression Stroke starts right after the suction stroke completes. i.e the piston reaches the BDC.

During the Compression stroke, the piston moves from the Bottom Dead Centre(BDC) to the Top Dead Centre (TDC). Due to this, the air which is drawn into the cylinder will be compressed. During this stroke, both the inlet and exhaust valves are closed.

The air which is occupied by the cylinder is compressed into the clearance volume which is available when the piston is at the TDC. This volume is called clearance volume.

Now the fuel is injected into the cylinder by the high-pressure fuel injecter at the end of compression stroke. Due to the high compression of the air in the cylinder, the pressure and temperature of the air are increased which is sufficient to self-ignite the fuel which is injected at the end of the compression Stroke.

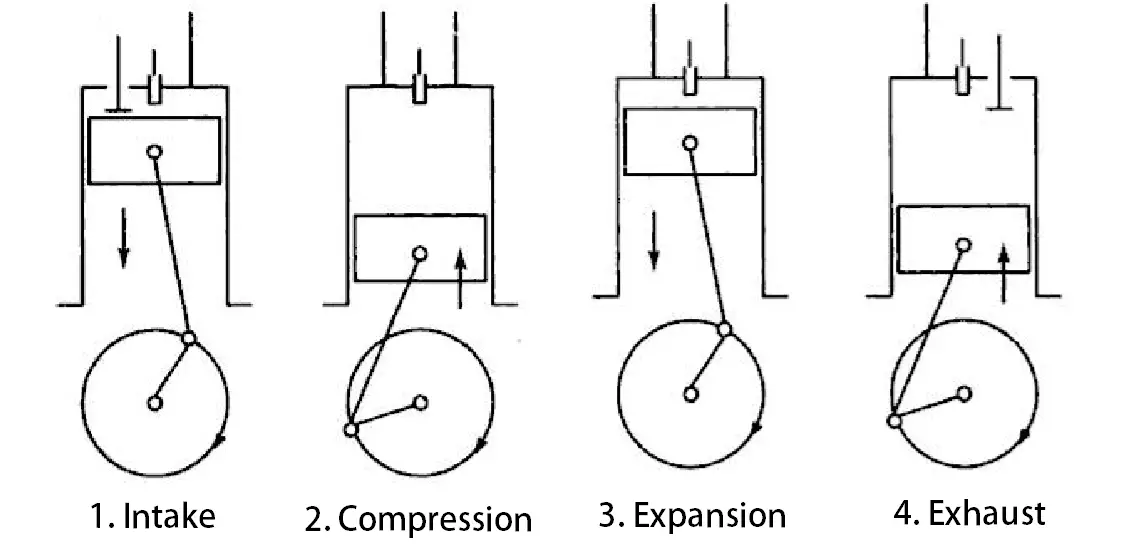
These two strokes (i.e., suction and compression stroke) complete one revolution of the crankshaft. i.e. 360° of crankshaft rotation.

Expansion or power stroke

During expansion stroke, both the inlet and exhaust valves remain closed.  The high pressure of the products of combustion pushes piston from Top Dead Centre (TDC) to Bottom Dead Centre(BDC).

It is also called as working stroke as the linear movement of the piston is converted into the rotational movement by the cranks shaft.

There is a flywheel is mounted on this crankshaft to collect the excess amount of the energy during the power stroke and helps the remaining three ideal strokes.

Exhaust stroke

At the end of the expansion stroke, the exhaust valves are open to exhaust the burnt gases out of the cylinder.

During the exhaust stroke, the inlet valves will remain closed.

In this stroke, the piston starts moving from the Bottom Dead Centre(TDC) to the Top Dead Centre(TDC) and sweeps all the burnt gases from the cylinder into the atmosphere. With this, the exhaust process will be completed.

These two strokes (i.e., expansion and exhaust strokes) complete one revolution of the crankshaft. i.e. 360° of crankshaft rotation.

now the cycle repeats from the first step again as the intake.

Conclusion

The working principles of the internal combustion engines are the Spark ignition and the compression ignition. The 4 stroke engine is available in both the Spark ignition and the compression ignition. We have discussed the 4 stroke engine with the Compression ignition engine, i.e. Diesel Engine. also, read the 4 Stroke Spark ignition engine. If you have any thoughts, leave them in the comments section below.