How to Design a Piston Rod?

Among the basic components of an Internal Combustion engine, the Piston rod is one of the most critical components. Since this Piston rod moves forward and backward in the engine cylinder, it is subjected to alternate tensile and compressive forces. It is usually made of mild steel. One end of the piston rod is secured to the piston by means of a tapered rod provided with a nut. The other end of the piston rod is joined to the crosshead by means of a cotter. Let us see how we can Design a Piston Rod for an internal Combustion engine.

Let us assume the piston rod experiences the column action and is being loaded eccentrically for every expansion stroke.

We can consider the previously derived equation to determine the maximum intensity of compressive stress when Long Columns are subjected to Eccentric Loading.

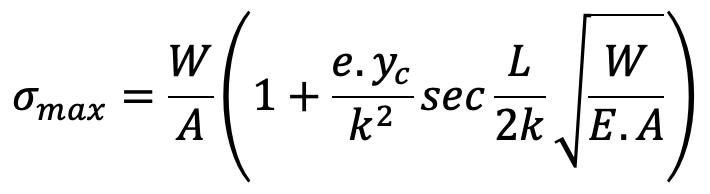
We can rewrite this expression as follows

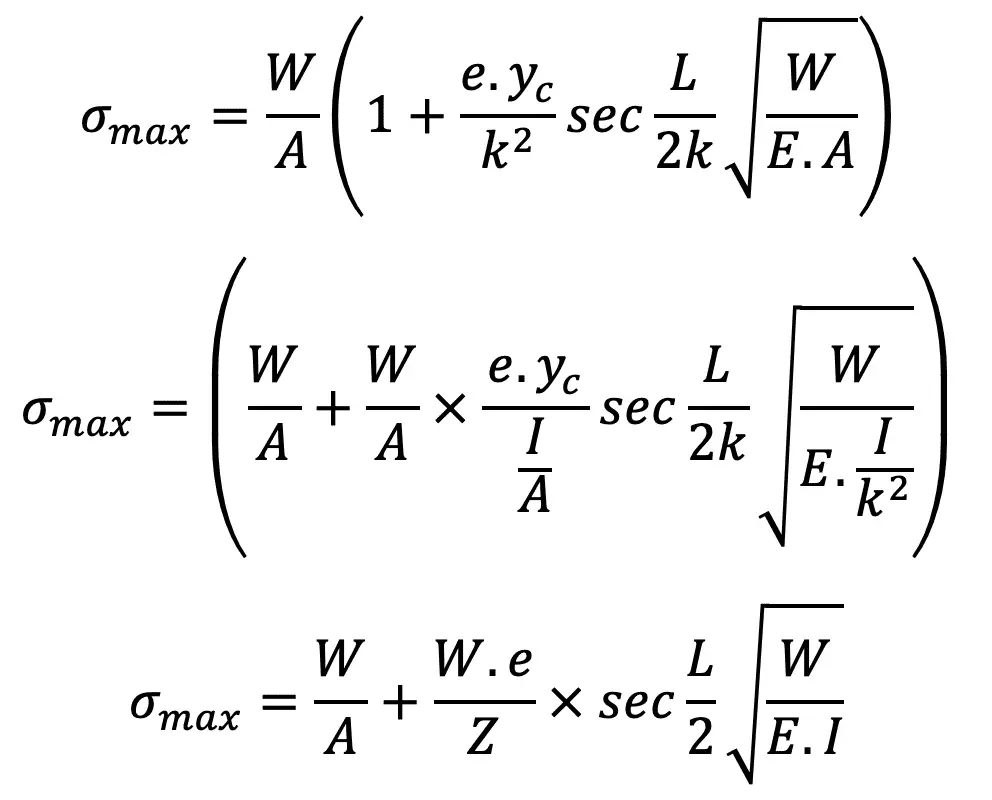
The following are the parameters that we have to determine in order to design a Piston rod for any Internal combustion Engine.

Let
p = Pressure acting on the piston,
D = Diameter of the piston,
d = Diameter of the piston rod,
W = Load acting on the piston rod,
W_cr = Buckling or crippling load = W × Factor of safety,
σ_t = Allowable tensile stress for the material of the rod,
σ_c = Compressive yield stress,
A = Cross-sectional area of the rod,
l = Length of the rod, and
k = Least radius of gyration of the rod section.

The only unknown parameter to design a piston rod is the piston rod diameter (d). With the diameter, we can design the Piston Rod. Many of the remaining above parameters will be available for us.

The diameter of the piston rod is obtained as discussed below:

1. When the length of the piston rod is small i.e. when the slenderness ratio (l / k) is less than 40, then the diameter of the piston rod may be obtained by equating the load acting on the piston rod to its tensile strength, i.e.

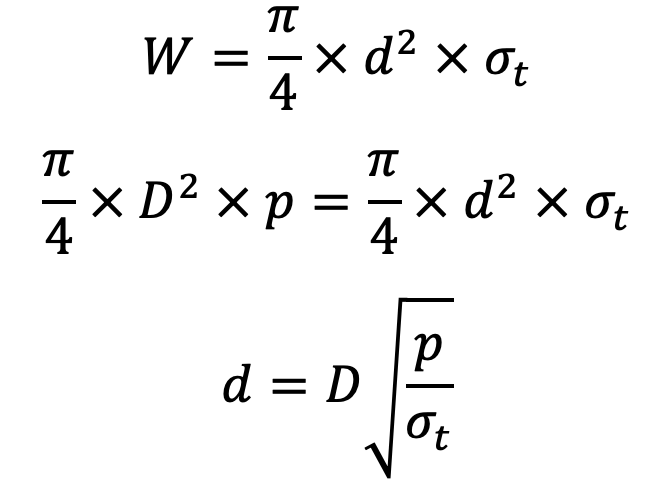
2. When the length of the piston rod is large, then the diameter of the piston rod is obtained by using Euler’s formula or Rankine’s formula. Since the piston rod is securely fastened to the piston and crosshead, therefore it may be considered a fixed end.

Euler’s formula is

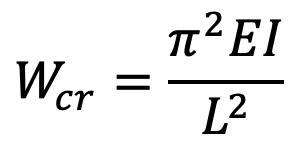
and Rankine’s formula is,

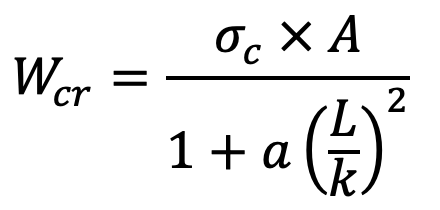
Example Problem to Design of a Piston Rod

Problem Statement: Calculate the diameter of a piston rod for a cylinder of 1.5 m diameter in which the greatest difference of steam pressure on the two sides of the piston may be assumed to be 0.2 N/mm². The rod is made of mild steel and is secured to the piston by a tapered rod and nut and to the crosshead by a cotter. Assume the modulus of elasticity as 200 kN/mm² and the factor of safety as 8. The length of the rod may be assumed as 3 meters.

Answer:

Piston Diamter D = 1.5m = 1500mm;
Pressure acting on the piston p = 0.2N/mm² ;
Modulus of elasticity E = 200 kN/mm² = 200×10³ N/mm²;
Length of Piston rod l = 3 m = 3000 mm

We know that the load acting on the piston,

W = (π/4) × D² × p = (π/4) × (1500)² × 0.2 = 353475N

Buckling load on the piston rod,

W_cr = W × Factor of safety = 353475 × 8 = 2.83 × 10⁶ N

Since the piston rod is considered to have both ends fixed, therefore from the following table,

Relation between equivalent length (L) and actual length (l ) of Column

End conditions	Relation between equivalent length (L) and actual length (l)
Both ends hinged	L = l
Both ends fixed	L = l / 2
One end fixed and other hinged	L = l /√2
One end fixed and other end free	L = 2 × l

The equivalent length of the piston rod, L = l/2 = 3000/2 = 1500 mm

Let
d = Diameter of the piston rod in mm
I = Moment of inertia of the cross-section of the rod = (π/64) × d⁴

According to Euler’s formula, buckling load (W_cr),

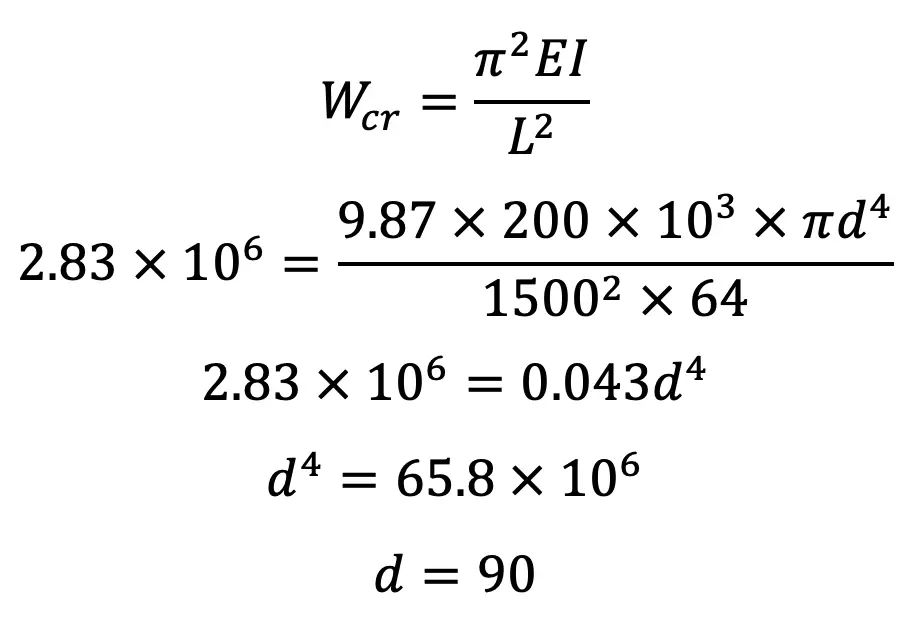
The piston rod diameter we get from Euler’s formula is 90mm. Now let us determine the same from Rankine’s formula as well and take the higher one.

According to Rankine’s formula, buckling load,

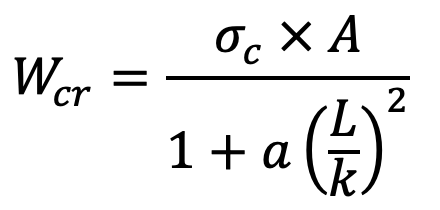
We know that for mild steel, the crushing stress,

σ_c = 320MPa = 320 N/mm²
a = 1/7500

and the least radius of gyration for the piston rod section,

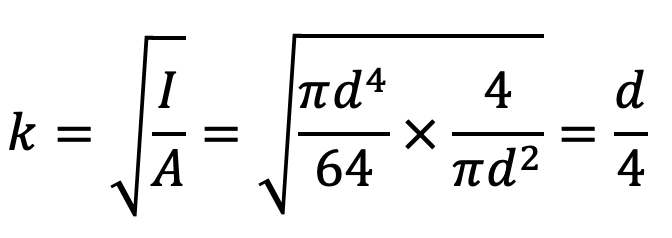
Substituting these values in the above Rankine’s equation, we have

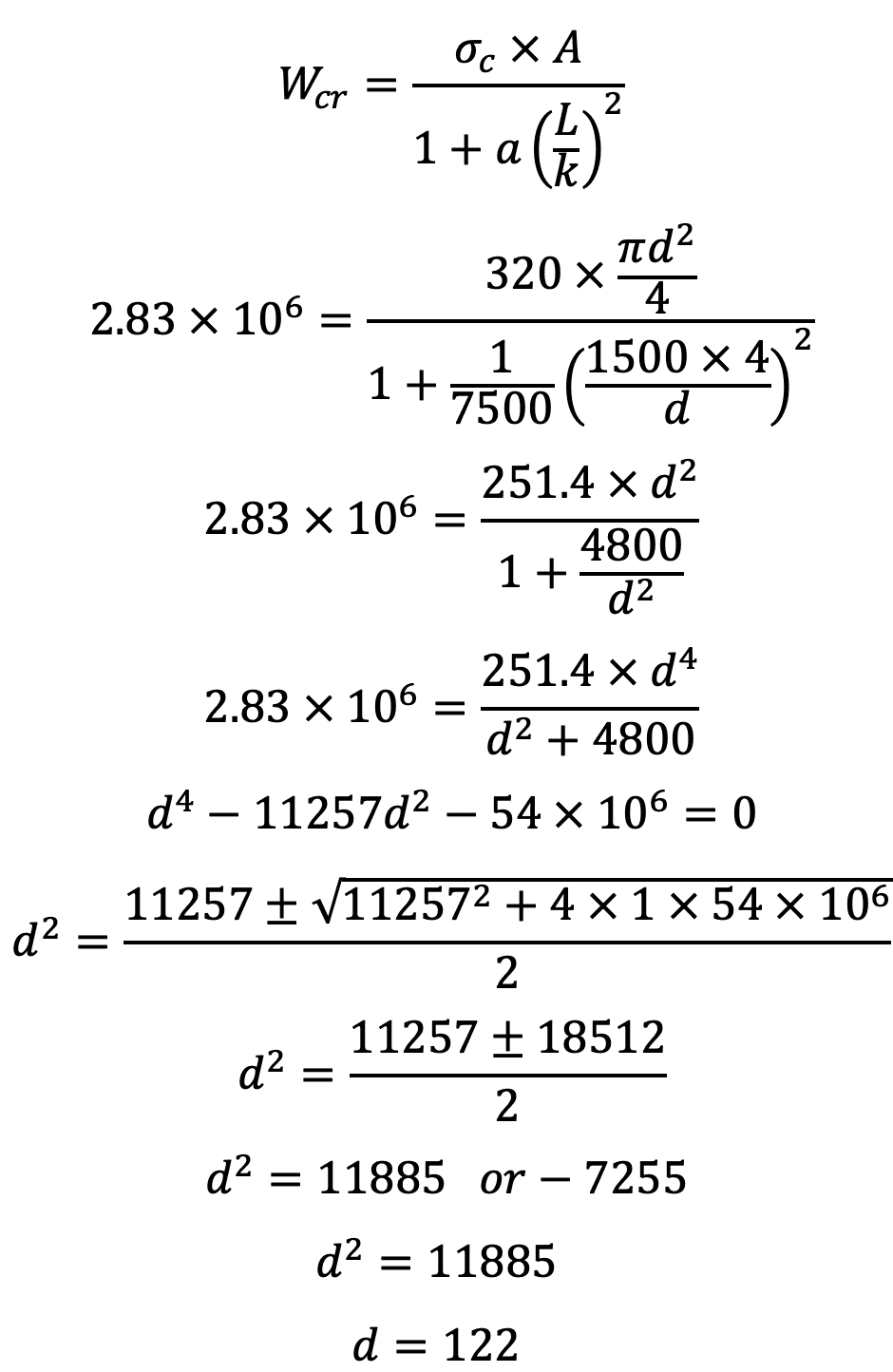
The piston rod diameter we get from Rankine’s formula is 122mm.

Taking the larger of the two values, we have a piston rod diameter is 122mm.

This is how we can design a Piston rod for an Internal combustion engine position. Let us know what you think about this article in the comment section below.