Usually, it is a common phenomenon observed in long columns failure due to buckling load and the short columns usually fail due to crushing load. The Rankine-Gordon formula assumes a combined failure mode which is combined buckling and crushing loads in columns. This common mode is known as the Rankine formula for columns. Hence, we can apply Rankine’s formula for all columns. Let us discuss more details.

Rankine’s Formula for Columns
We have already discussed that Euler’s formula gives correct results only for very long columns. Though this formula is applicable for columns, ranging from very long to short ones, yet it does not give reliable results. Prof. Rankine, after a number of experiments, gave the following empirical formula for columns.
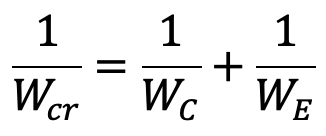
…. equation (a)
Where
Wcr = Crippling load by Rankine’s formula,
WC = Ultimate crushing load for the column = σc × A,
WE = Crippling load, obtained by Euler’s formula
- A little consideration will show, that the value of WC will remain constant irrespective of the fact whether the column is a long one or a short one.
- Moreover, in the case of short columns, the value of WE will be very high, therefore the value of 1/WE will be quite negligible as compared to 1/ WC.
- It is thus obvious, that Rankine’s formula will give the value of its crippling load (i.e. Wcr) approximately equal to the ultimate crushing load (i.e. WC).
- In the case of long columns, the value of WE will be very small, therefore the value of 1 / WE will be quite considerable as compared to 1 / WC.
- It is thus obvious, that Rankine’s formula will give the value of its crippling load (i.e. Wcr) approximately equal to the crippling load by Euler’s formula (i.e. WE ).
- Thus, we see that Rankine’s formula gives a fairly correct result for all cases of columns, ranging from short to long columns.
From equation (a), we know that
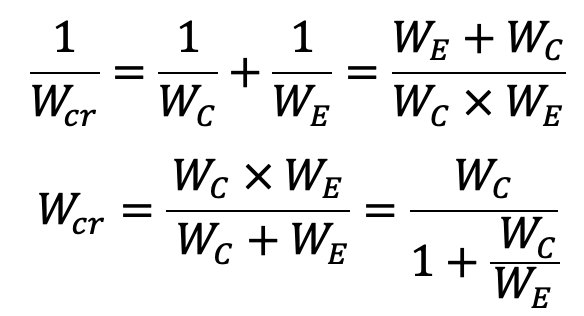
Now substituting the value of WC and WE in the above equation, we have
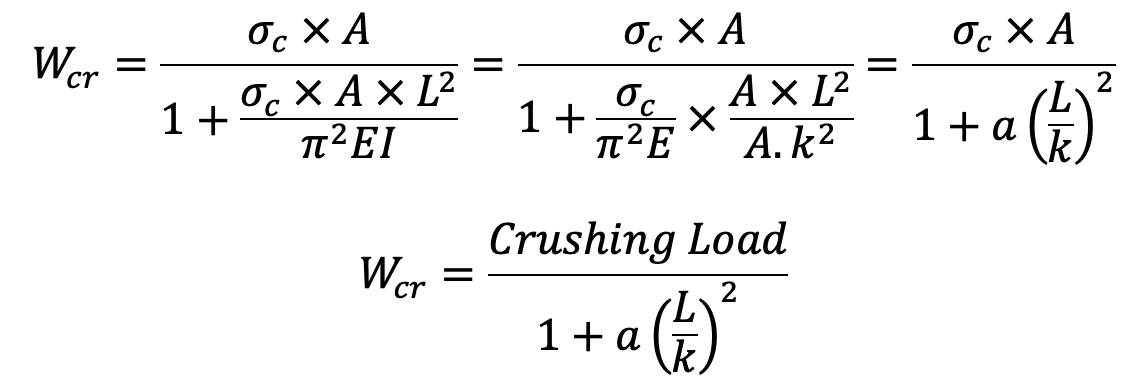
σc = Crushing stress or yield stress in compression,
A = Cross-sectional area of the column,
a = Rankine’s constant = σc / π2E
L = Equivalent length of the column,
k = Least radius of gyration.
The following table gives the values of crushing stress and Rankine’s constant for various materials.
Values of crushing stress (σc) and Rankine’s constant (a) for various materials.
| Material | σc in MPa | a = σc / π2E |
| Wrought iron | 250 | 1 / 9000 |
| Cast iron | 550 | 1 / 1600 |
| Mild steel | 320 | 1 / 7500 |
| Timber | 50 | 1 / 750 |
This is all about Rankine’s Formula for Columns. Let us know your thoughts on this article in the comment section below.

Leave a Reply