What is Euler’s Column Theory?

A machine part subjected to a vertical axial compressive force is called a column. it is also known as a pillar or stanchion. We see this vertical axial compressive force such as piston rods, valve push rods, connecting rods, screw jack, side links of toggle jack, etc. The first rational attempt, to study the stability of long columns, was made by Mr. Euler. He derived an equation, for the buckling load of long columns based on the bending stress. Let us study Euler’s Column Theory and its assumptions. Furthermore, we will discuss Euler’s Formula, the limitations of Euler’s formula, the crippling load of a column, and determine the equivalent Length of a Column.

Euler’s Column Theory

As we mentioned that the first rational attempt to study the stability of long columns, was made by Mr. Euler. He derived an equation, for the buckling load of long columns based on the bending stress. While deriving this equation, the effect of direct stress is neglected.

This may be justified with the statement, that The direct stress induced in a long column is negligible compared to the bending stress.

It may be noted that Euler’s formula cannot be used in the case of short columns, because the direct stress is considerable, and hence cannot be neglected.

Short columns are the ones that have lengths < 8 times their diameter whereas the long columns that have lengths > 30 times their diameter.

Assumptions in Euler’s Column Theory

The following simplifying assumptions are made in Euler’s column theory :

1. Initially, the column is perfectly straight, and the load applied is truly axial.
2. The cross-section of the column is uniform throughout its length.
3. The column material is perfectly elastic, homogeneous, and isotropic, and thus obeys Hooke’s law.
4. The length of the column is very large compared to its cross-sectional dimensions.
5. The shortening of the column, due to direct compression (being very small) is neglected.
6. The failure of the column occurs due to buckling alone.
7. The weight of the column itself is neglected.

Euler’s Formula

According to Euler’s theory, the crippling or buckling load (W_cr) under various end conditions is represented by a general equation,

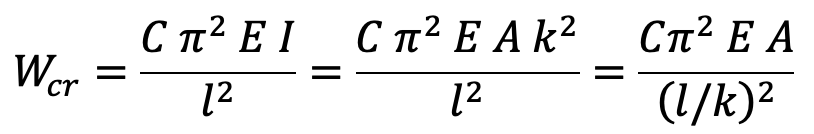
Where
E = Modulus of elasticity or Young’s modulus for the material of the column,
A = Area of cross-section,
k = Least radius of gyration of the cross-section,
l = Length of the column, and
C = Constant, representing the end conditions of the column or end fixity coefficient.

The following table shows the values of the end fixity coefficient (C) for various end conditions.

Values of end fixity coefficient (C)

End conditions	End fixity coefficient (C)
Both ends hinged	1
Both ends fixed	4
One end fixed and other hinged	2
One end fixed and other end free	0.25

1. The vertical column will have two moments of inertia (viz. I_xx and I_yy). Since the column will tend to buckle in the direction of the least moment of inertia, therefore the least value of the two moments of inertia is to be used in the relation.
2. In the above formula for crippling load, we have not taken into account the direct stresses induced in the material due to the load which increases gradually from zero to the crippling value. As a matter of fact, the combined stresses (due to the direct load and slight bending), reaches its allowable value at a load lower than that required for buckling and therefore this will be the limiting value of the safe load.

Slenderness Ratio

In Euler’s formula, the ratio l / k is known as the slenderness ratio. It may be defined as the ratio of the effective length of the column to the least radius of the gyration of the section.

It may be noted that the formula for crippling load, in the previous article, is based on the assumption that the slenderness ratio l / k is so large, that the failure of the column occurs only due to bending, the effect of direct stress (i.e. W / A) being negligible.

Limitations of Euler’s Formula

We have discussed that the general equation for the crippling load is

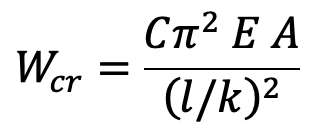
Crippling stress,

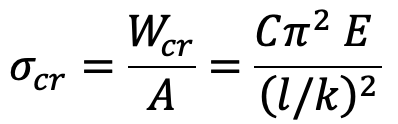
A little consideration will show that the crippling stress will be high when the slenderness ratio is small. We know that the crippling stress for a column cannot be more than the crushing stress of the column material. It is thus obvious that Euler’s formula will give the value of the crippling stress of the column (equal to the crushing stress of the column material) corresponding to the slenderness ratio.

Now consider a mild steel column.

We know that the crushing stress for mild steel is 330 N/mm² and Young’s modulus for mild steel is 0.21 × 10⁶ N/mm².

Now equating the crippling stress to the crushing stress, we have

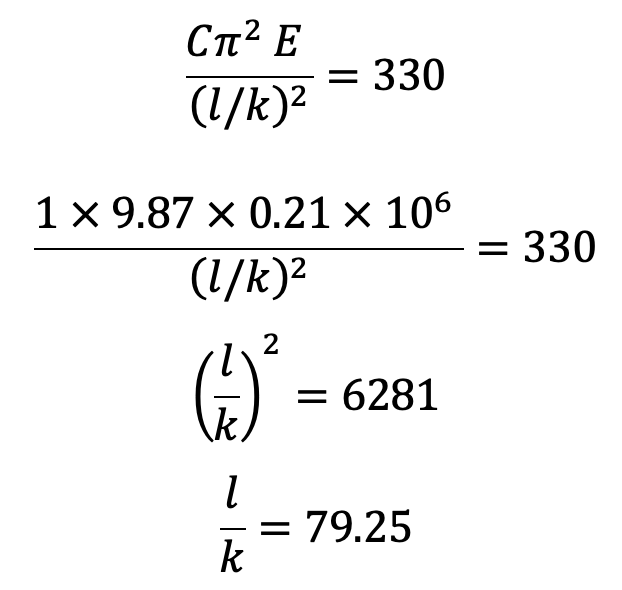
Hence if the slenderness ratio is less than 80, Euler’s formula for a mild steel column is not valid.

Sometimes, the columns whose slenderness ratio is more than 80, are known as long columns, and those whose slenderness ratio is less than 80 are known as short columns. It is thus obvious that Euler’s formula holds good only for long columns.

Equivalent Length of a Column

Sometimes, the crippling load according to Euler’s formula may be written as

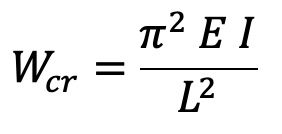
where L is the equivalent length or effective length of the column. The equivalent length of a given column with given end conditions is the length of an equivalent column of the same material and cross-section with hinged ends to that of the given column. The relation between the equivalent length and actual length for the given end conditions is shown in the following table.

Relation between equivalent length (L) and actual length (l ) of Column

End conditions	Relation between equivalent length (L) and actual length (l)
Both ends hinged	L = l
Both ends fixed	L = l / 2
One end fixed and other hinged	L = l /√2
One end fixed and other end free	L = 2 × l

This is all about Euler’s Column Theory and its assumptions, Euler’s Formula, the limitations of Euler’s formula, the crippling load of a column, and determining the equivalent Length of a Column. Let us know what you think about this article in the comment section below.