What is the Gas Constant (R)?

We have discussed the physical properties of Fluids in the previous article. Fluids are either liquids or gases. A Gas constant or Universal molar Gas constant is used to determine the behaviour of a gas under the theoretical conditions. It is denoted by R. Let us discuss more details on the Gas constant.

As we mentioned already the Fluids are either liquids or gases. AS we know already that the only gases are the compressible fluids. So the thermodynamic properties of Gases play a very important role while understanding the behaviour of the gases.

Pressure and Temperature Relationship of Gas

With the change in pressure and temperature of the gas, there will be a huge change in the Density of the gas.

The relationship between the pressure, temperature and specific volume of the gas given by the equation of state is

pV = RT

p/ρ = RT

Where
p= Absolute pressure of a gas in N/m²
V = Specific volume = 1/ρ
R = Gas constant
T = Absolute temperature in °K
ρ = Density of a gas

Let us determine the dimensions of the Gas constant

Dimension of Gas constant (R)

The gas constant, R, depends upon the particular gas. The dimension of R can be obtained from the equation the above equation

p/ρ =RT
R = p/ρT

(i) In MKS system the units of the Gas constant are

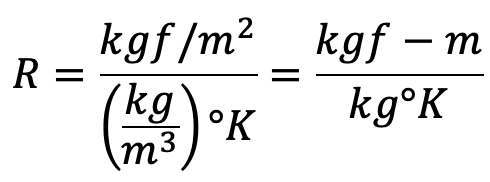
(ii) In SI units the p is expressed in N/m²

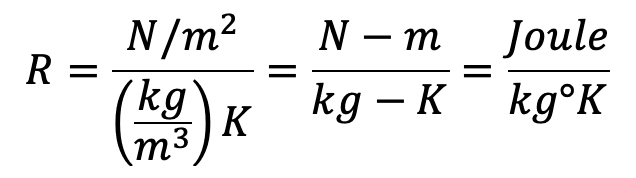
The Gas constant for Air is

R in MKS units = 29.3 kgf-m/kg°K
R in SI units = 29.3 × 9.81 kgf-m/kg°K = 287 J/kg-K

While understanding the behaviour of the gas, it is very important to understand what is the isothermal process and the adiabatic process.

Isothermal Process

If the changes in the density occur at a constant temperature, then the process is called the isothermal and the relation between the pressure and the density is given by

p/ρ = Constant

Adiabatic Process

If the change in density occurs with no heat exchange to and from the gas, the process is called adiabatic. And if no heat is generated within the gas due to friction, the relationship between pressure and density is given by

p/ρ^k = Constant

where k = Ratio of specific heat of a gas at constant pressure and constant volume = 1.4 for air.

Universal Gas Constant

Let
m = Mass of gas in kg
V = Volume of gas of mass m
p = Absolute pressure
T = Absolute temperature

Then, we have

pV = mRT

Where R = Gas constant

This equation can be made universal, i.e., applicable to all gases if it is expressed on a mole basis.

Let
n = number of moles in the volume of a gas
V = Volume of the gas
M = Mass of the gas molecules / Mass of a hydrogen atom
m = Mass of gas in kg

Then, we have. n × M = m

Substituting the value of m in the above equation, we get

pV = n × M × RT

The product M × R is called the universal gas constant and is equal to 848 (kgf-m)/(kg-mole°K) in MKS units and 8314 J/(kg-mole K) in SI units.

One kilogram mole is defined as the product of one kilogram mass of the gas and its molecular weight.

Let us solve one example problem to find the gas constant and the density of the gas.

Problem Statement 1: A gas weighs 16 N/m³ at 25°C and at an absolute pressure of 0.25 N/mm². Determine the gas constant and density of the gas.

Answer:

Weight density,W = 16 N/m³

Temperature,t = 25°C
T = 273 + t = 273 + 25 = 288°K

Given Absolute pressure
p = 0.25 N/mm²
p = 0.25 x 10⁶ N/m²
p = 25 x 10⁴ N/m²

(i) Using relation w = ρg, density is obtained as

ρ = g/w
ρ = 16/9.8
ρ = 1.63 kg/m³

(ii) Using relation p/ρ = RT, we can obtain the gas constant

R = p/ρT
R = (25 x 10⁴)/(1.63)×288
R = 532.55 Nm/kg K

Problem Statement 2: A cylinder of 0.6 m³ in volume contains air at 50°C and 0.3 N/mm² absolute pressure. The air is compressed to 0.3 m³. Find following.
(i) Pressure inside the cylinder assuming the isothermal process
(ii) Pressure and temperature assuming adiabatic process. Take k = 1.4.

Answer:

Initial Volume V₁ = 0.6m³
Temperature t₁ = 50°C (T₁ = 273 + 50 = 323°K)
Pressure P₁ = 0.3 N/mm² = 0.3 x 10⁶ N/m² = 30 x 10⁴ N/m²
Final volume V₂ = 0.3 m³
k = 1.4

(i) Isothermal Process

Isothermal process equation p/ρ = Constant or pV = constant

p₁V₁ = p₂V₂
p₂ = p₁V₁ / V₂
p₂ = (30 × 10⁴ ×0.6) / 0.3
p₂ = 0.6 × 10⁶N/m²
p₂ = 0.6 N/mm²

(ii) Adiabatic Process

For Pressure:

Adiabatic process equation p/ρ^k = Constant or pV^k = constant

p₁V^k₁ = p₂V^k₂
p₂ = p₁ (V^k₁ / V^k₂)
p₂ = 30 × 10⁴ × (0.6/0.3)^1.4
p₂ = 30 × 10⁴ × (2)^1.4
p₂ = 0.791 × 10⁶ N/m²
p₂ = 0.791 N/mm²

For temperature:

using the relation we have pV = RT , we get

p = RT/V

From the adiabatic relation pV^k = constant, we can substitute the above p value, we get

pV^k = constant
(RT/V) × V^k = constant
RTV^k-1 = Constant

We know R is also Constant,

TV^k-1 = Constant
T₁V^k-1₁ = T₂V^k-1₂
T₂ = T₁ × (V^k-1₁ / V^k-1₂)
T₂ = 323 (0.6/0.3)^1.4-1.0
T₂ = 323 × 2^0.4
T₂ = 426.2°K

t₂ = 426.2 – 273
t₂ = 153.2°C

Conclusion

We have discussed the units of Gas constant and also derivation for the Universial Gas constant. We solved two example problems on the Gas constant and the calculating fluid density with the gas constant., Let us know what do you think about this article in the comment section below.