In General, the shaft is comprised of multiple cross-sectional diameters with different lengths. Sometimes it is necessary to assume the shaft as a uniform diameter and length for some calculations such as finding the natural frequency. In such cases, we have to replace the different cross-section diameters with the equivalent shaft of uniform diameter. Which will discuss how we can construct such data of torsionally equivalent shaft for calculation purposes.

Torsionally Equivalent Shaft
Consider a shaft of varying cross-sections as shown in below fig. Let this shaft is replaced by an equivalent shaft of uniform diameter d and length l as shown figure.
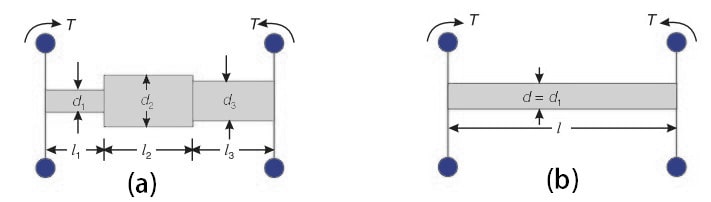
These two shafts must have the same total angle of a twist when equal opposing torques T are applied at the opposite ends.
- d1, d2 and d3 = Diameters for the lengths l1, l2 and l3 respectively,
- θ1, θ2 and θ3 = Angles of twist for the lengths l1, l2 and l3 respectively,
- θ = Angle of twist for the diameter d and length l,
- J1, J2 and J3 = Polar moment of inertia for the shaft of diameters d1, d2 and d3 respectively.
Since the total angle of the twist of the shaft is equal to the sum of the angle of twists of the different lengths.
θ = θ1 + θ2 + θ3
From the torsion Equation
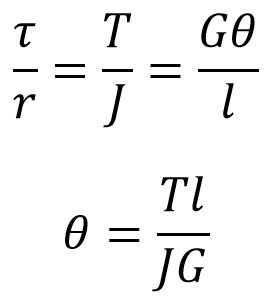
Where
- τ = Shear stress (MPa)
- r = Radius of the shaft (mm)
- T = Torque (Nm)
- J = Polar moment of inertia
- G = Modulus of rigidity (MPa)
- θ = Angle of twist (rad)
- l = length of the shaft
We can write θ = θ1 + θ2 + θ3 as following
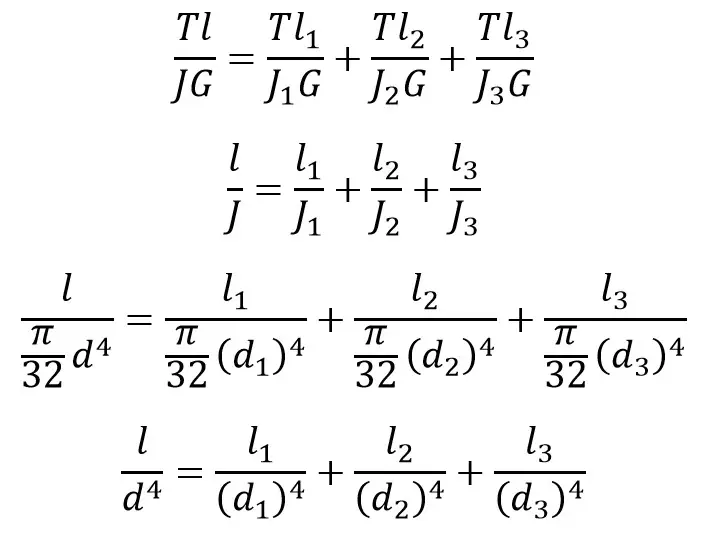
As we want to make the multiple cross-sectional shafts into a uniform diametral shaft, so we have to assume that the diameter d of the equivalent shaft should be equal to one of the diameters of the actual shaft. So we can assume d = d1
Substitute
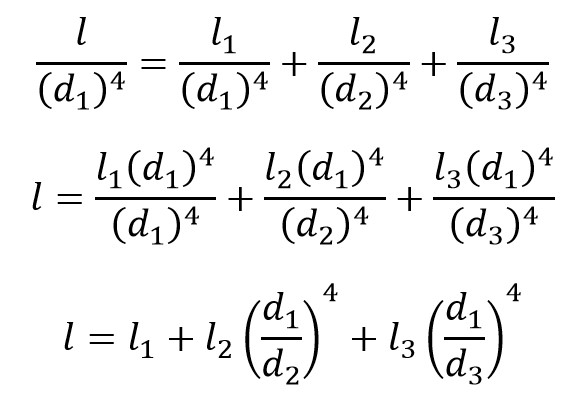
From this expression, we can evaluate the length of the torsionally equivalent shaft.
Conclusion
We have discussed how the torsionally equivalent shaft diameter and the length can be evaluated from the shaft of varying cross-sectional diameters. If you have further thoughts on this topic, please let us know in the comment section below.
Check Shaft stiffness Calculator, Shaft/flange inertia calculator

Leave a Reply