We know what is a mass moment of inertia, it is a resistance force of a physical object to any change in its state of motion, But what is a polar moment of inertia?
By definition Polar Moment of Inertia is a measure of resistibility of a shaft against the twisting.
Polar moment of inertia is required to calculate the twist of the shaft when the shaft is subjected to the torque.
It is different from the moment of inertia. where inertia is resistance to change in its state of motion or velocity. Which is directly proposal to the mass.
Example: Consider a beam of length L and a rectangular cross-section having b×h
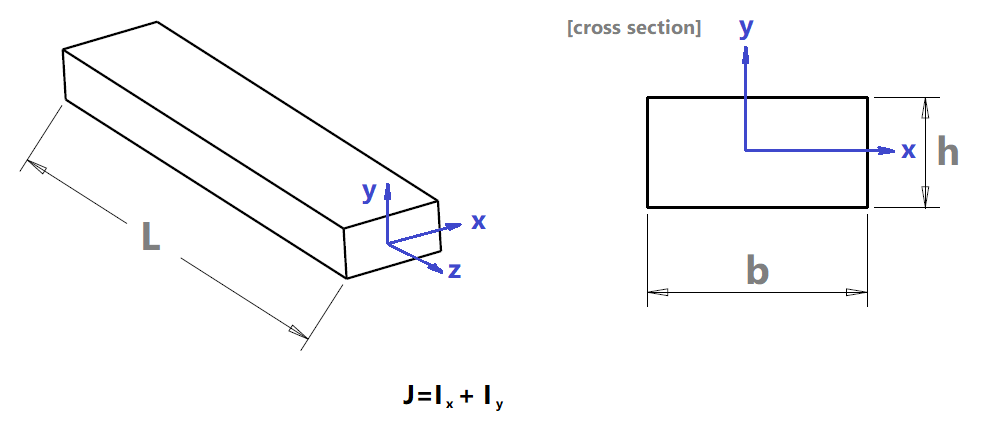
Where the three axis X, Y, Z represented.
X-axis along the breadth of the rectangular cross-section.
Y-axis along the height of the rectangular cross-section.
Z-axis along the length of the beam.
The moment of inertia about the X-axis and Y-axis are bending moments, and the moment about the Z-axis is a polar moment of inertia(J).
Polar moment of inertia is equal to the sum of inertia about X-axis and Y-axis
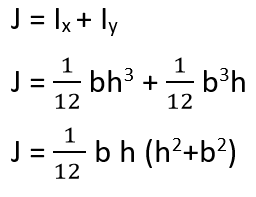
This is for the Rectangular cross-section beams.
Polar Moment of Inertia for Circular Cross-section
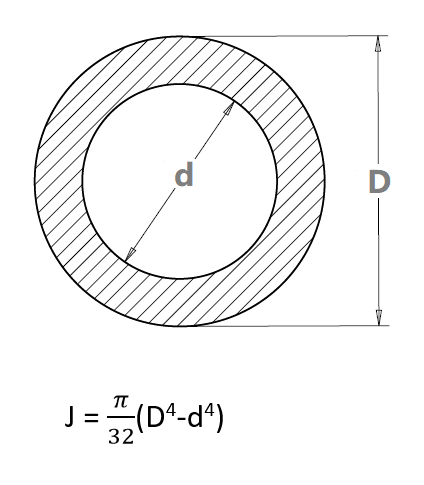
For solid circular shaft d value will be zero in the above formula.
Check how this polar moment of inertia is used to calculate the shaft stiffness calculator
Polar Moment of Inertia for Triangular Cross-section
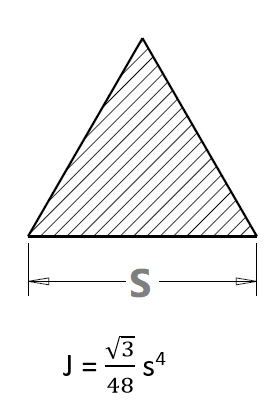
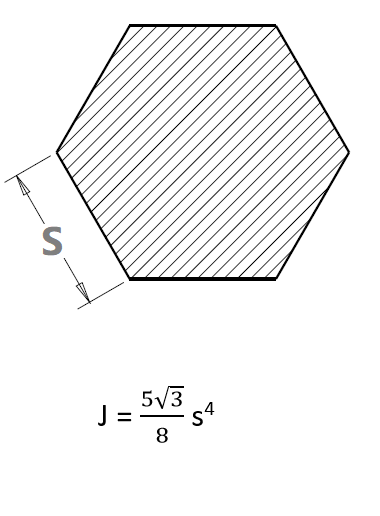
Polar Moment of Inertia for Hexagonal Cross-section
Check this Mass moment of Inertia Calculator!

Was really helpful, thanks for the info