The study of Flow of Viscous Fluid in a Pipe

We have been discussing kinematics and the dynamics of the fluid. In this article, we will discuss the study of the flow of the Viscous fluid in a pipe. The Fluids that have higher viscosity are known as viscous fluids and they will have very less velocity flow. The most common and general examples of viscous fluids are honey, grease and oil. Let us discuss more details such as the Shear stress distribution of viscous fluid, viscous fluid velocity distribution and the drop of the pressure for a given length of a pipe.

Viscous Fluid Flow

As we already mentioned Fluids that have higher viscosity are known as viscous fluids and they will have very less velocity flow. At low velocity the fluid moves in layers. Each layer of fluid slides over the adjacent layer.

Due to the relative velocity between two layers the velocity gradient du/dy exists and hence the shear stress acts on the layer will be

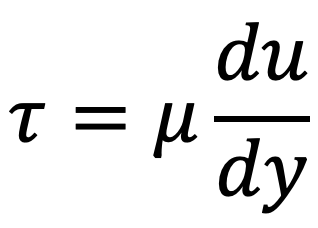
Following are these different scenarios, we shall be discussing to study the flow of viscous fluid

1. The flow of viscous fluid through a circular pipe
2. The flow of viscous fluid between two parallel plates
3. Kinetic energy correction and momentum correction factors
4. Power absorbed in viscous flow through
   • Journal bearings
   • Foot-step bearings
   • Collar bearings

In this article, we will discuss the flow of viscous fluid through a circular pipe in a detailed manner with the viscous fluid velocity distribution and the drop of the pressure for a given length of a pipe.

Flow of Viscous Fluid Through Circular Pipe

For the flow of viscous fluid through a circular pipe, the velocity distribution across a section, the ratio of maximum velocity to average velocity, the shear stress distribution and the drop of pressure for a
given length is to be determined.

The flow through the circular pipe will be viscous or laminar if the Reynolds number (R) is less than 2000. The expression for Reynold number is given by

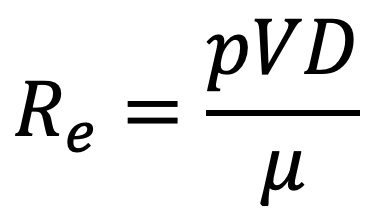
where
ρ = Density of fluid flowing through the pipe
V = Average velocity of the fluid
D = Diameter of pipe
M = Viscosity of fluid

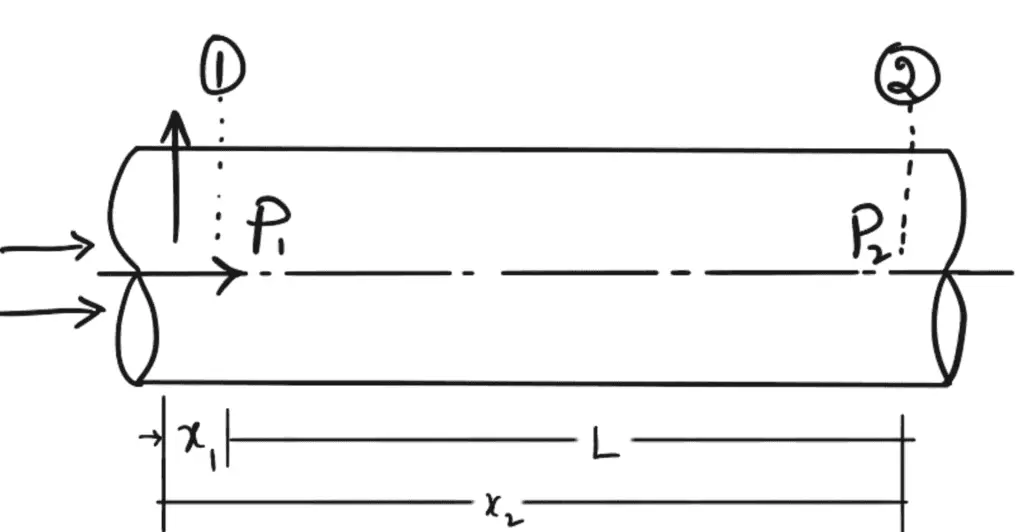
Let us consider a horizontal pipe of radius R.

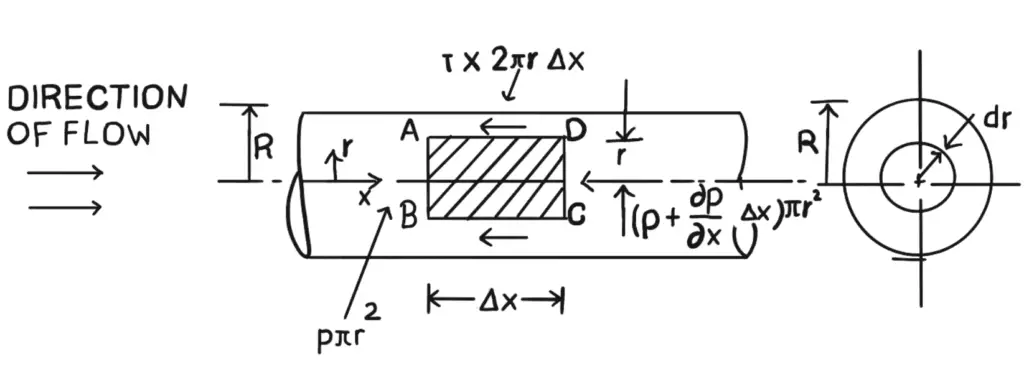
The viscous fluid is flowing from left to right in the pipe as shown in the above figure.

Shear stress distribution of Viscous Fluid in pipe

Consider a fluid element of radius r, sliding in a cylindrical fluid element of radius (r + dr).

Let the length of the fluid element be Δx. If ‘p’ is the intensity of pressure on the face AB, then the intensity of pressure on the face CD will be

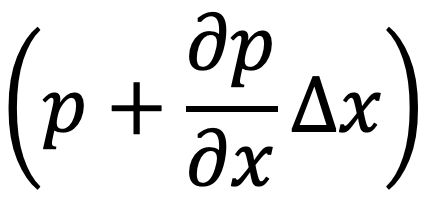
Then the forces acting on the fluid element are as follows

1. The pressure force p × πr on face AB.
2. The pressure force will be on the face CD is as follows

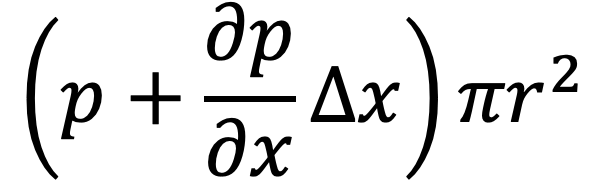
3. The shear force, 𝜏 × 2π r Δx on the surface of the fluid element. As there is no acceleration, hence the summation of all forces in the direction of flow must be zero i.e

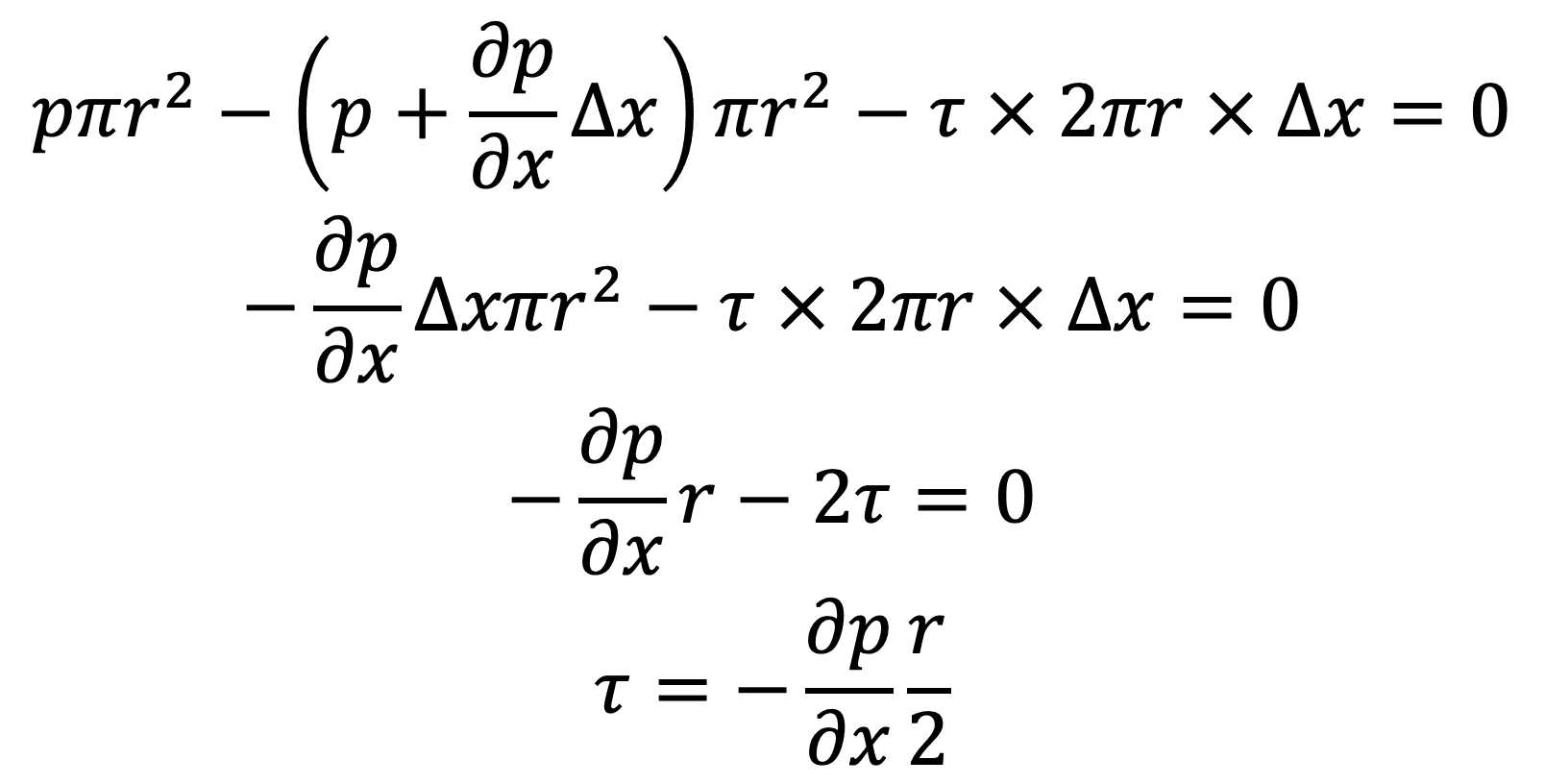
The shear stress 𝜏 across a section varies with ‘r’ as ∂p/∂x across a section is constant.

Hence shear stress distribution across a section is linear as shown in the following figure.

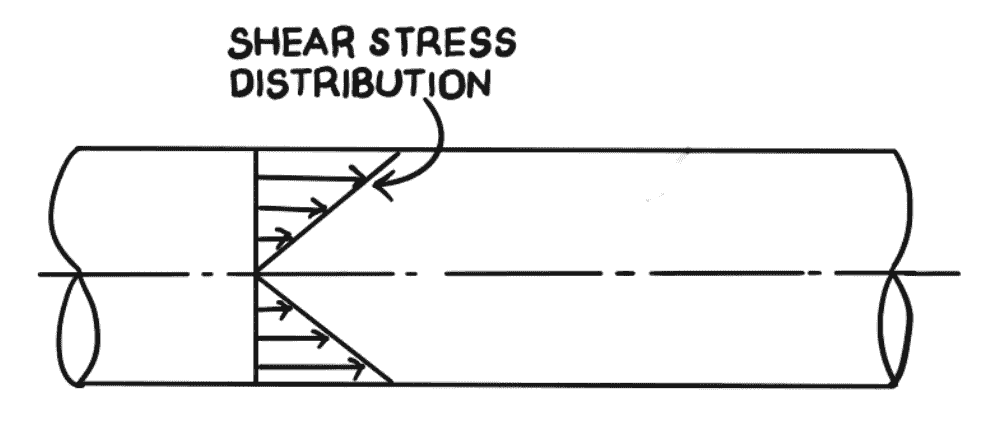
Equation (a) can be used to calculate the shear stress distribution of viscous fluid flowing along a circular pipe

Velocity Distribution of Viscous Fluid in pipe

To obtain the velocity distribution across a section, the value of shear stress as mentioned below is substituted in the above equation(a).

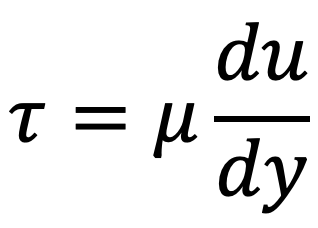
But in the above relation, y is measured from the wall, hence

y = R- r
dy = -dr

The above shear stress equation becomes as follows

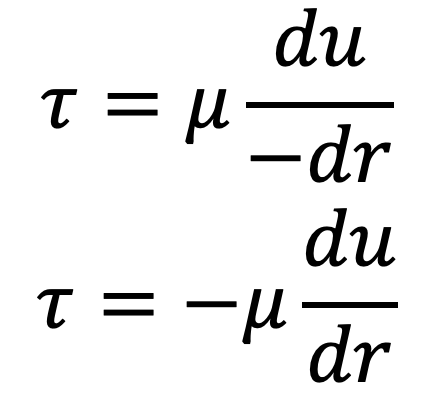
Substituting this value in the above equation (a), we get

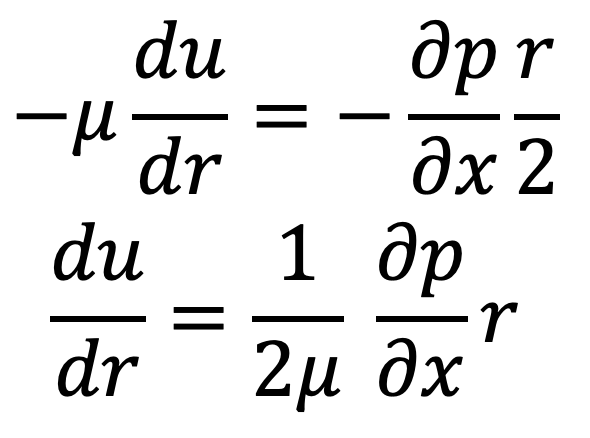
Integrating this equation on both sides with respect to ‘r’, we get

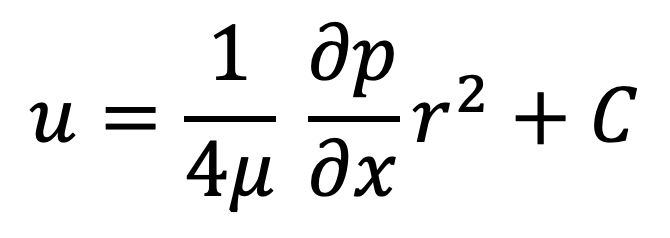
where C is the constant of integration and its value is obtained from the boundary condition that at
r = R
u = 0

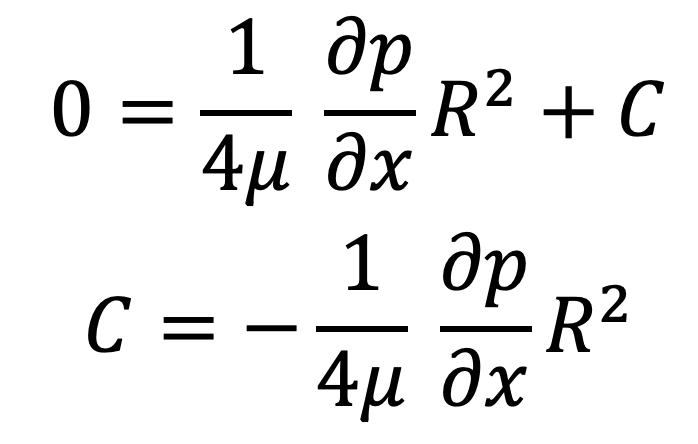
Substituting this value of C in equation (b), we get

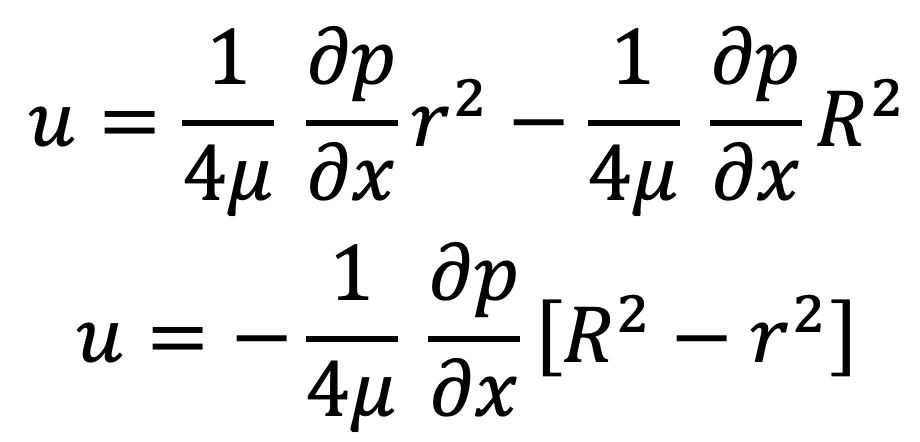
In equation (c), values of u and ∂p/∂x are constant, which means the velocity, u varies with the square of r.

Thus equation (c) is an equation of a parabola. This shows that the velocity distribution across the section of a pipe is parabolic.

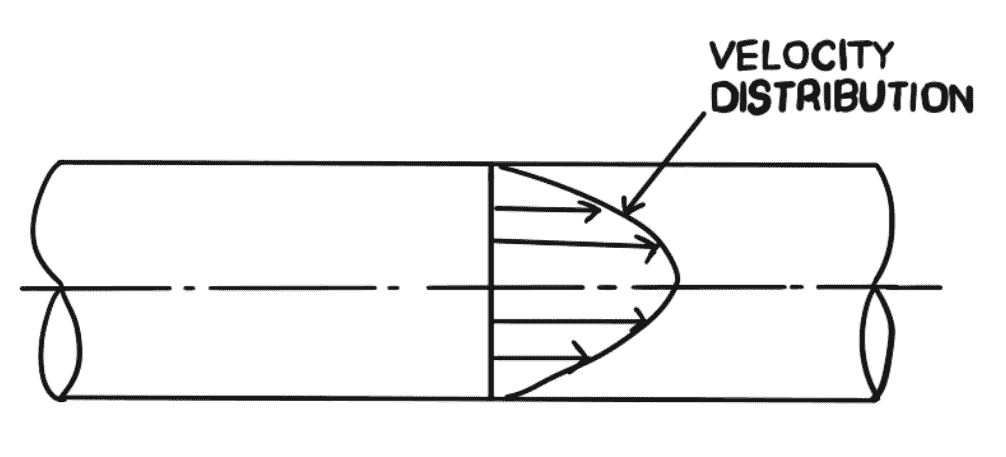
This velocity distribution is shown in the above figure right part.

Ratio of Maximum Velocity to Average Velocity

The velocity is maximum when r = 0 in equation (c). Thus maximum velocity, U_max is obtained as

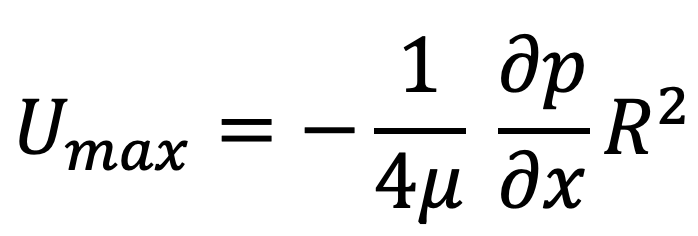
The average velocity, u, is obtained by dividing the discharge of the fluid across the section by the
area of the pipe (πR²).

The discharge (Q) across the section is obtained by considering the flow through a circular ring element of radius r and thickness dr as shown in the following.

The fluid flowing per second through this elementary ring is given as follows

dQ = Velocity at a radius r × area of the ring element
dQ = u × 2π r dr

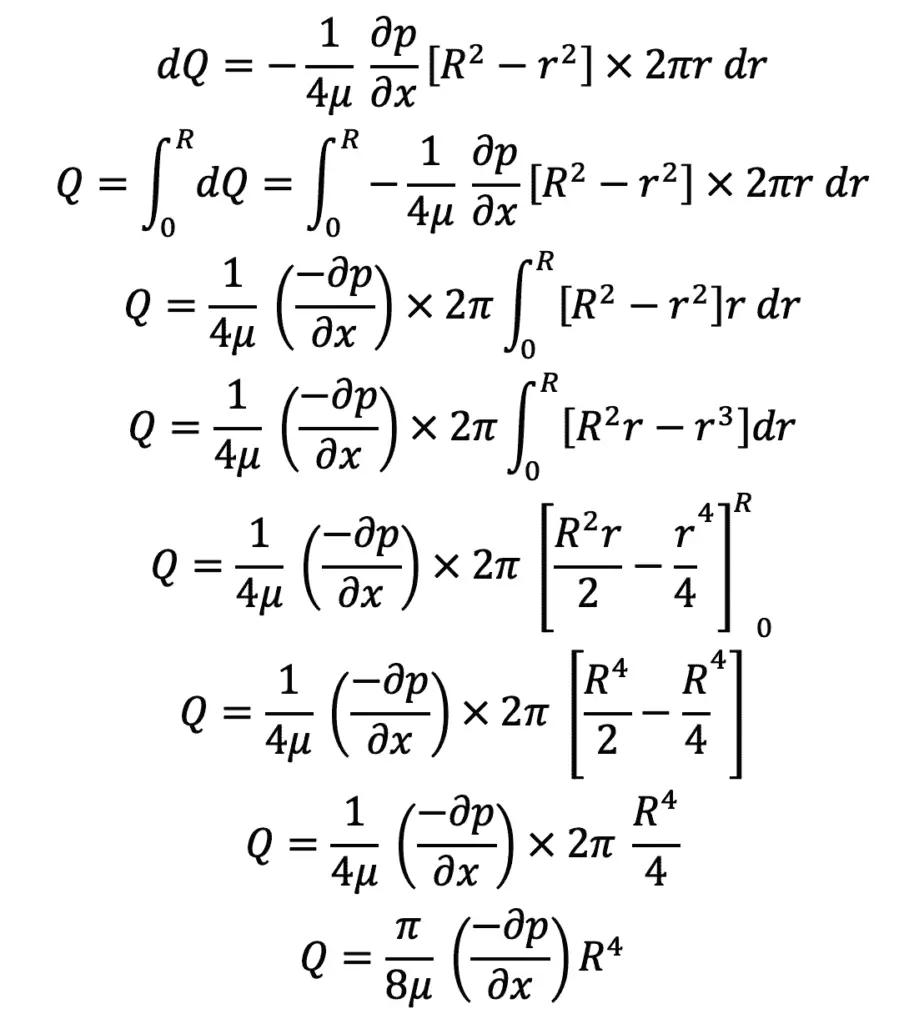
Average velocity is

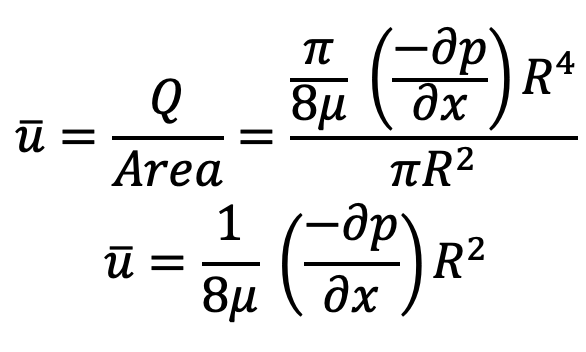
Divide the equation (d) with the equation (e)

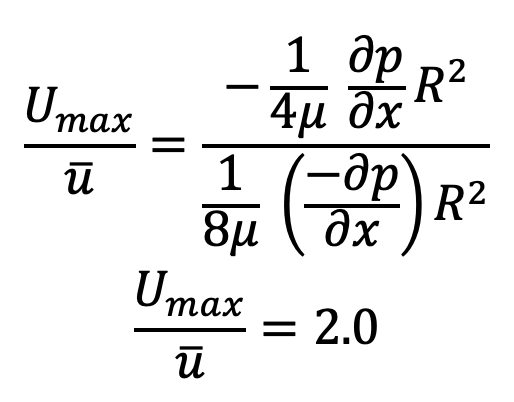
The ratio of maximum velocity to average velocity = 2.0.

Drop of Pressure for a given Length (L) of a pipe

From equation (e), we have

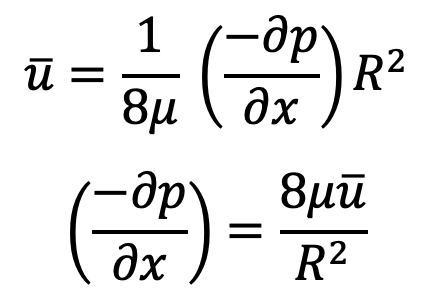
Integrating the above equation with respect to x, we get

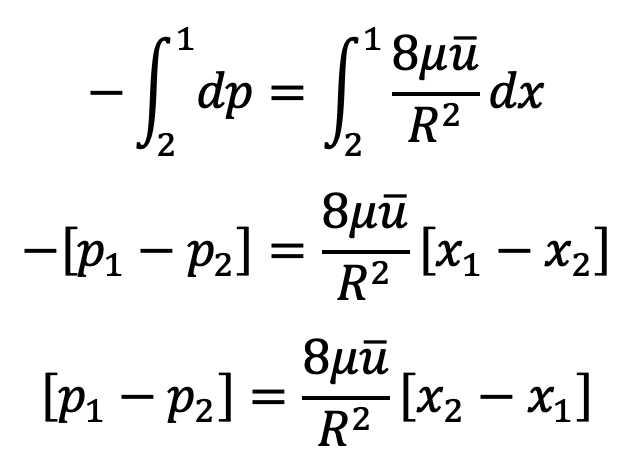
(x₂-x₁) = L and R = D/2, we get

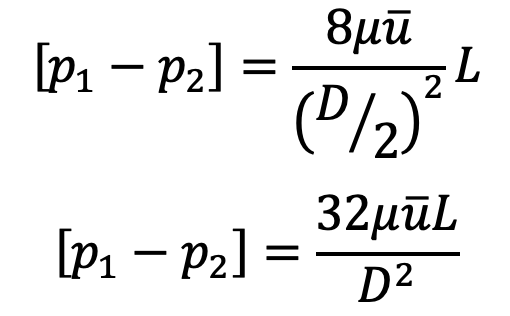
Loss of pressure head

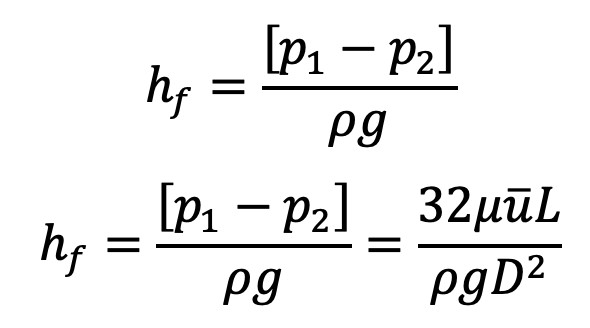
This equation is called Hagen Poiseuille Formula.

This is all about the flow of viscous fluid in a pipe. The Study of Viscous Fluid between two Parallel Plates and Kinetic energy correction and momentum correction factors has been discussed in this next article. Let us know what you think about this article in the comment section below.