We have been discussing kinematics and the dynamics of the fluid. In this article, we will discuss Power Absorbed In Viscous Flow. The Fluids that have higher viscosity are known as viscous fluids and they will have very less velocity flow. The most common examples of viscous fluid are honey, grease and oil. Let us discuss more details of the Power Absorbed In Viscous Flow for different journal bearings such as Journal Bearings, Foot-Step Bearing and Collar Bearing.

Viscous Flow
As we already mentioned Fluids that have higher viscosity are known as viscous fluids and they will have very less velocity flow. At low velocity the fluid moves in layers. Each layer of fluid slides over the adjacent layer.
Due to the relative velocity between two layers the velocity gradient du/dy exists and hence the shear stress acts on the layer will be
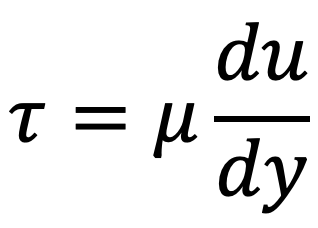
Following are these different scenarios, we shall be discussing to study the flow of viscous fluid
- The flow of viscous fluid through a circular pipe
- The flow of viscous fluid between two parallel plates
- Kinetic energy correction and momentum correction factors
- Power absorbed in viscous flow through
- Journal bearings
- Foot-step bearings
- Collar bearings
In the previous articles, we have already discussed the first 3 cases (The study of the Flow of Viscous Fluid in a Pipe, between two Parallel Plates and the Kinetic energy correction and momentum correction factors)(Please click the above links to read more about them)
In this article, we will discuss more details of the Power Absorbed In Viscous Flow for different journal bearings.
Power Absorbed In Viscous Flow
For the lubrication of the machine parts, oil is used. As we mentioned above oil is one of the viscous fluids which is used in bearings and is an example of viscous flow. If a highly viscous oil is used for lubrication of bearings, it will offer great resistance and thus a greater power loss will take place. But if light oil is used, a required film between the rotating part and stationary metal surface will not be possible. Hence, the wear of the two surfaces will take place. Hence an oil of correct viscosity should be used for lubrication.
We will determine the power required to overcome the viscous resistance for the following cases.
- Viscous resistance of Journal Bearings
- Viscous resistance of Foot-step Bearings
- Viscous resistance of Collar Bearings
1. Viscous Resistance of Journal Bearings
Let us consider a shaft of diameter D rotating in a journal bearing.
- The clearance between the shaft and journal bearing is filled with viscous oil.
- The oil film in contact with the shaft rotates at the same speed as that of the shaft while the oil film in contact with the journal bearing is stationary.
- Thus the viscous resistance will be offered by the oil to the rotating shaft.
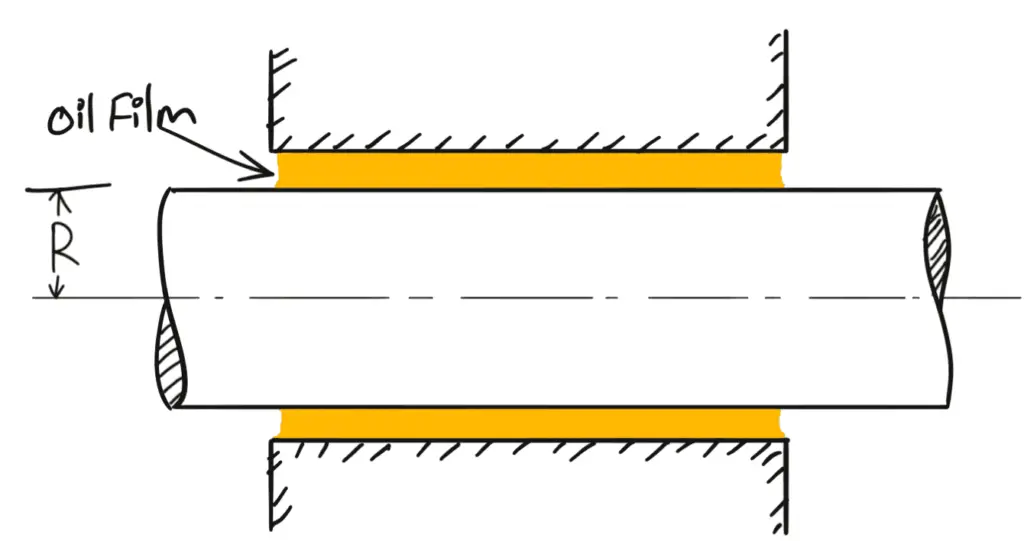
Let us say
Speed of shaft in r.p.m. = N
The thickness of oil film = t
Length of oil film = L
The Angular speed of the shaft will be
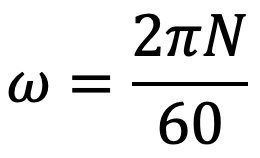
The Tangential speed of the shaft will be
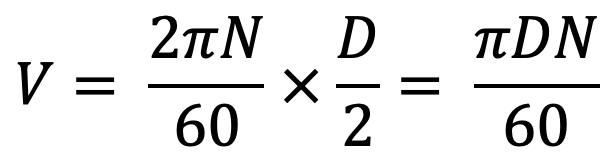
The shear stress in the oil is given by
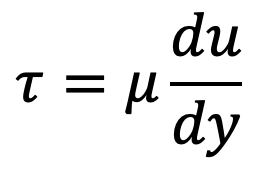
As the thickness of oil film is very small, the velocity distribution in the oil film can be assumed as
linear
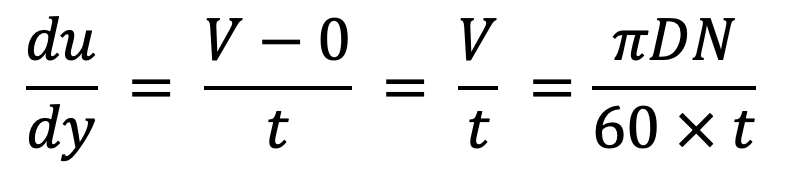
Let us substitute this value in the above shear stress equation, we get
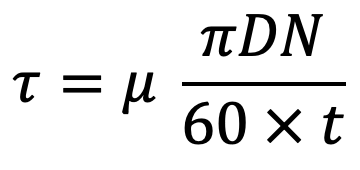
Shear force or viscous resistance = 𝜏 × Area of the surface of the shaft
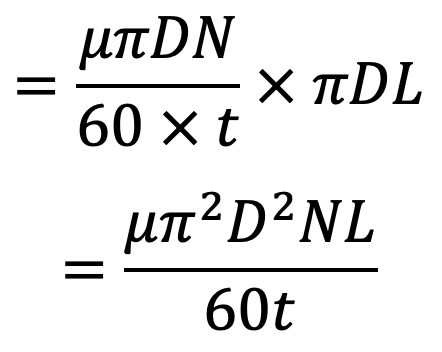
The Torque required to overcome the viscous resistance,
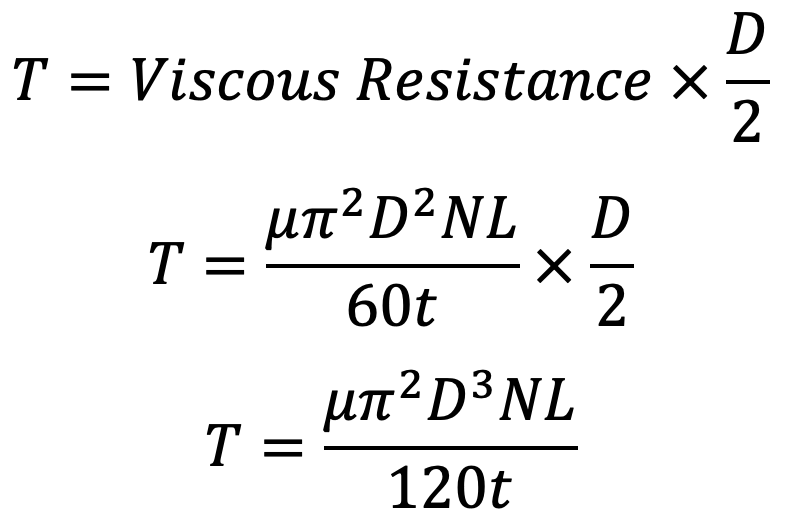
The Power absorbed in overcoming the viscous resistance will be
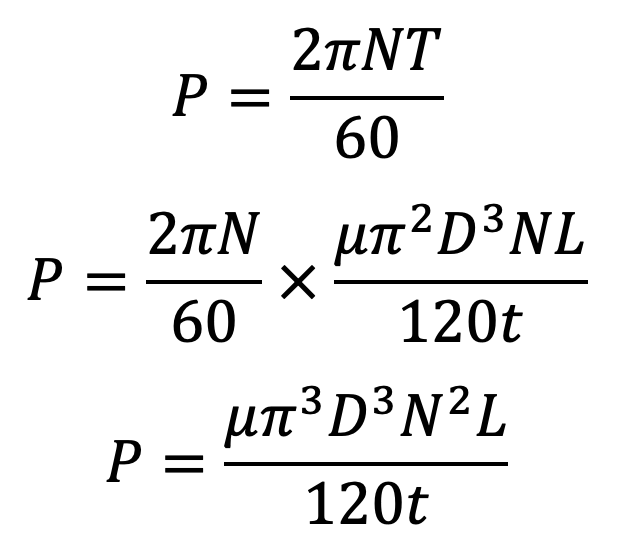
Using this formula, we can calculate the power absorbed in overcoming the viscous resistance offered by the oil.
2. Viscous Resistance of Foot-Step Bearing
In a Footstep bearing, a vertical shaft is rotating. An oil film between the bottom surface of the shaft and bearing is provided, to reduce the wear and tear. The viscous resistance is offered by the oil to the shaft. In this case, the radius of the surface of the shaft in contact with oil is not constant as in the case of the journal bearing. Hence, viscous resistance in the foot-step bearing is calculated by considering an elementary circular ring of radius r and thickness dr as shown in the following figure.
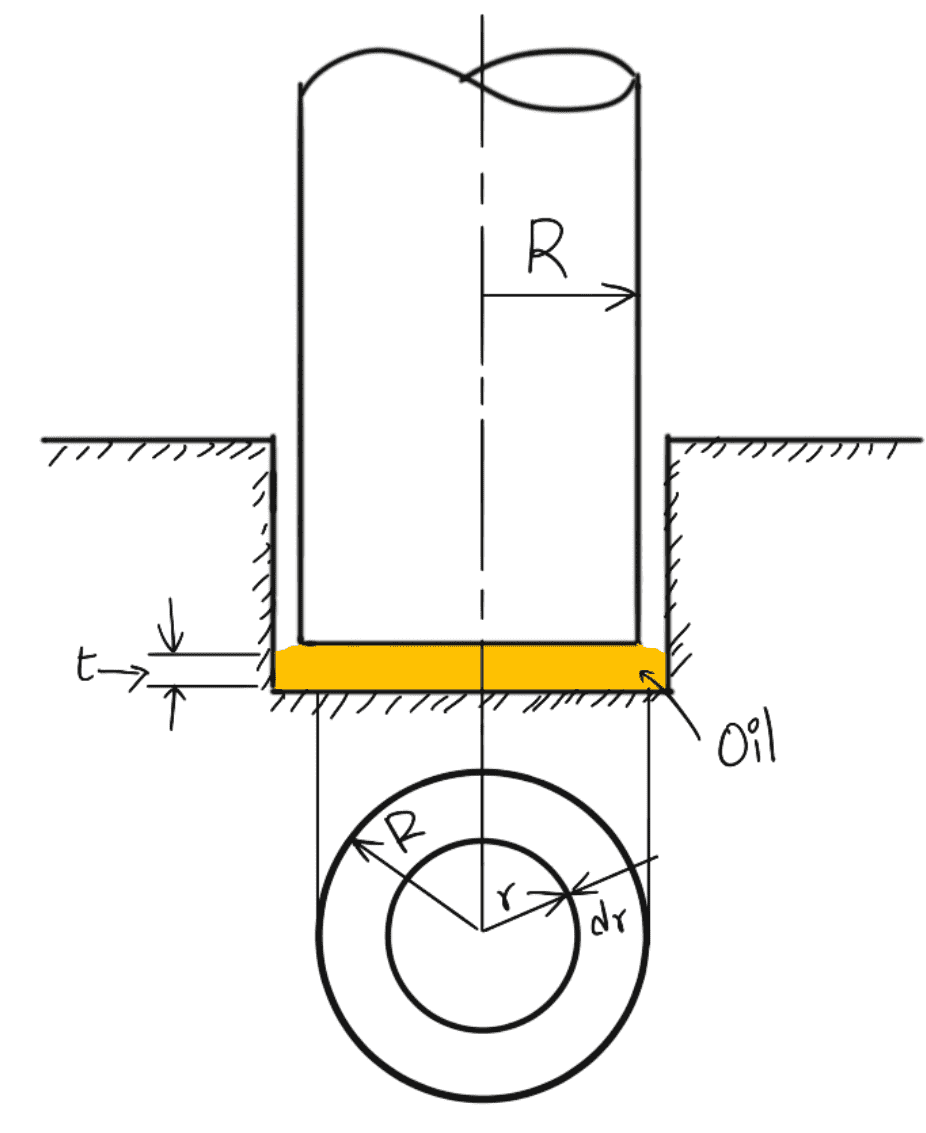
Let us say
Speed of shaft in r.p.m. = N
The thickness of oil film = t
The radius of the shaft = R
The Area of the elementary ring = 2πrdr
Now shear stress is given by as follows
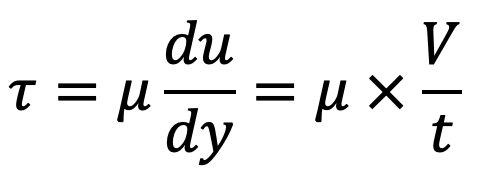
Where V is the tangential velocity of the shaft at radius r and is equal to
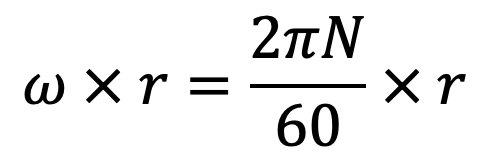
Shear force on the ring = dF = 𝜏 x area of the elementary ring
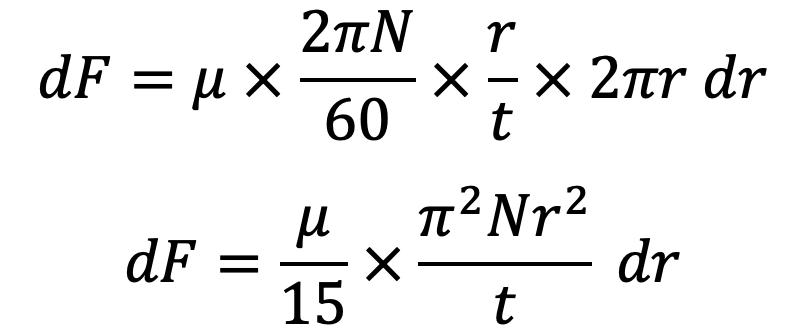
The torque is required to overcome the viscous resistance
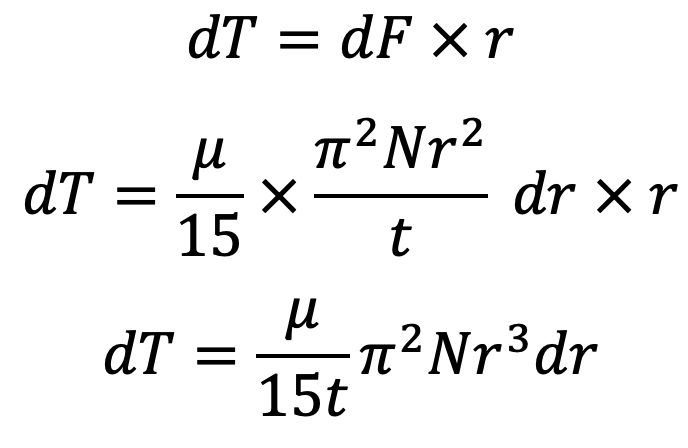
The total torque required to overcome the viscous resistance will be

Power absorbed can be written as
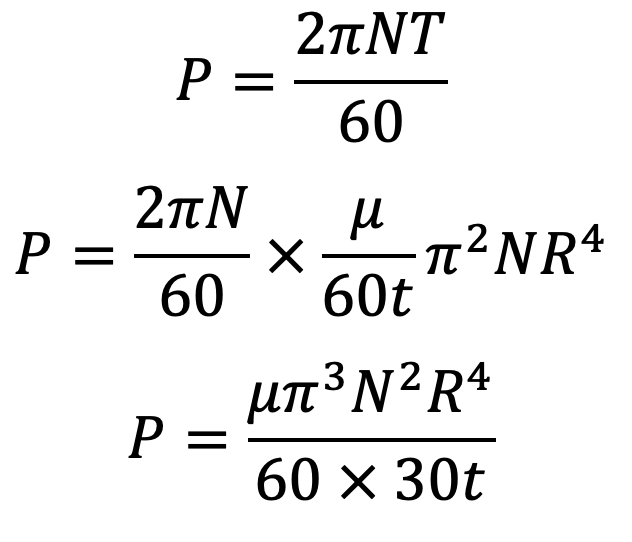
Using this formula, we can calculate the power absorbed in overcoming the viscous resistance offered by the oil.
3. Viscous Resistance of Collar Bearing
The following image shows the collar bearing, where the face of the collar is separated from the bearing surface by an oil film of uniform thickness.
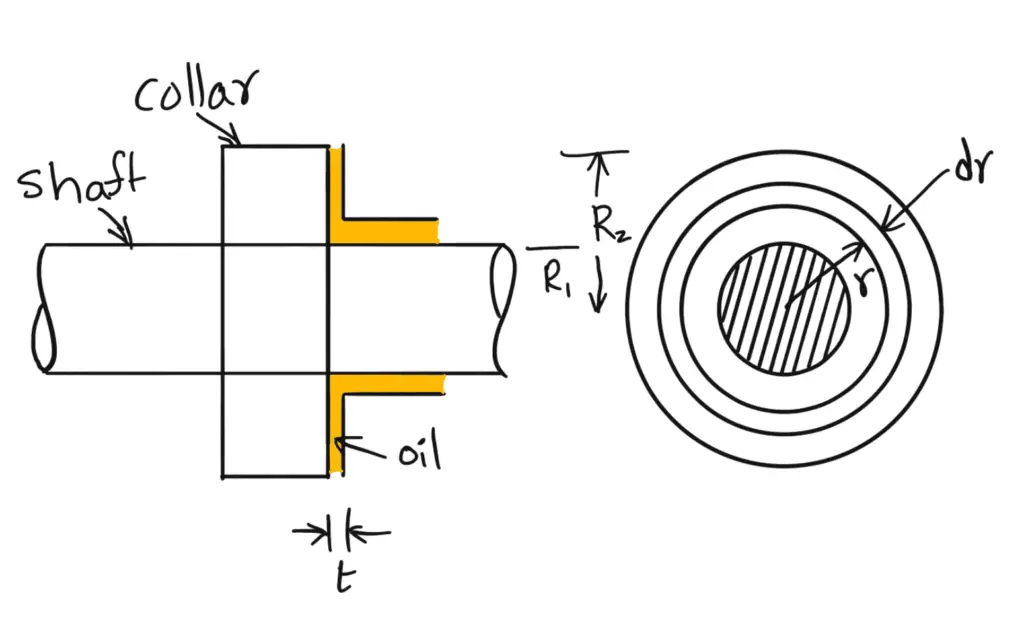
Let us say
Speed of shaft in r.p.m. = N
Internal radius of the collar = R1
The external radius of the collar =R2
Consider an elementary circular ring of radius ‘r’ and width ‘dr’ of the bearing surface.
Then the torque (dT) required to overcome the viscous resistance on the elementary circular ring is the same as given by the equation above.
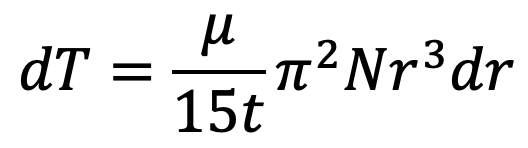
Total torque, required to overcome the viscous resistance, on the whole collar is
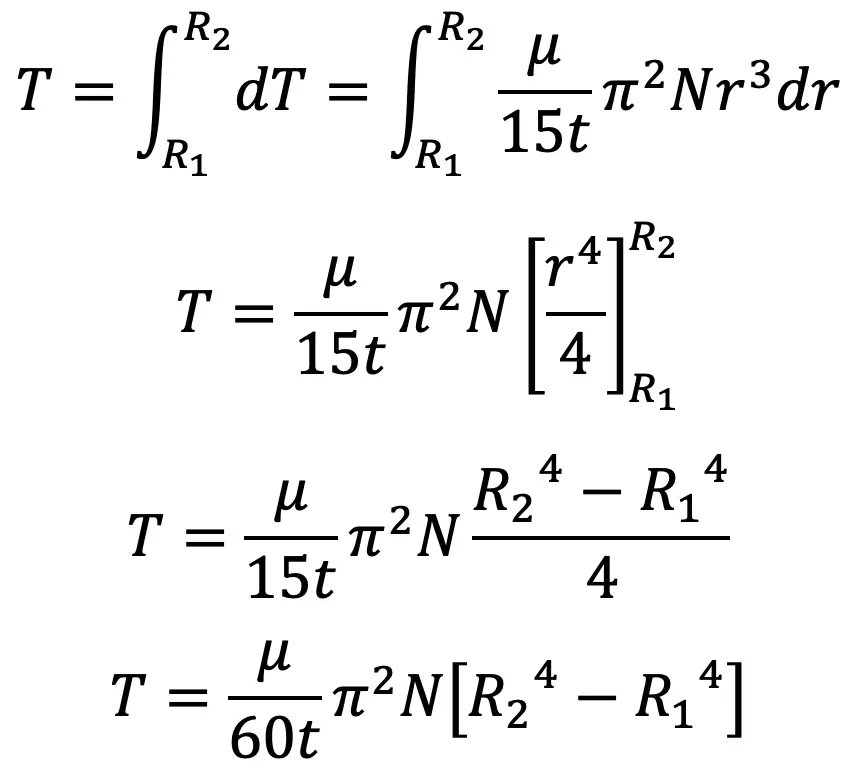
Power absorbed in overcoming viscous resistance
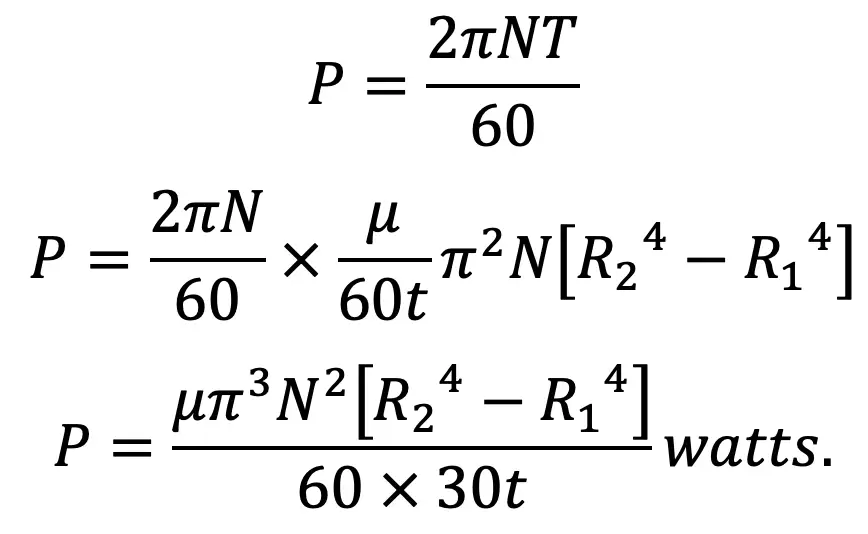
Using this formula, we can calculate the power absorbed in overcoming the viscous resistance offered by the oil.

Leave a Reply