What is Moment of Inertia formula Derivation?

 Topic: What is Moment of Inertia formula Derivation?

First of all What is Inertia?

“Inertia is a resistance force of a physical object to any change in its state of motion”

Now let’s see what is Moment of inertia? how it is different from the word “Inertia” and “Moment inertia“.

“Moment of Inertia is a resistance force of a physical object to any change in angular acceleration”

[similar topics: Force and Moment of Force, Moment of couple]

Moment of Inertia formula Derivation

The physical object is made up of small particles. The Mass Moment of Inertia of the physical object can be expressed as the sum of Products of the mass and square of its perpendicular distance from the point which is fixed (A point which causes the moment about the axis Passing thru it).

The Mass Moment of Inertia can be Denoted by I

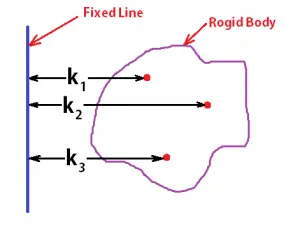
Les take a consideration of a physical Body having a mass of m. This is composed of small particles whose masses are m_1,  m_2, m_3, …… etc. respectively. The perpendicular distance of each particle from the line as shown figure are k_1,  k_2, k_3, …… etc. 

From the above statement, the Mass Moment of Inertia for the whole body can be written as

I = m₁ (k₁)² + m₂ (k₂)² + m₃ (k₃)² + …..   [eqn 1]

From the concept of the centre of mass and centre of gravity, the mass of a body assumed to be concentrated at on point.

The mass at that point is m and The perpendicular distance of the point from the fixed line is k

∴hence

m₁ (k₁)² + m₂ (k₂)² + m₃ (k₃)² + ….. = mk² …….[eqn 2]

I =mk²

where k is known as the radius of gyration.

Check this Mass moment of Inertia Calculat0r!

What is Radius of gyration?

Radius of Gyration

Radius gyration can be said as the perpendicular distance from the axis to the point at which the whole mass of the body is to be assumed to be concentrated at that point only. And also it should satisfy the eqn 2 expressed above. Then only it is said to be a radius of gyration.

Some related definitions with the mass moment of inertia are described below.

Angular Momentum

The angular moment is described as the product of the Mass Moment of Inertia and the Angular Velocity of the body.

Mathematical Expression

Angular momentum = I.ω

∴Where

I = Mass Moment of Inertia

ω = Angular Velocity of the body

Polar Moment of Inertia

Polar Moment of Inertia is a measure of resistibility of a shaft against the twisting. It is also known as the torsional Stiffness Read the Full article here

Tags: Machine Design, the moment of inertia formula derivation, inertia units, inertia formula, inertia physics, mass moment of inertia, Mechanical Engineering Basics