What is Otto Cycle?

In the previous article, we have discussed the Carnot cycle, the Stirling cycle and the Ericsson Cycle. The main disadvantage of the Carnot cycle is low mean effective pressure due to impracticable high pressure and the volume ratios. Nicolaus Otto proposed a constant volume heat addition cycle called the Otto cycle. Now we are going to discuss Otto cycle in more detail.

Otto Cycle

In 1876, Nikolaus August Otto (German Engineer) proposed this Air standard cycle. This is the idealized cycle for the spark-ignition engine.

In Spark Ignition Internal Combustion Engines, there are four operations in the thermodynamic cycles. They are,

• Suction or intake stroke,
• Compression stroke,
• Expansion or power stroke,
• Exhaust stroke

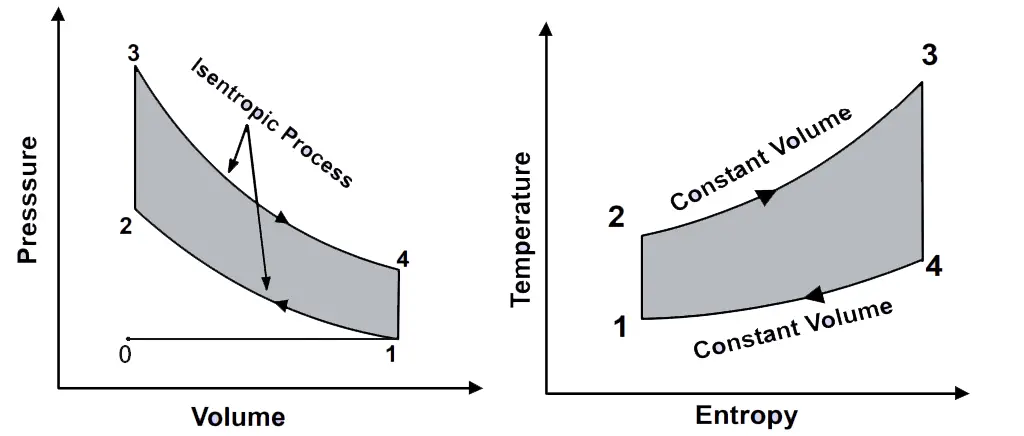
All these four processes are explained with the help of a P-V diagram and T-S diagram in the Otto Cycle.

0 → 1 and 1 → 0

When the engine is working on the full throttle, the Process 0 → 1 and 1 → 0 represents the suction and the exhaust process of Thermodynamic cycle in the P-V diagram and the effect of these two processes considered as nullified.

1 → 2

The process 1 → 2 is the isotropic compression of the air in the cylinder while piston moves from the bottom dead centre (BDC) to the top dead centre (TDC).

2 → 3

During the process, 2 → 3 the heat is supplied at a constant volume. This is the spark ignition and the combustion of the air-fuel mixture is takes place in the cylinder during this process 2 → 3.

3 → 4 & 4 → 1

These two processes 3 → 4 & 4 → 1 will represent the isotropic expansion (Piston moves from the Top dead centre to the bottom dead centre) and the constant volume heat rejection respectively.

with this the cycle completes.

Thermodynamically, the efficiency of the Otto cycle is given by

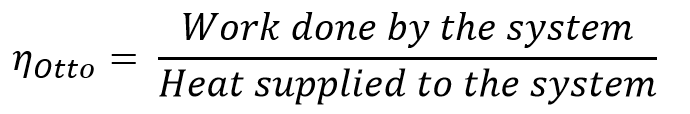
Work done by the system = Heat supplied (Q_S)- Heat rejected (Q_R)

W = Q_S – Q_R

Considering the constant volume process 2 → 3 and 4 → 1 the heat supplied and rejected of air can be written as

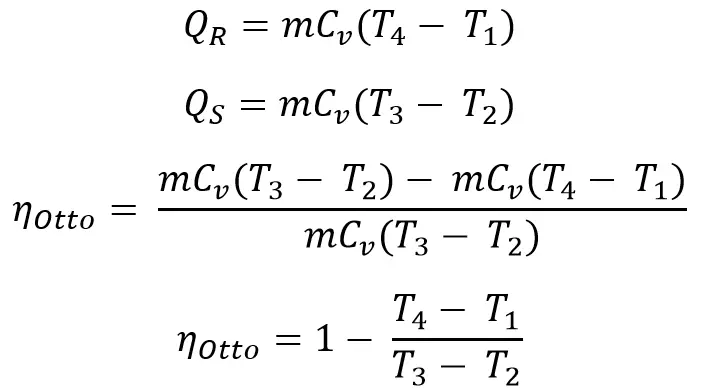
Considering the isotropic processes 1 → 2 and 3 → 4, we can write

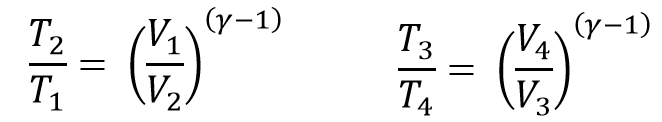
In the Otto cycle, the volume ratios are equal to the compression ratios

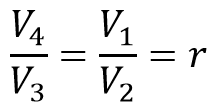
therefore

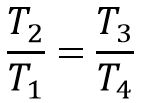
This can also be written as

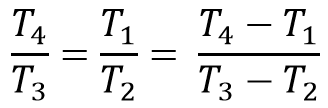
From the above thermal efficiency equation, we can write

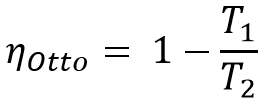
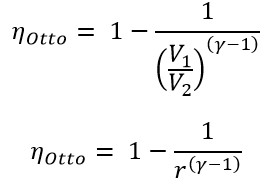
The thermal efficiency of the Otto cycle is dependent on the compression ratio r and the ratio of specific heat γ.

To increase the efficiency of the Otto cycle is possible by the increase in the compression ratio. Along with this, we can also increase the efficiency of the Otto cycle by using the working fluid with high specific heat.

The efficiency of the Otto cycle is independent of heat supplied to the system and also the pressure ratio.

Conclusion

We have discussed the different processes in the Otto cycle and the efficiency of the cycle and how we can increase the efficiency of the Otto cycle by changing certain parameters in the engine. If you have anything to say about this topic, Please let us know your thoughts in the comment section below.