Carnot cycle is a reversible Air Standard Cycle, where Internal Combustion Engines can be compared in terms of performance to judge the degree of perfection. So it is the perfect standard engine.

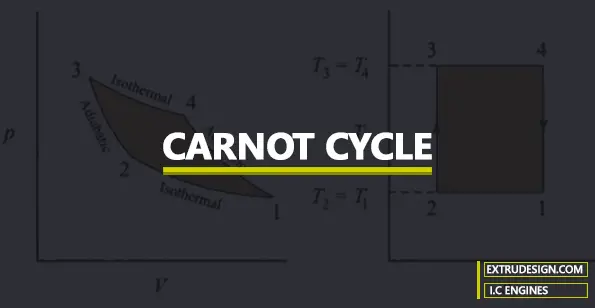
Carnot Cycle

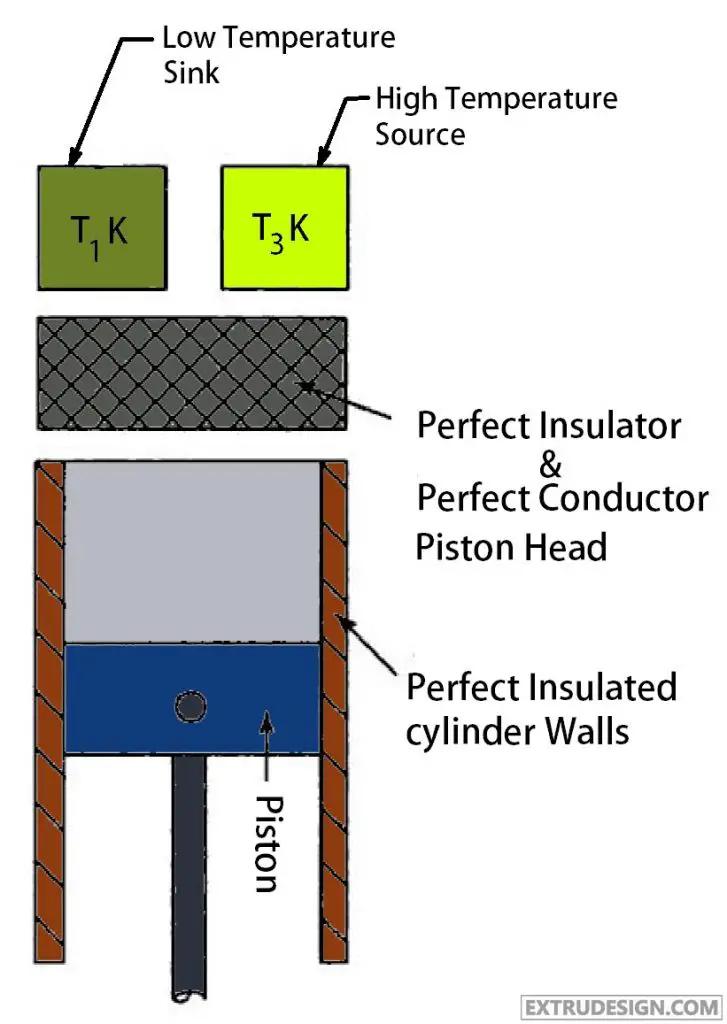
Sadi Carnot is a French engineer, who first proposed the Reversible cycle in 1824. In this cycle, the working medium receives the Heat energy from the high temperature and rejects the heat at the lower temperature.

In this Carnot Cycle there are two Isothermal processes and two Reversible Adiabatic processes. 

Carnot Engine Working Principle

The engine based on the Carnot Cycle is called the Carnot Engine. The working of the Carnot Engine is explained in this article with all the different processes involve in it.

In Internal Combustion Engines, there are four operations in the thermodynamic cycles. They are,

• Suction or intake stroke,
• Compression stroke,
• Expansion or power stroke,
• Exhaust stroke

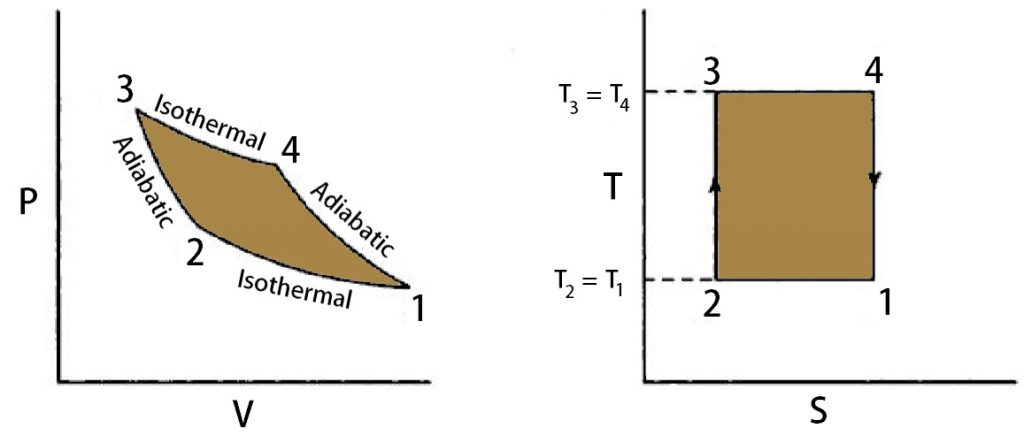
All these four processes are explained below with the help of a P-V diagram and T-S diagram in the Carnot Cycle.

3 → 4   (Isothermal Expansion)

First, the Heat is transferred from the high-temperature source (T₃) to the working medium in the cylinder. As the result, the working medium expands. this process is represented as the 3 → 4 on the below P-V diagram.

This 3 → 4 operation can be said as combustion stroke, where the Sparkplug gives the heat to the air-fuel mixture. This 3 → 4 process is an Isothermal Expansion Stroke. During this combustion stroke, the cylinder walls and the cylinder head are acts as the Perfectly insulated. Which means the valves will be closed. During this operation, there will be no change in the temperature of the system. 

You can see this from the Temperature – Entropy (T-S Diagram) diagram. From the Pressure-volume (P-V Diagram) diagram, it is observed that there will be pressure decrease in the cylinder and increase in the volume.

4 → 1 (Adiabatic Expansion)

Due to Insulated valves, the working medium will be allowed to expand further. This state is represented as 4 →1. This is an Adiabatic process. Which means there will be Thermal Energy transfer without the transfer of heat or mass. 

So there is no change in the entropy. This is observed from path 4 →1 on the T-S diagram. From the P-V diagram, there is a decrease in cylinder pressure and an increase in the cylinder volume. This stroke is called the Expansion Stroke from the thermodynamic cycle.

1 → 2 (Isothermal Compression)

Now the system will be brought into contact with the constant low-temperature sink (T₁). Which means the valves in the cylinder head will be in opened condition, which means the cylinder head will act as the Perfect Conductor. From this, the Isothermal process 1 → 2 will be started.

Some amount of heat is rejected to the sink without a change in the temperature of the sink. So this is also an Isothermal Process from the T-S diagram. In this operation, the working medium will be slightly compressed. This 1 → 2 operation is an Isothermal Compression stroke.

2 → 3 (Adiabatic Compression)

Now the valve will be closed during this compression. so there be Energy transfer without the transfer of mass. Which means adiabatic Compression. So there is no change in entropy observed from the T-S diagram, and the working medium will be highly compressed with a very slight change in the volume. from the P-V diagram.

And hence the Carnot Cycle is completed.

Thermodynamically, efficiency of the Carnot cycle is given by

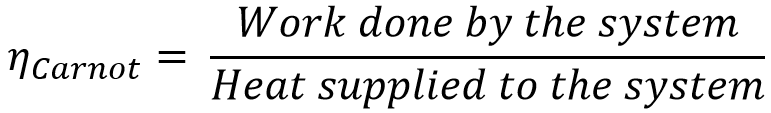
Work done by the system = Heat supplied (Q_S)- Heat rejected (Q_R)

W = Q_S – Q_R

Considering the Isothermal processes, 1 → 2 & 3 → 4, we can write

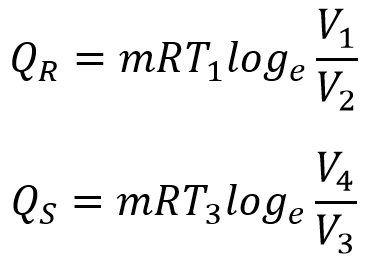
Considering the Adiabatic processes, 2 → 3 & 4 → 1, we can write

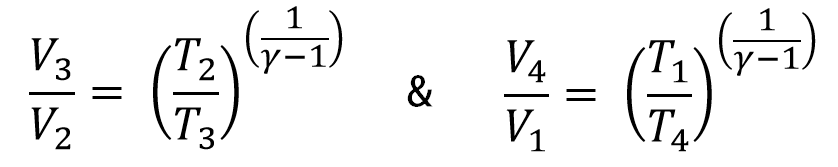
From the T-S diagram T₁ = T₂ and T₄ = T₃, we can re-write the above equation

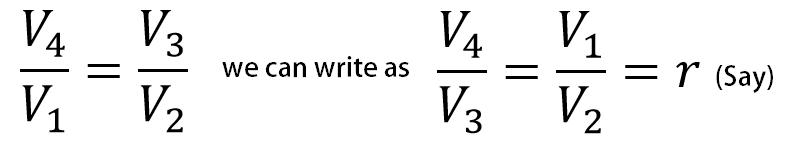
From all the above equations we can write efficiency of the cycle is,

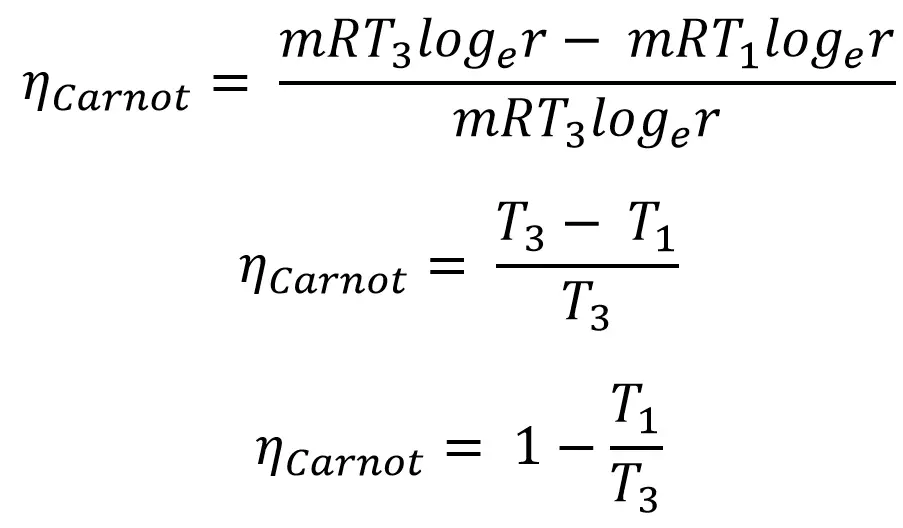
From the above equation of the efficiency of The Carnot cycle, as the sink temperature (T₁) will be the ambient or the coolant temperature. which is fixed. so to increase the efficiency of the Carnot Engine, we have to increase the Source temperature (T₃).

Conclusion

We have discussed the Carnot cycle with the P-V diagram and T-S diagram. and also we have derived the efficiency of the Carnot engine. Please let us know your thought in the comment section below.