Model Laws in Fluid Mechanics | Dimensionless Numbers

In continuation with the previous article, Model Analysis in Fluid Mechanics helps predict the performance of these hydraulic structures or hydraulic machines before actually constructing or manufacturing. Model law helps identify the dynamic similarities between the model and the prototype. Let us discuss more details on different Model Laws in Fluid Dynamics.

Dimensional Analysis and Model Analysis are two important tools to help engineers to build structures or machines which involve hydraulic fluid. Model analysis especially helps predict the performance of these hydraulic structures (such as dams, spillways etc.) or hydraulic machines (such as turbines, pumps etc.), before actually constructing or manufacturing. Models of the structures or machines are made and tests are performed on them to obtain the desired information.

What is a Model?
The model is a small-scale replica of the actual structure or machine.

What is a prototype?
The actual structure or machine is called Prototype. It is not necessary that the models should be smaller than the prototypes (though in most cases it is), they may be larger than the prototype.

The study of models of actual machines is called Model analysis. Model analysis is actually an experimental method of finding solutions to complex flow problems. Firstly, the model analysis purpose is to obtain information about the likely performance of the prototype. Secondly, to help in the design and avoid costly mistakes and evolve an economic solution to a hydraulic problem.

Before we get started with the Model laws, we need to understand the basics of Dimensionless numbers.

Dimensionless Numbers

Dimensionless numbers are those numbers which are obtained by dividing the inertia force by viscous force or gravity force or pressure force or surface tension force or elastic force. As this is a ratio of one force to the other force, it will be a dimensionless number. These dimensionless numbers are also called non-dimensional parameters.

The followings are the important dimensionless numbers:

1. Reynold’s number
2. Froude’s number
3. Euler’s number
4. Weber’s number
5. Mach’s number

1. Reynold’s Number (R_e)

It is defined as the ratio of the inertia force of a flowing fluid and the viscous force of the fluid. The expression for Reynold’s number is obtained as

Inertia force (F_i) = Mass × Acceleration of flowing fluid

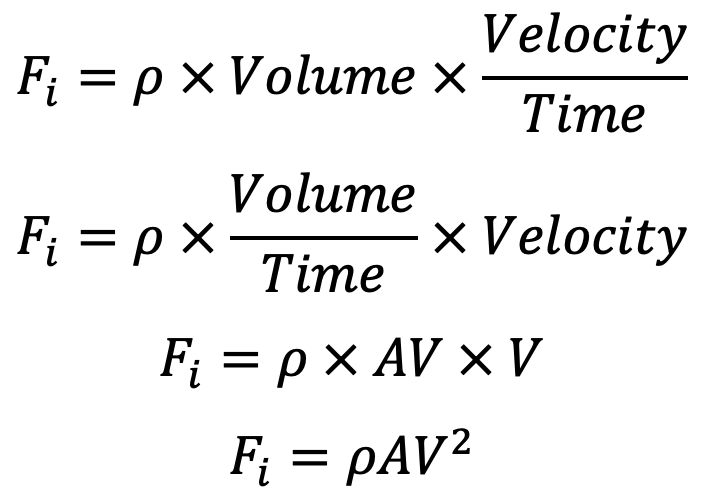
Viscous force (F_v) = Shear stress × Area

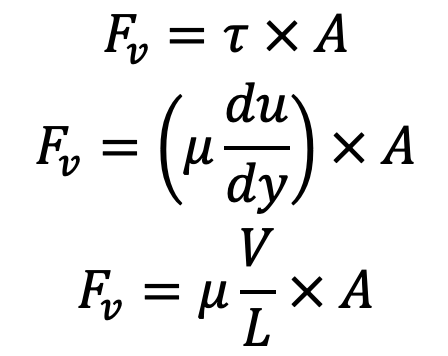
By definition, Reynold’s number,

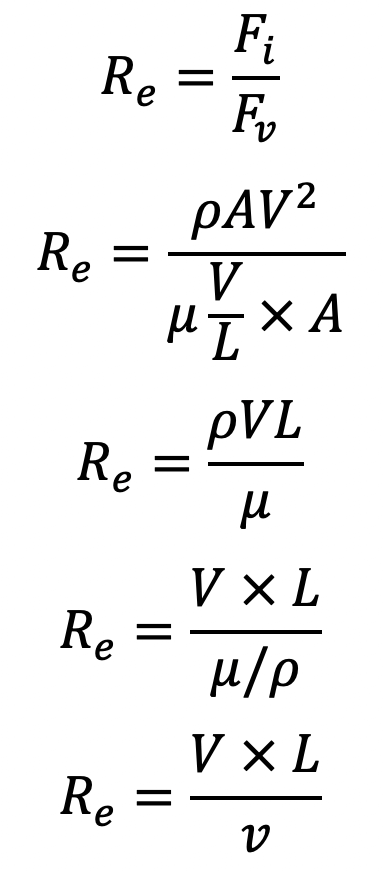
In the case of pipe flow, the linear dimension L is taken as diameter, d. Hence Reynold’s number for pipe flow,

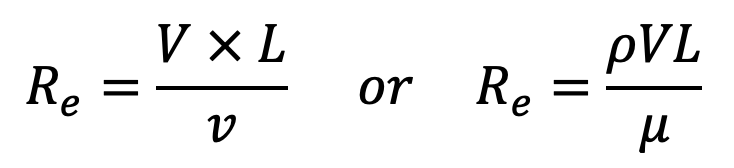
We also discussed Reynold’s experiment. Check it out here.

2. Froude’s Number (F_e)

Froude’s number is defined as the square root of the ratio of the inertia force of a flowing fluid to the gravity force. Mathematically, it is expressed as

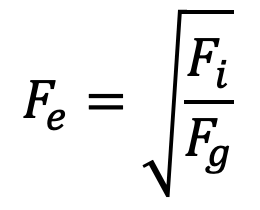
we know F_i is inertia force = ρAV²

F_g = Force due to gravity = Mass × Acceleration due to gravity = ρ × Volume × g = ρ × L³ × g
F_g = ρ × L² × L × g
F_g = ρ × A × L × g

Substituting these F_i and F_g values in the above relation we get Froude’s Number

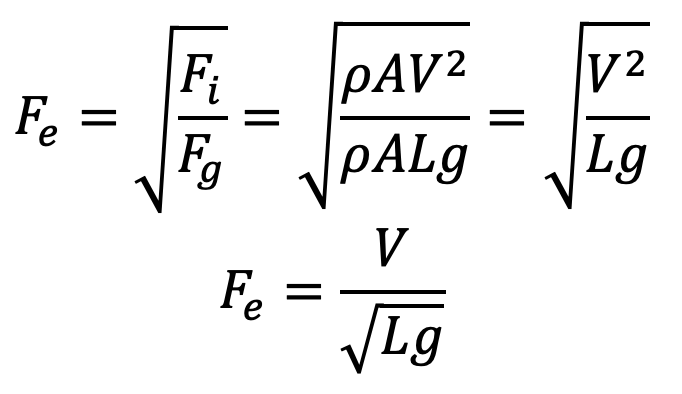
3. Euler’s Number (E_u)

It is defined as the square root of the ratio of the inertia force of a flowing fluid to the pressure force. Mathematically, it is expressed as

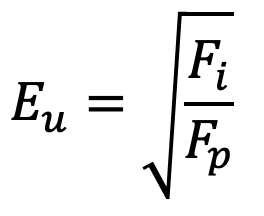
where
F_p = Intensity of pressure × Area = p x A
F_i = inertia force = ρAV²

Substituting these F_p and F_i values in the above relation we get Euler’s Number

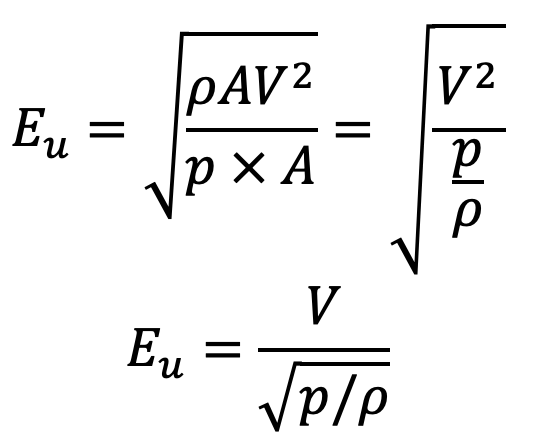
4. Weber’s Number (W_e)

It is defined as the square root of the ratio of the inertia force of a flowing fluid to the surface tension force. Mathematically, it is expressed as

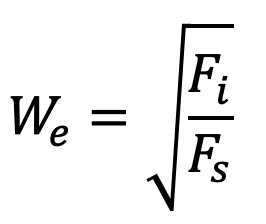
where
F_i = inertia force = ρAV²
F_s = Surface tension force = Surface tension per unit length × Length = σ × L

Substituting these F_i and F_s values in the above relation we get Weber’s Number

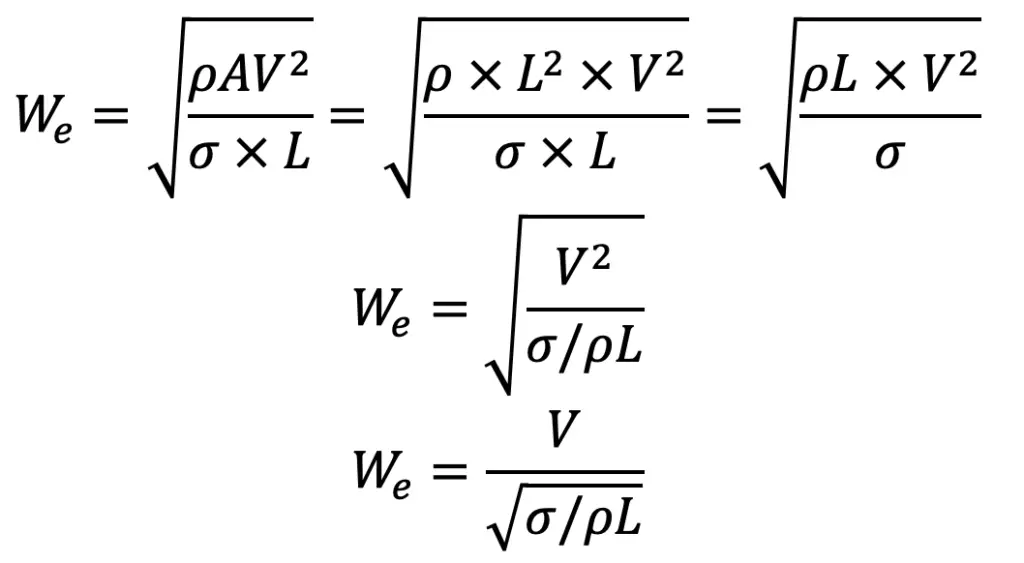
5. Mach’s Number (M)

Mach’s number is defined as the square root of the ratio of the inertia force of a flowing fluid to the elastic force. Mathematically, it is defined as

where
F_i = inertia force = ρAV²
F_e = Elastic force = Elastic stress × Area = K × A = K × L²

Substituting these F_i and F_e values in the above relation we get Weber’s Number

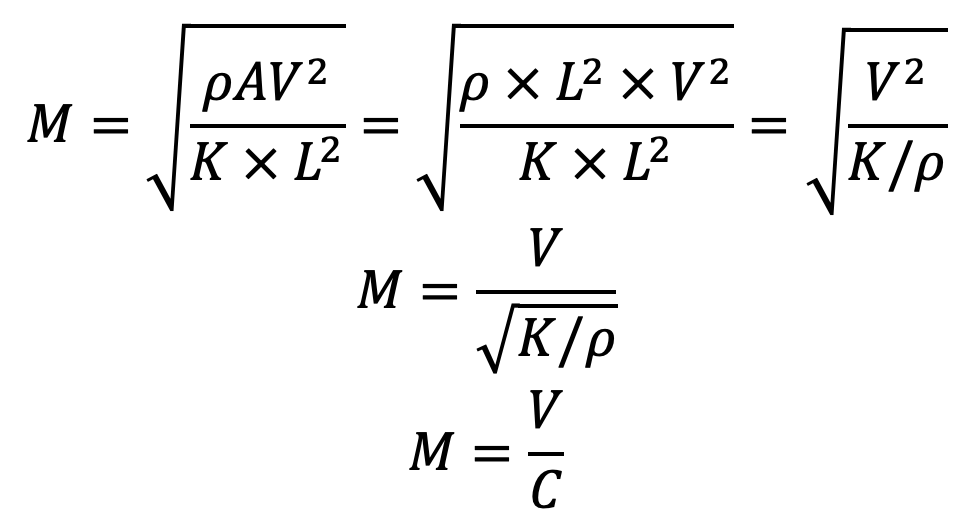
Dynamic Similarity Between Model and the Prototype

For the dynamic similarity between the model and the prototype, the ratio of the corresponding forces acting at the corresponding points in the model and prototype should be equal. The ratio of the forces is dimensionless numbers.

It means for the dynamic similarity between the model and prototype, the dimensionless numbers should be the same for the model and the prototype. But it is quite difficult to satisfy the condition that all the dimensionless numbers (i.e., R_e, F_e, W_e E_u, and M) are the same for the model and prototype.

Hence models are designed on the basis of the ratio of the force, which is dominating in the phenomenon. The laws on which the models are designed for dynamic similarity are called model laws or laws of similarity.

Model Laws or Similarity Laws

The followings are the model laws:

1. Reynold’s model law
2. Froude model law
3. Euler model law
4. Weber model law
5. Mach model law

1. Reynold’s Model Law

Reynold’s model law is the law in which models are based on Reynold’s number. Models based on Reynold’s number include:

• Pipe flow
• Resistance experienced by sub-marines, airplanes, fully immersed bodies etc.

As defined earlier the Reynold number is the ratio of inertia force and viscous force, and hence fluid flow problems where viscous forces alone are predominant, the models are designed for dynamic similarity on Reynolds law, which states that the Reynold number for the model must be equal to the Reynold number for the prototype.

Let
V_m = Velocity of fluid in the model
ρ_m = Density of fluid in the model
L_m = Length or linear dimension of the model
μ_m = Viscosity or fluid in the model
Similarly, V_p ρ_p L_p and μ_p are the corresponding values of velocity, density, linear dimension and viscosity of the fluid in the prototype. Then according to Reynold’s model law.

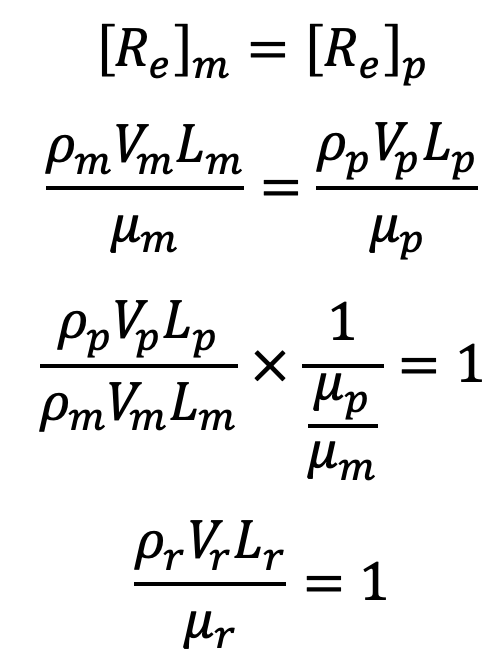
And also ρ_r, V_r, L_r, and μ_r are called the scale ratios for density, velocity, linear dimension, and viscosity.

The scale ratios for time, acceleration, force, and discharge for Reynold’s model law are obtained as

t_r = Time scale ratio = L_r / V_r

a_r = Acceleration scale ratio = V_r / t_r

F_r = Force scale ratio = (Mass × Acceleration)_r = m_r × a_r = ρ_r A_r V_r × a_r = ρ_r L_r² V_r × a_r

Q_r = Discharge scale ratio = (ρAV)_r = ρ_r A_r V_r = ρ_r L_r² V_r

2. Froude Model Law

Froude model law is the law in which the models are based on the Froude number which means for the dynamic similarity between the model and prototype, the Froude number for both of them should be equal. The Froude model law is applicable when the gravity force is only the predominant force which controls the flow in addition to the force of inertia. The Froude model law is applied in the following fluid flow problems:

1. Free surface flows such as flow over spillways, weirs, sluices, channels etc.
2. The flow of jet from an orifice or nozzle
3. Where waves are likely to be formed on the surface,
4. Where fluids of different densities flow over one another

Let
V_m = Velocity of fluid in the model
L_m = Linear dimension or length of model
g_m = Acceleration due to gravity at a place where the model is tested.
Similarly, V_p, L_p and g_p are the corresponding values of the velocity, length and acceleration due to gravity for the prototype. Then according to the Froude model law,

(F_e)_Model = (F_e)_Prototype

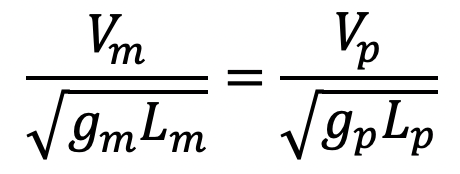
If the tests on the model are performed in the same place where the prototype is to operate, then g_m = g_p and the above equation becomes as

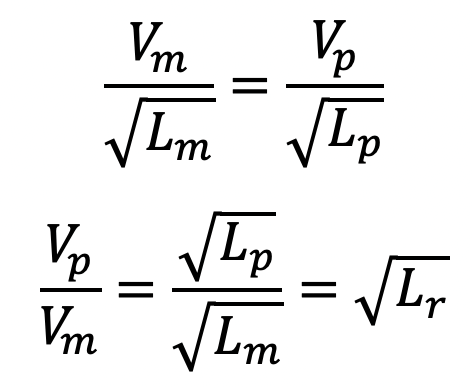
where
L_r = Scale ratio for length
V_p / V_m = V_r = Scale ratio for velocity

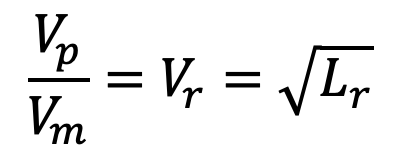
3. Euler’s Model Law

Euler’s model law is the law in which the models are designed on Euler’s number (E_u) which means for the dynamic similarity between the model and prototype, the Euler number for model and prototype should be equal. Euler’s model law is applicable when the pressure forces are alone predominant in addition to the inertia force.

According to this law

(E_u)_model = (E_u)_prototype

We know, Euler’s number

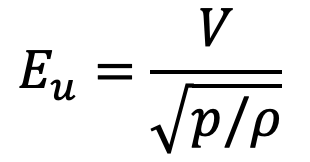
If
V_m = Velocity of fluid in the model,
P_m = Pressure of fluid in the model,
ρ_m = Density of fluid in the model,
Similarly, V_p, P_m, ρ_m = Corresponding values in the prototype

Substituting these values in equation (E_u)_model = (E_u)_prototype, we get

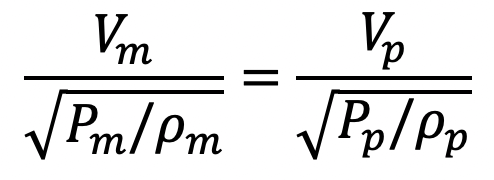
If the fluid is the same in model and prototype, then the above equation becomes as follows

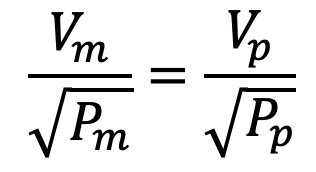
Euler’s model law is applied for fluid flow problems where flow is taking place in a closed pipe in
which case turbulence is fully developed so that viscous forces are negligible and gravity force and
surface tension force is absent. This law is also used where the phenomenon of cavitation takes place.

4. Weber Model Law

Weber model law is the law in which models are based on Weber’s number, which is the ratio of the square root of inertia force to surface tension force. Hence where surface tension effects predominate in addition to inertia force, the dynamic similarity between the model and prototype is obtained by equating the Weber number(W_e) of the model and its prototype.

Hence according to this law

(W_e)_model = (W_e)_prototype

Weber number is

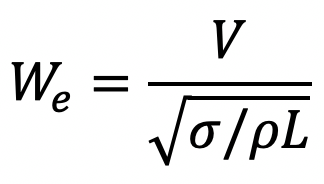
V_m = Velocity of fluid in model,
σ_m = Surface tensile force in model,
ρ_m = Density of fluid in model,
L_m = Length of surface in model,
Similarly, V_p, σ_p, ρ_p, L_p = Corresponding values of fluid in prototype

Then according to Weber law, we have

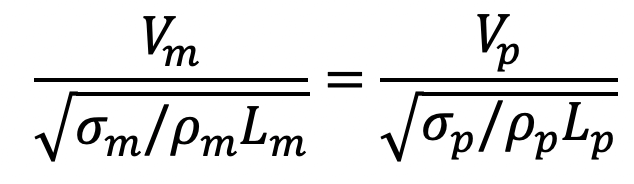
Weber model laws applied in the following cases:

1. The capillary rise in narrow passages
2. Capillary movement of water in the soil
3. Capillary waves in channels
4. Flow over weirs for small heads

5. Mach Model Law

Mach model law is the law in which models are designed on Mach number, which is the ratio of the square root of inertia force to the elastic force of a fluid. Hence where the forces due to elastic compression predominate in addition to inertia force, the dynamic similarity between the model and its prototype is obtained by equating the Mach number of the model and its prototype.

Hence according to this law:

(M)_model = (M)_prototype

We know the Mach number is

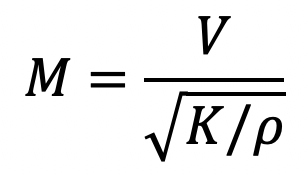
V_m = Velocity of fluid in model
K_m = Elastic stress for model
ρ_m = Density of fluid in model
Similarly, V_p, K_p and ρ_p = Corresponding values for the prototype.

Then according to Mach’s law,

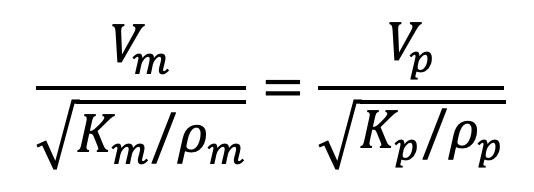
Mach model law is applied in the following cases:

1. The flow of aeroplane and projectile through the air at supersonic speed, i.e., at a velocity more than the velocity of sound
2. Aerodynamic testing
3. Underwater testing of torpedoes
4. Water-hammer problems.

These are the 5 model laws that help us determine the dynamic similarity between the model and the prototype, and the ratio of the corresponding forces acting at the corresponding points in the model and prototype. Let us know what you know about this article about Model Laws in the comment section below.