Model Analysis in Fluid Dynamics

In Fluid Mechanics, Dimensional Analysis and Model Analysis are two important tools to help engineers to build structures or machines which involve hydraulic fluid. Model analysis especially helps predict the performance of these hydraulic structures (such as dams, spillways etc.) or hydraulic machines (such as turbines, pumps etc.), before actually constructing or manufacturing. In the previous article, we already discussed the different Methods of Dimensional Analysis, in this article let us discuss more details on Model Analysis in Fluid Dynamics.

Model Analysis

As we mentioned above the Model Analysis in Fluid Dynamics helps predict the performance of these hydraulic structures (such as dams, spillways etc.) or hydraulic machines (such as turbines, pumps etc.), before actually constructing or manufacturing. Models of the structures or machines are made and tests are performed on them to obtain the desired information.

What is a Model?
The model is a small-scale replica of the actual structure or machine.

What is a prototype?
The actual structure or machine is called Prototype. It is not necessary that the models should be smaller than the prototypes (though in most cases it is), they may be larger than the prototype.

The study of models of actual machines is called Model analysis. Model analysis is actually an experimental method of finding solutions to complex flow problems. Firstly, the model analysis purpose is to obtain information about the likely performance of the prototype. Secondly, to help in the design and avoid costly mistakes and evolve an economic solution to a hydraulic problem.

Application of Model Analysis

Following are the applications and the challenges where we use this model analysis to solve the model problems by conducting the model investigations.

• Dams: The design of every major dam is checked by model tests before its construction. Besides the model of the dam, all its connected works like spillways, penstocks and gates are studied in order to get detailed information on the flow of water and its effect on the structure.
• Rivers and Channels: The dredging of rivers and straightening of channels, protection of banks and bottoms from erosion, and various forms of river control and improvement.
• Harbours: the wave action of harbours is concerned mainly with the effectiveness of the proposed breakwaters for providing protection from waves, and the extent of damage the waves may inflict on the breakwaters.
• Hydraulic Machines: Small-scale model tests are useful for obtaining performance data for hydraulic turbines and other turbo machines and centrifugal pumps. The model study is a very valuable guide to designers of turbo machines.
• Structures: Where prototype testing is difficult or costly, models provide the proper solution. Many structural tests like deflection tests and destructive and non-destructive testing of structures can be satisfactorily performed on models. Photoelastic and analogy methods of testing models of dams are very common.
• Ships: Towing models in a canal are helpful in estimating Drag force and wave patterns of naval vessels.
• Seepage Problems: It is possible to make studies of seepage flow on geometrically similar sectional models in glass flumes, to find out the uplift pressures on hydraulic structures.

Advantages of the Dimensional Analysis and Model Analysis

Exact analytical solutions are possible only for a limited number of flow problems. The followings are the advantages of the Dimensional Analysis and Model Analysis:

1. The performance of the hydraulic structure or hydraulic machine can be easily predicted, in advance, from its model.
2. With the help of dimensional analysis, a relationship between the variables influencing a flow problem in terms of dimensionless parameters is obtained. This relationship helps in conducting tests on the model.
3. The merits of alternative designs can be predicted with the help of model testing. The most economical and safe design may be, finally, adopted.
4. The tests performed on the models can be utilized for obtaining, in advance, useful information about the performance of the prototypes b only if a complete similarity exists between the model and the prototype.

Similitude (Types of Similarities)

Similitude is defined as the similarity between the model and its prototype in every respect, which means that the model and prototype have similar properties or model and prototype are completely similar. Three types of similarities must exist between the model and prototype. They are

1. Geometric Similarity
2. Kinematic Similarity
3. Dynamic Similarity

1. Geometric Similarity

The geometric similarity is said to exist between the model and the prototype. The ratio of all corresponding linear dimensions in the model and prototype is equal.

Let
L_m = Length of the model
b_m = Breadth of model
D_m = Diameter of model
A_m = Area of model
V_m = Volume of model

Similarly, L_p, b_p, D_p, A_p, V_p = Corresponding values of the prototype.

For geometric similarity between model and prototype, we must have the relation,

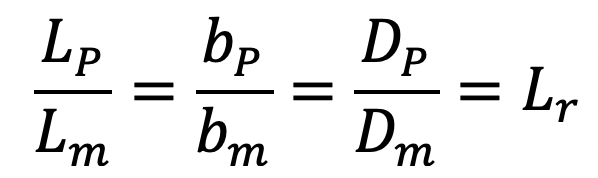
where L_r is called the scale ratio.

For area’s ratio and volume ratio the relation should be as given below:

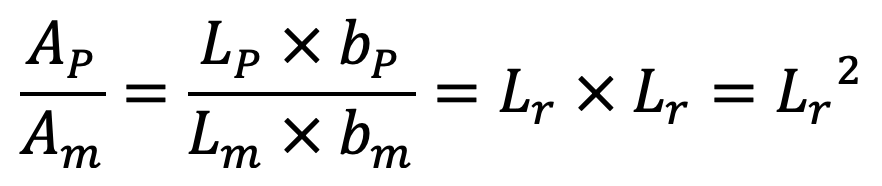
and

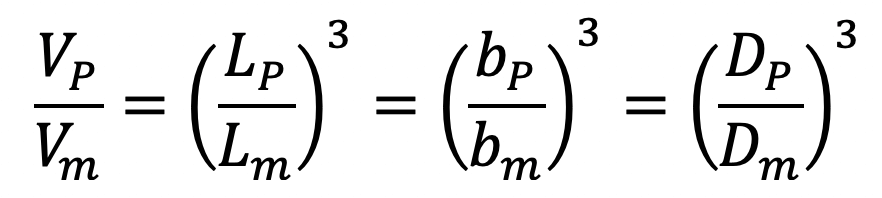
2. Kinematic Similarity

Kinematic similarity means the similarity of motion between the model and prototype. Thus kinematic similarity is said to exist between the model and the prototype if the ratios of the velocity and acceleration at the corresponding points in the model and at the corresponding points in the prototype are the same. Since velocity and acceleration are vector quantities, hence not only the ratio of the magnitude of velocity and acceleration at the corresponding points in the model and prototype should be the same, but the directions of velocity and acceleration at the corresponding points in the model and prototype also should be parallel.

Let
V_P1 = Velocity of fluid at point 1 in prototype
U_P2 = Velocity of fluid at point 2 in prototype
a_P1 = Acceleration of fluid at point 1 in prototype
a_P2 = Acceleration of fluid at point 2 in prototype

Similarly V_m1, V_m2, a_m1, a_m2 = Corresponding values at the corresponding points of fluid velocity and acceleration in the model.

For kinematic similarity, we must have

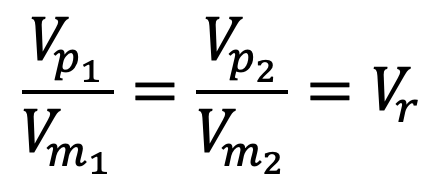
where V_r is the velocity ratio

For acceleration, we must have

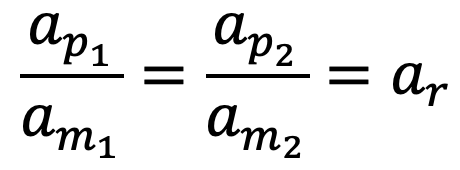
where a_r is the acceleration ratio.

Also, the directions of the velocities in the model and prototype should be the same.

3. Dynamic Similarity

Dynamic similarity means the similarity of forces between the model and prototype. Thus dynamic similarity is said to exist between the model and the prototype if the ratios of the corresponding forces acting at the corresponding points are equal. Also, the directions of the corresponding forces at the corresponding points should be the same.

Let
(F_i)_p = Inertia force at a point in prototype,
(F_v)_p = Viscous force at the point in the prototype
(Fg)p = Gravity force at the point in the prototype

Similarly, (F_i)_m (F_v)_m (F_g)_m = Corresponding values of forces at the corresponding point in the model.

Then for dynamic similarity, we have

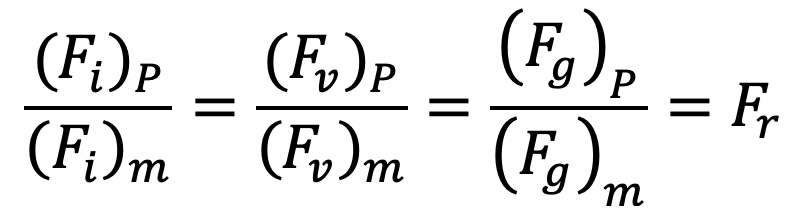
Also the directions of the corresponding forces at the corresponding points in the model and prototype should be the same.

Forces Acting In Moving Fluid

1. Inertia Force (F_i): It is equal to the product of mass and acceleration of the flowing fluid and acts in the direction opposite to the direction of acceleration. It is always existing in the fluid flow problems.
2. Viscous Force (F_v): It is equal to the product of shear stress (t) due to viscosity and surface area of the flow. It is present in fluid flow problems where viscosity is having an important role to play.
3. Gravity Force (F_g): It is equal to the product of mass and acceleration due to the gravity of the flowing fluid. It is present in the case of open surface flow.
4. Pressure Force (Fp): It is equal to the product of pressure intensity and cross-sectional area of the flowing fluid. It is present in the case of pipe flow.
5. Surface Tension Force (Fs): It is equal to the product of surface tension and the length of the surface of the flowing fluid.
6. Elastic Force (Fe): It is equal to the product of elastic stress and the area of the flowing fluid. For a flowing fluid, the above-mentioned forces may not always be present. And also the forces, which are present in a fluid flow problem, are not of equal magnitude. There are always one or two forces which dominate the other forces. These dominating forces govern the flow of fluid.

Dynamic Similarity Between Model and the Prototype

For the dynamic similarity between the model and the prototype, the ratio of the corresponding forces acting at the corresponding points in the model and prototype should be equal. The ratio of the forces is dimensionless numbers.

It means for the dynamic similarity between the model and prototype, the dimensionless numbers should be the same for the model and the prototype. But it is quite difficult to satisfy the condition that all the dimensionless numbers (i.e., R_e, F_e, W_e E_u, and M) are the same for the model and prototype.

Hence models are designed on the basis of the ratio of the force, which is dominating in the phenomenon. The laws on which the models are designed for dynamic similarity are called model laws or laws of similarity.

Model Laws

The followings are the model laws

1. Reynold’s model law
2. Froude model law
3. Euler model law
4. Weber model law
5. Mach model law

Let us discuss these in the detailed article.

Let us know what you think about this article in the comment section. Also, let us know if I need to discuss these laws in this same article. Let me know your thoughts on this.