What are the Methods Of Dimensional Analysis?

Dimensional analysis is a method of dimensions. It is a mathematical technique used in research work for design and for conducting model tests. There are two different methods of Dimensional analysis. The first one is Rayleigh’s method and Buckingham’s π-theorem. In this article, let us discuss more details on these methods of Dimensional Analysis.

Dimensional Analysis

As we have already mentioned Dimensional Analysis is a mathematical technique used in research work for design and for conducting model tests. The dimensional analysis deals with the dimensions of the physical quantities involved in the phenomenon. All physical quantities are measured by comparison, which is made with respect to an arbitrarily fixed value. Length L, mass M and time T are three fixed dimensions which are of importance in Fluid Mechanics.

If in any problem of fluid mechanics, heat is involved then the temperature is also taken as a fixed dimension. These fixed dimensions are called fundamental dimensions or fundamental quantities.

Dimension Quantities

There are basically 3 fundamental quantities. These are Length (L), Mass (M), and Time (T). Further, we have the geometric Quantities Area (A) and Volume (V).

From these fundamental quantities, we can derive secondary quantities. Secondary or derived quantities are those quantities which possess more than one fundamental dimension. For example, velocity is denoted by distance per unit of time (L/T), density is mass per unit volume (M/L³) and acceleration is distance per second square (L/T²). The Secondary or derived quantities are all of the Kinematic and Dynamic Quantities.

Let us derive a few of these Kinematic and Dynamic Quantities.

(i) Angular Velocity

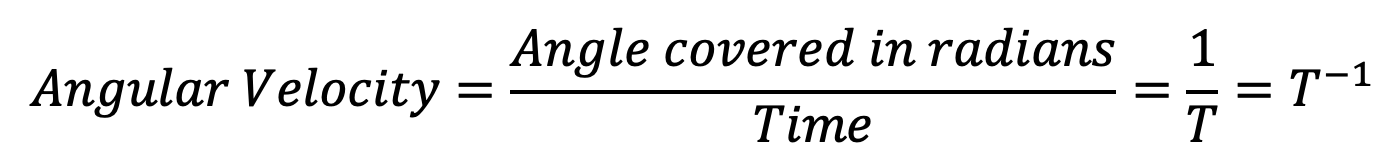
(ii) Angular Acceleration

= rad / sec²
= rad / T²
= 1 / T²
= T^-2

(iii) Discharge

Discharge = Area × Velocity
= L² × (L/T)
= L³ T^-1

(iv) Kinematic Viscosity

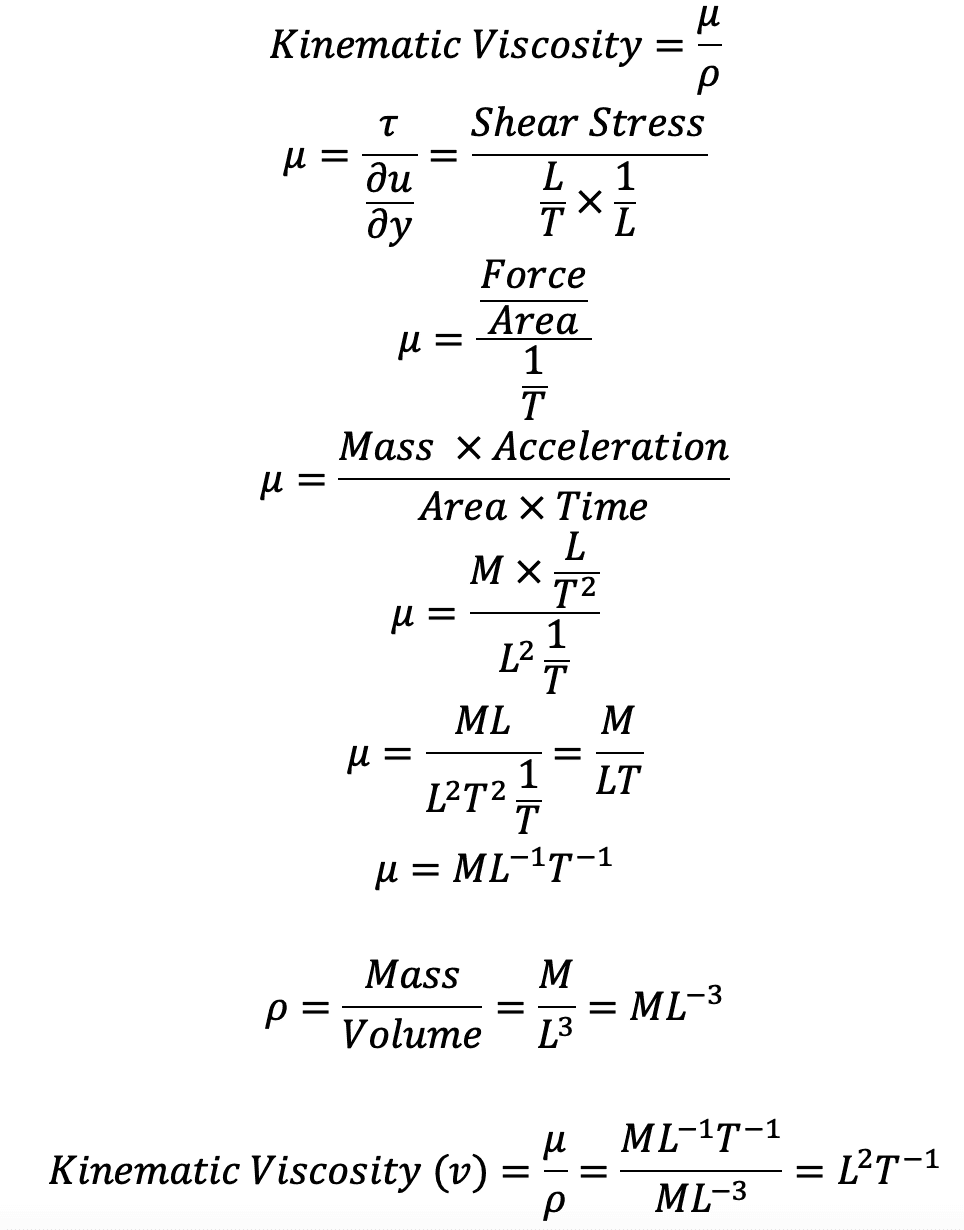
(v) Force

Force = Mass × Acceleration = M × (L/T²) = MLT^-2

(vi) Specific Weight

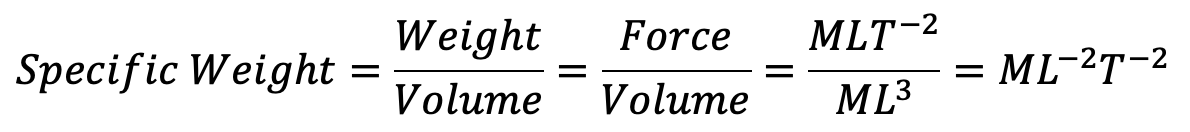
(vi) Dynamic Viscosity

Dynamic Viscosity μ is already derived above in the Kinematic viscosity derivation from the above

μ = ML^-1T^-1

Methods Of Dimensional Analysis

If the number of variables involved in a physical phenomenon is known, then the relationship among the variables can be determined by the following two methods :

1. Rayleigh’s method
2. Buckingham’s π-theorem

1. Rayleigh’s Method

This method is used for determining the expression for a variable which depends upon a maximum of three or four variables only. If the number of independent variables becomes more than four, then it is very difficult to find the expression for the dependent variable.

Let X is a variable, which depends on X₁, X₂ and X₃ variables. Then according to Rayleigh’s method, X is the function of X₁, X₂, and X₃, and mathematically it is written as X = f [X₁, X₂, X₃].

This can also be written as X = KX₁^a . X₂^b . X₃^c

Where K is constant and a, b and c are arbitrary powers.

The values of a, b and c are obtained by comparing the powers of the fundamental dimension on both sides. Thus the expression is obtained for the dependent variable.

Expression for a Time Period of Pendulum

We need to derive an expression for the time period (t) of a pendulum depends upon the length (L) of the pendulum and acceleration due to gravity (g).

Time period t is a function of (i) L and (ii) g

t = KL^a. g^b, where K is a constant

Substituting the dimensions on both sides T¹ = KL^a. (LT^-2)^b
Equating the powers of M, L and T on both sides, we have

Power of T

1 = -2b
b = -1/2

Power of L

0 = a + b
a = -b
a = -(-1/2)
a = 1/2

Substituting the values of a and b in the above equation, we get

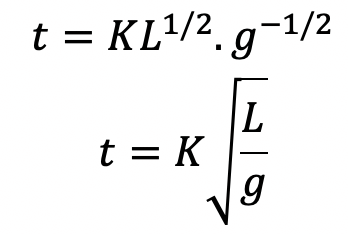
The value of K is determined from experiments which are given as

K = 2π

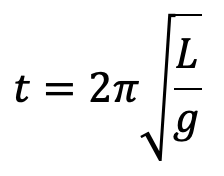
Solving Problems by Rayleigh’s Method

Problem Statement: The resisting force R of a supersonic plane during flight can be considered as dependent upon the length of the aircraft I, velocity V, air viscosity μ, air density ρ and bulk modulus of air K. Express the functional relationship between these variables and the resisting force.

Answer:

The resistance force depends on the following dimensions

Length, l
velocity, V
viscosity, M
density, ρ
Bulk modulus, K

R = Al^a . V^b . μ^c . ρ^d . K^e

where A is the non-dimensional constant.
Substituting the dimensions on both sides of the above equation,

MLT^-2 = AL^a . (LT^-1)^b . (ML^-1T^-1)^c . (ML^-3)^d . (ML^-1T^-2)^e

Equating the powers of M, L, T on both sides,

Power of M, 1 = c + d + e
Power of L, 1 = a + b – c – 3d – e
Power of T, -2 = – b – c – 2e

There are five unknowns but equations are only three. Expressing the three unknowns in terms of
two unknowns (μ and K).

Express the values of a, b and d in terms of c and e.

Solving,
d = 1 – c – e
b = 2 – c – 2e
a = 1 – b + c + 3d + e
= 1 – (2-c – 2e) + c + 3 (1 – c – e) +e
= 1 – 2 + c + 2e + c + 3 – 3c – 3e + e
a = 2 – c

Substituting these values in resisting force equation, we get

R = Al^a . V^b . μ^c . ρ^d . K^e
R = Al^2-c . V^2-c-2e . μ^c . ρ^1-c-e . K^e
R = A l² V² . ρ(l^-c V^-c μ^c ρ^-c) . V^-2e ρ^-e K^e

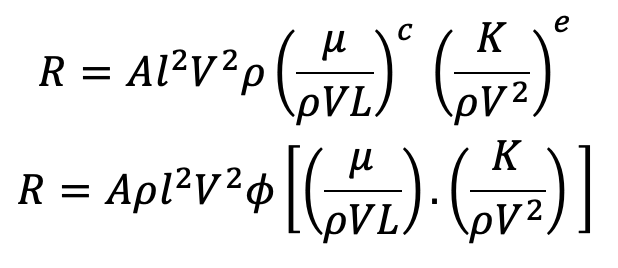
2. Buckingham’s π-Theorem

Rayleigh’s method of dimensional analysis becomes more laborious if the variables are more than the number of fundamental dimensions (M, L, T). This difficulty is overcome by using Buckingham’s π-theorem.

Buckingham’s π-Theorem states, “If there are n variables (independent and dependent variables) in a physical phenomenon and if these variables contain m fundamental dimensions (M, L, T), then the variables are arranged into (n – m) dimensionless terms. Each term is called π-term”.

Let X₁, X₂, X₃, …. X_n are the variables involved in a physical problem. Let X₁, be the dependent variable and X₂, X₃, …. X_n, are the independent variables on which X₁, depends. Then X₁, is a function of X₂, X₃, …. X_n, and mathematically it is expressed as

X₁ = f(X₂, X₃, …. X_n)

… Equation (a)

Equation (a) can also be written as

f(X₁, X₂, X₃, …. X_n) = 0

… Equation (b)

Equation (b) is a dimensionally homogeneous equation. It contains n variables. If there are m fundamental dimensions then according to Buckingham’s π-theorem, equation (b) can be written in terms of a number of dimensionless groups or -terms in which the number of π-terms is equal to (n-m). Hence equation (b) becomes as

f(π₁, π₂, π₃, …. π_n-m) = 0

… Equation (c)

Each of the π-terms is dimensionless and is independent of the system. Division or multiplication by a constant does not change the character of the π-term. Each π-term contains m + 1 variables, where m is the number of fundamental dimensions and is also called repeating variables.

Let in the above case X₂, X₃, and X₄ are repeating variables if the fundamental dimension m (M, L, T) = 3

Then each π-term is written as

π₁ = X₂^a₁ . X₃^b₁ . X₄^c₁ . X₁
π₂ = X₂^a₂ . X₃^b₂ . X₄^c₂ . X₅
:
:
π_n-m = X₂^a_n-m . X₃^b_n-m . X₄^c_n-m . X_n

….. Equation (d)

Each equation is solved by the principle of dimensional homogeneity and values of a₁, b₁, c₁, etc., are obtained. These values are substituted in equation (d) and values of π₁, π₂, ….π_n-m are obtained. These values of π’s are substituted in equation (c). The final equation for the phenomenon is obtained by expressing any one of the π-terms as a function of others as

π₁ = φ[π₁, π₂, π₃, …. π_n-m]
π₂ = φ₁[π₁, π₂, π₃, …. π_n-m]

….. Equation (e)

Procedure for Solving Problems by Buckingham’s π-theorem

The procedure for solving problems by Buckingham’s -theorem is explained by considering a problem statement which is also solved by Rayleigh’s method above.

Problem Statement: The resisting force R of a supersonic plane during flight can be considered as dependent upon the length of the aircraft I, velocity V, air viscosity μ, air density ρ and bulk modulus of air K. Express the functional relationship between these variables and the resisting force.

Answer:

Step 1:

The resistance force depends on the following dimensions

Length, l
velocity, V
viscosity, M
density, ρ
Bulk modulus, K

Hence R is a function of I, V, μ, ρ and K. Mathematically,

R = f(l, V, μ, ρ, K)

or it can be written as f₁ (R, I, V, μ, ρ, K) = 0

Total number of variables, n = 6.
Number of fundamental dimensions, m = 3.
m is obtained by writing dimensions of each variables as

R = MLT^-2 V = LT^-1, μ = ML^-1T^-1, ρ = ML^-3, K = ML^-1T^-2

Thus as fundamental dimensions in the problem are M, L, T and hence m= 3

Number of dimensionless π-terms = n – m = 6 – 3 = 3.

Thus three π-terms say π₁, π₂, and π₃, are formed. Hence we can write the above equation as

f(π₁, π₂, π₃) = 0

Step 2:

Each π term = m + 1 variables, where m is equal to 3 and also called repeating variables. Out of six variables R, l, V, μ, ρ and K, three variables are to be selected as repeating variables. R is a dependent variable and should not be selected as a repeating variable. Out of the five remaining variables, one variable should have geometric property, the second variable should have flow property and third one fluid property. These requirements are fulfilled by selecting l, V and ρ as repeating variables. The repeating variables themselves should not form a dimensionless term and should have themselves fundamental dimensions equal to m, i.e., 3 here. Dimensions of l, V and p are L, LT^-1, ML^-3 and hence the three fundamental dimensions exist in I, V and ρ and they themselves do not form dimensionless group.

Step 3

Each π-term is written as according to equation (d)

π₁ = l^a₁ . V^b₁ . ρ^c₁ . R
π₂ = l^a₂ . V^b₂ . ρ^c₂ . μ
π₃ = l^a₃ . V^b₃ . ρ^c₃ . K

Step 4:

Each π-term is solved by the principle of dimensional homogeneity.

Dimensional Homogeneity means the dimensions of each terms in an equation on both sides are equal. Thus if the dimensions of each term on both sides of an equation are the same the equation is known as dimensionally homogeneous equation. The powers of fundamental dimensions (i.e., L, M, T) on both sides of the equation will be identical for a dimensionally homogeneous equation. Such equations are independent of the system of units.

For the first π-term, we have

π₁ = M⁰L⁰T⁰
π₁ = L^a₁ . (LT^-1)^b₁ . (ML^-3)^c₁ . MLT^-2

Equating the powers of M, L, T on both sides, we get

Power of M,
0 = c₁ + 1
c₁ = -1

Power of L,
0 = a₁+ b₁ – 3c₁ – 1
a₁ = -b₁ + 3c₁ – 1 = 2 – 3 – 1
a₁ = -2

Power of T,
0 = -b₁ – 2
b₁ = – 2

Substituting the values of a₁, b₁, and c₁ in π₁ equation, we get

π₁ = l^a₁ . V^b₁ . ρ^c₁ . R

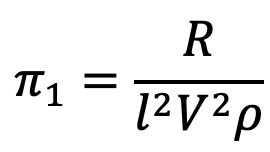
Similarly for the 2nd π-term, we get

π₂ = M⁰L⁰T⁰
π₁ = L^a₂ . (LT^-1)^b₂ . (ML^-3)^c₂ . ML^-1T^-1

Equating the powers of M, L, T on both sides, we get

Power of M,
0 = c₂ + 1
c₂ = -1

Power of L,
0 = a₂+ b₂ – 3c₂ – 1
a₂ = -b₂ + 3c₂ + 1 = 1 – 3 + 1
a₂ = -1

Power of T,
0 = -b₂ – 2
b₂ = – 2

Substituting the values of a₂, b₂, and c₂ in π₂ equation, we get

π₂ = l^-1 . V^-1 . ρ^-1 . μ

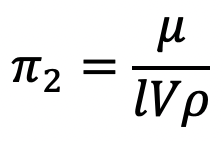
Similarly for the 3rd π-term, we get

π₃ = l^a₃ . V^b₃ . ρ^c₃ . K
π₃ = M⁰L⁰T⁰
π₁ = L^a₃ . (LT^-3)^b₃ . (ML^-3)^c₃ . ML^-1T^-2

Equating the powers of M, L, T on both sides, we get

Power of M,
0 = c₃ + 1
c₃ = -1

Power of L,
0 = a₃+ b₃ – 3c₃ – 1
a₃ = -b₃ + 3c₃ + 1 = 2 – 3 + 1
a₃ = 0

Power of T,
0 = -b₃ – 2
b₃ = – 1

Substituting the values of a₃, b₃, and c₃ in π₃ equation, we get

π₃ = l⁰ . V^-2 . ρ^-1 . K

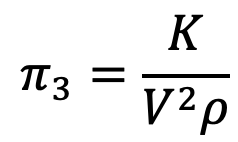
Step 5:

Substituting the values of π₁, π₂, and π₃ in f(π₁, π₂, π₃) = 0 equation, we get

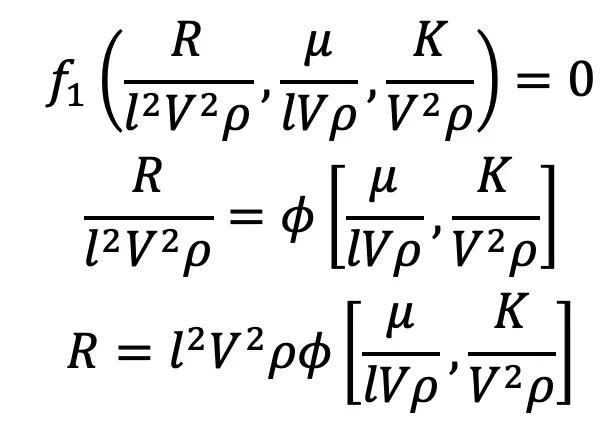
This is all about the Methods of Dimensional Analysis. Let us know what you think about this article in the comment section below.