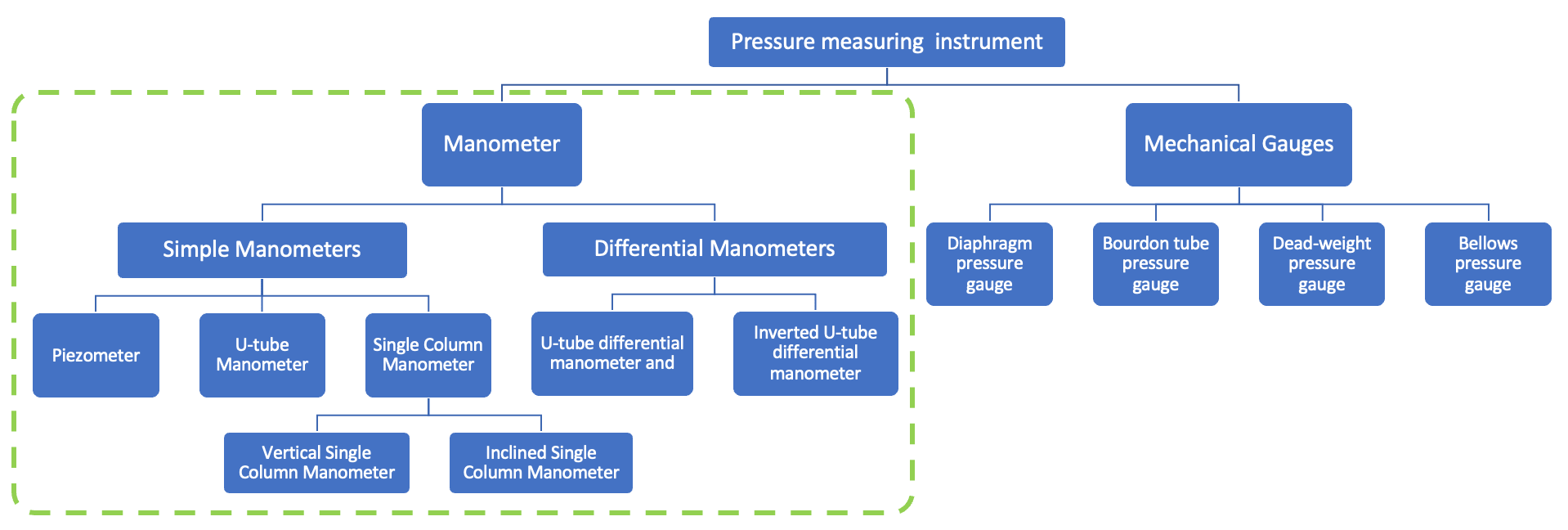
In metrology, there are different types of measuring instruments such as Linear measuring instruments, comparators, Indicators, interferometers and angular measuring instruments. For the measurement of Pressure in Fluids, we use Manometers and mechanical gauges. In this article, we have discussed the broad classification of the Manometers in a detailed manner.

Before getting into the main topic, we want you to understand the units used for the measurement of Pressure in different unit systems. we use the following units for pressure.
The units of pressure are :
In MKS units: kgf/m2 and kgf/cm2
In SI units Newton/m2 or N/m2 and N/mm2 (∴ N/m2 is known as Pascal and is represented by Pa)
Other commonly used units of pressure are :
kPa = kilo pascal = 1000 N/m2
bar = 100 kPa = 105 N/m2
Now we know the units of Fluid Pressure. But how we do take measures of the fluid pressure with instruments and how do they work.
Measurement of Fluid Pressure
The Fluid pressure can be measured by the following instruments:
- Manometers
- Mechanical Gauges.
Let us further classify these two instruments in detail.
Manometers
Manometers are defined as the devices used for measuring the pressure at a point in a fluid by balancing the column of fluid with the same or another column of the fluid.
Manometers are classified as follows
(i) Simple Manometers
(ii) Differential Manometers
Mechanical Gauges
Mechanical gauges are defined as the devices used for measuring the pressure by balancing the fluid column by the spring or dead weight. The commonly used mechanical pressure gauges are :
(a) Diaphragm pressure gauge
(b) Bourdon tube pressure gauge
(c) Dead-weight pressure gauge
(d) Bellows pressure gauge
Let us discuss all these manometers in a detailed manner with the schematic diagrams.
Simple Manometers
A simple manometer consists of a glass tube having one of its ends connected to a point where pressure is to be measured and the other end remains open to the atmosphere. Common types of simple manometers are
- Piezometer,
- U-tube Manometer
- Single Column Manometer
1. Piezometer
Piezometer is the simplest form of manometer used to measure gauge pressures. One end of this manometer is connected to the point where pressure is to be measured and another end is open to the atmosphere as shown in the following.
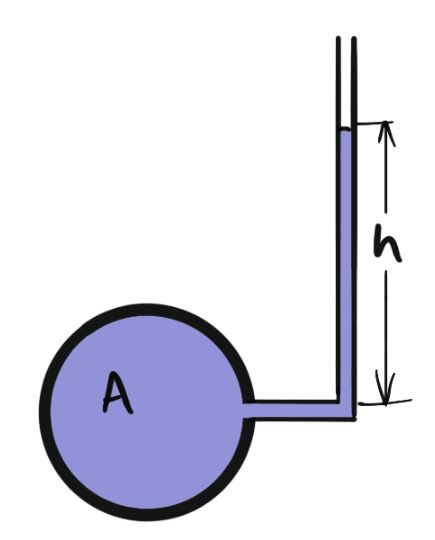
The rise of liquid gives the pressure head at that point. If at point A, the height of liquid say water is h in a piezometer tube, then the pressure at A will be
= ρ × g × h N/m2
2. U-tube Manometer
It consists of a glass tube bent in a U-shape, one end of which is connected to a point at which pressure is to be measured and the other end remains open to the atmosphere as shown in the following figure.
The tube generally contains mercury or any other liquid whose specific gravity is greater than the specific gravity of the liquid whose pressure is to be measured.
(a) For Gauge Pressure
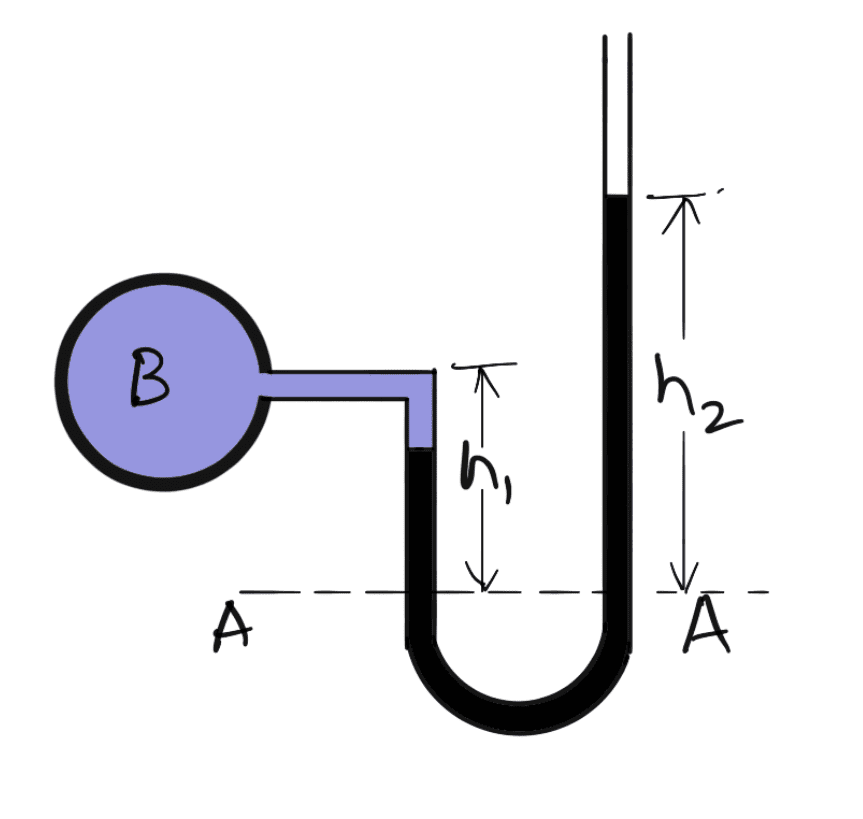
Let B is the point at which pressure is to be measured, whose value is p.
The datum line is A-A.
Let
h1 = Height of light liquid above the datum line
h2 = Height of heavy liquid above the datum line
S1 = Specific gravity of the light liquid
ρ1 = Density of light liquid = 1000 x S1
S2 = Specific gravity of the heavy liquid
ρ2 = Density of heavy liquid = 1000 × S2
As the pressure is the same for the horizontal surface. Hence pressure above the horizontal datum line A-A in the left column and in the right column of the U-tube manometer should be the same.
Pressure above A-A in the left column = p + ρ1 × g × h1
Pressure above A-A in the right column = ρ2 × g × h2
As we said above pressure above the horizontal datum line A-A in the left column and in the right column of the U-tube manometer should be the same, we should equate these two pressures
p + ρ1 × g × h1 = ρ2 × g × h2
p = (ρ2 × g × h2 – ρ1 × g × h1)
(b) For Vacuum Pressure
For measuring vacuum pressure, the level of the heavy liquid in the manometer will be as shown in the following figure
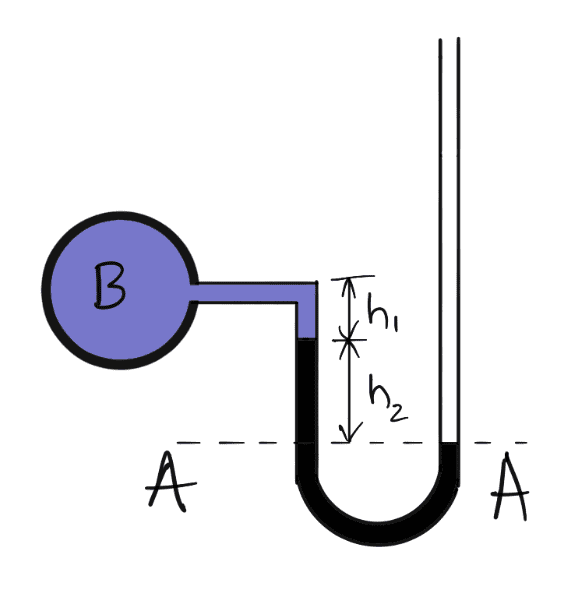
The Pressure above A-A in the left column = ρ2 × g × h2 + ρ1 × g × h1 + p
Pressure head in the right column above A-A = 0
We should equate these two equations, we get
ρ2 × g × h2 + ρ1 × g × h1 + p = 0
p = – (ρ2 × g × h2 + ρ1 × g × h1)
3. Single Column Manometer
The single-column manometer is a modified form of a U-tube manometer in which a reservoir, having a large cross-sectional area (about 100 times) as compared to the area of the tube is connected to one of the limbs (say left limb) of the manometer as shown in the following figure.
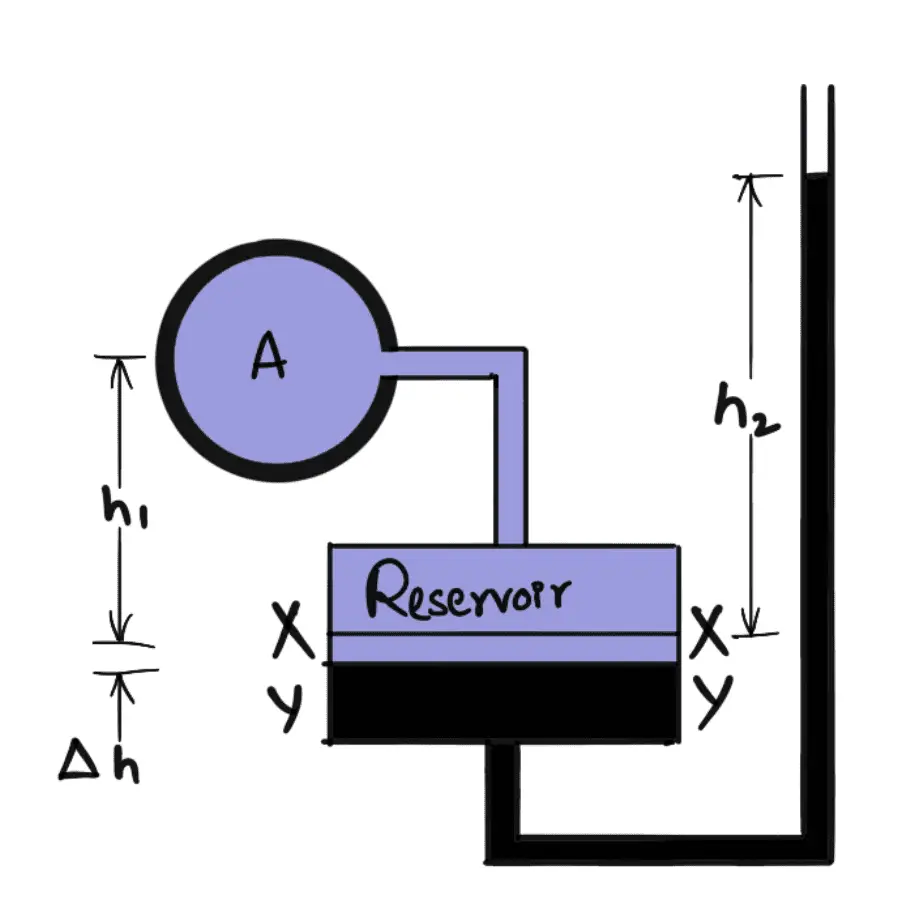
Due to the large cross-sectional area of the reservoir, for any variation in pressure, the change in the liquid level in the reservoir will be very small which may be neglected and hence the pressure is given by the height of liquid in the other limb. The other limb may be vertical or inclined.
Thus there are two types of single-column manometers as
- Vertical Single Column Manometer
- Inclined Single Column Manometer
Vertical Single Column Manometer
The above-given figure is the vertical single-column manometer. Let X-X be the datum line in the reservoir and in the right limb of the manometer when it is not connected to the pipe. When the manometer is connected to the pipe, due to high pressure at A, the heavy liquid in the reservoir will be pushed downward and will rise in the right limb.
Let
Δh = Fall of heavy liquid in the reservoir
h2 = Rise of heavy liquid in the right limb
h1 = Height of centre of pipe above X-X
PA = Pressure at A, which is to be measured
A = Cross-sectional area of the reservoir
a = Cross-sectional area of the right limb
S1 = Specific gravity of liquid in the pipe
S2 = Specific gravity of heavy liquid in reservoir and right limb
ρ1 = Density of liquid in the pipe
ρ2 = Density of liquid in the reservoir
The fall of heavy liquid in the reservoir will cause a rise in heavy liquid levels in the right limb.
A × ∆h = a × h2
∆h = (a × h2)/A
Now consider the datum line Y-Y as shown in the above figure.
The pressure in the right limb above Y – Y = ρ2 × g × (∆h + h2)
The Pressure in the left limb above Y – Y = ρ1 × g × (∆h + h1) + PA
Equating these pressures, we have
ρ2 × g × (∆h + h2) = ρ1 × g × (∆h + h1) + PA
PA = ρ2 × g × (∆h + h2) – ρ1 × g × (∆h + h1)
PA = ∆h(ρ2g – ρ1g) + h2ρ2g – h1ρ1 g
PA = [(a × h2)/A] (ρ2g – ρ1g) + h2ρ2g – h1ρ1 g
This is the equation to
As area A is very large as compared to a, hence ratio a/A becomes very small and can be neglected.
Then
PA = h2ρ2g – h1ρ1 g
From this equation, it is clear that as h1 is known and hence by knowing h2 or rise of heavy liquid in the right limb, the pressure at A can be calculated.
Inclined Single Column Manometer
The following figure shows the inclined single-column manometer. This manometer is more sensitive. Due to inclination, the distance moved by the heavy liquid in the right limb will be more.
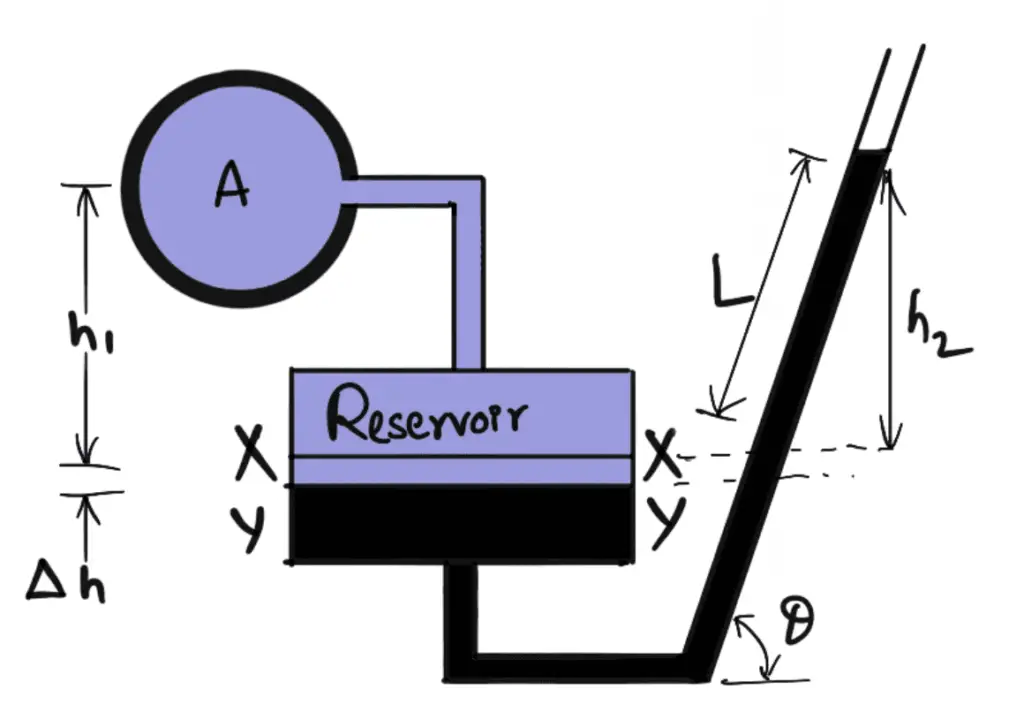
Let
L= Length of heavy liquid moved in the right limb from X-X
θ = Inclination of the right limb with horizontal
h2 = Vertical rise of heavy liquid in the right limb from X-X = L × sin θ
From the above equation, the pressure at A is
PA = h2ρ2g – h1ρ1 g
Substituting the value of h2 we get
PA = L × sin θ × ρ2g – h1ρ1 g
From these relations, we can find the fluid pressure.
Differential Manometers
Differential manometers are the devices used for measuring the difference in pressures between two points in a pipe or in two different pipes. A differential manometer consists of a U-tube, containing a heavy liquid, whose two ends are connected to the points, whose difference in pressure is to be
measured.
The most common types of differential manometers are
- U-tube differential manometer and
- Inverted U-tube differential manometer
1. U-tube Differential Manometer
The following figure shows the differential manometers of the U-tube type
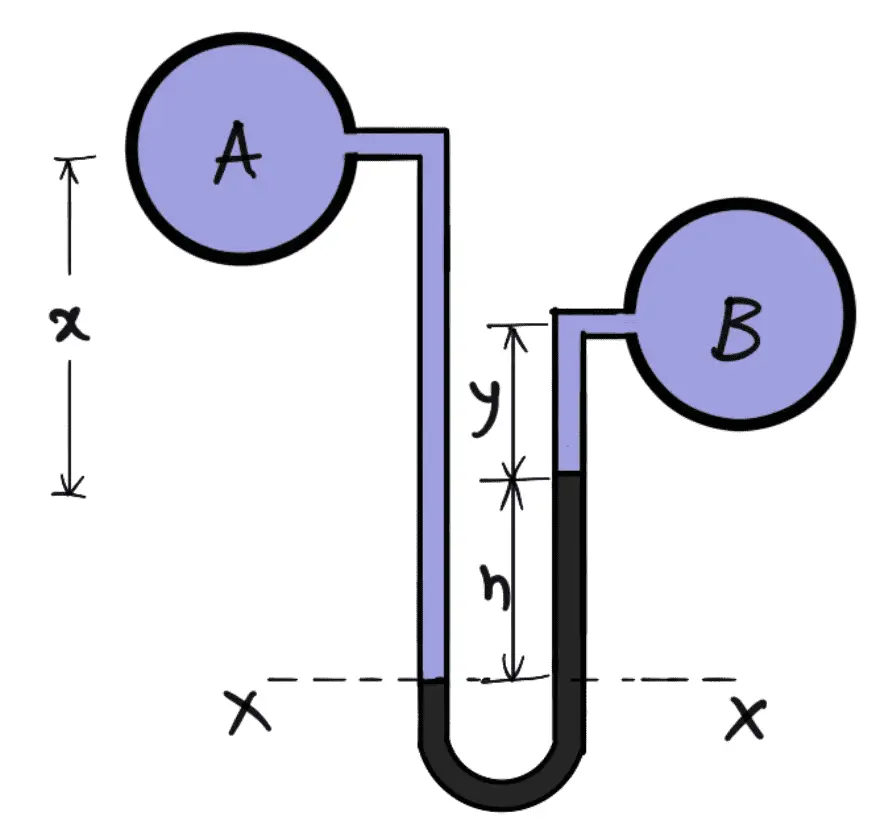
Let the two points A and B are at a different level and also contains liquids of different
Specific Gravity These points are connected to the U-tube differential manometer. Let the pressure at A and B be PA and PB.
Let
h= Difference of mercury level in the U-tube.
y = Distance of the centre of B, from the mercury level in the right limb.
x = Distance of the centre of A, from the mercury level in the right limb.
ρ1 = Density of liquid at A.
ρ2 = Density of liquid at B.
ρg = Density of heavy liquid or mercury
PA = pressure at A
PB = Pressure at B
Let us take the datum line at X-X.
Pressure above X-X in the left limb = ρ1g(h + x) + PA
Pressure above X-X in the right limb = (ρg × g × h) + (ρ2 × g × y) + PB
Equating the two pressure, we have
ρ1g(h + x) + PA = (ρg × g × h) + (ρ2 × g × y) + PB
PA – PB = (ρg × g × h) + (ρ2 × g × y) – ρ1g(h + x)
PA – PB = h × g(ρg – ρ1) + ρ2gy – ρ1gx
Difference of pressure at A and B if they are at different levels PA – PB = h × g(ρg – ρ1) + ρ2gy – ρ1gx
If A and B are at the same level and contain the same liquid of density ρ1.
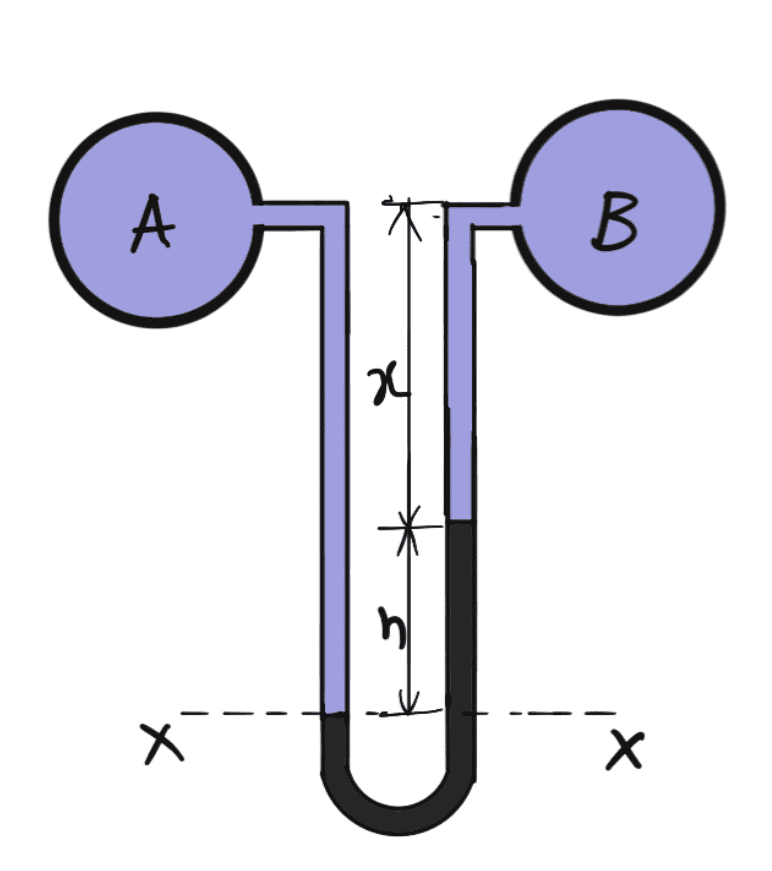
Then the Pressure above X-X in right limb = (ρg × g × h) + (ρ1 × g × x) + PB
Pressure above X-X in left limb = ρ1g(h + x) + PA
Equating the two pressure, we get
(ρg × g × h) + (ρ1 × g × x) + PB = ρ1g(h + x) + PA
PA – PB = (ρg × g × h) + (ρ1 × g × x) – ρ1g(h + x)
PA – PB = h × g(ρg – ρ1) + ρ1gy – ρ1gx
PA – PB = h × g(ρg – ρ1)
Difference of pressure at A and B if they are at the same level PA – PB = h × g(ρg – ρ1).
2. Inverted U-tube Differential Manometer
It consists of an inverted U-tube, containing a light liquid. The two ends of the tube are connected to the points whose difference in pressure is to be measured. It is used for measuring the difference between low pressures.
The following figure shows an inverted U-tube differential manometer connected to the two points A and B. Let the pressure at A is more than the pressure at B.
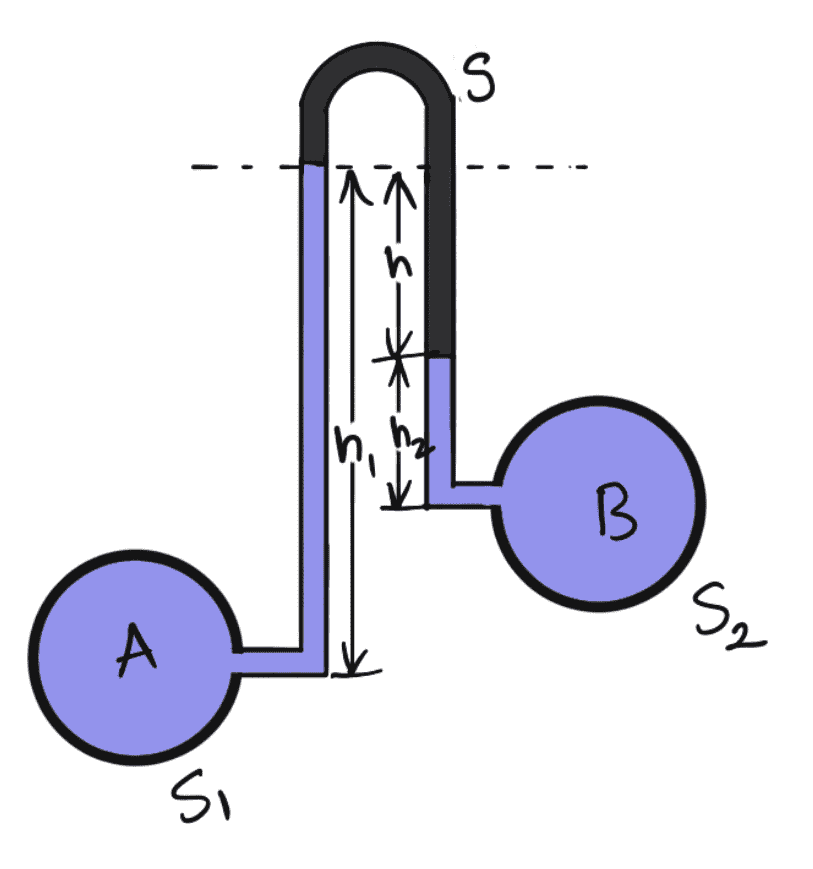
Let
h1 = Height of liquid in left limb below the datum line X-X
h2 = Height of liquid in the right limb
h = Difference between light liquid
ρ1 = Density of liquid at A.
ρ2 = Density of liquid at B.
ρs = Density of light liquid
PA = pressure at A
PB = Pressure at B
Let us take the datum line at X-X.
Pressure above X-X in the left limb = PA – ρ1 × g × h1
Pressure above X-X in the right limb = PB – (ρ2 × g × h2) – (ρs × g × h)
Equating the two pressure, we have
PA – ρ1 × g × h1 = PB – (ρ2 × g × h2) – (ρs × g × h)
PA – PB = (ρ1 × g × h1) – (ρ2 × g × h2) – (ρs × g × h)
Difference of pressure at A and B is PA – PB = (ρ1 × g × h1) – (ρ2 × g × h2) – (ρs × g × h)
Conclusion
We have discussed all the types of manometers used to measure fluids. Let us know what you think about these in the comment section below.

The concept of manometer fully covered well in this post. Instrumentation Engineering students would find this article very useful.