Among the basic components of an Internal Combustion engine, the Push rod is one of the critical components. The push rods are used in overhead valve and side valve engines. Since these are designed as long columns, therefore Euler’s formula should be used. The push rods may be treated as pin-end columns because they use spherical seated bearings. Let us see how we can Design Push rods for an internal combustion engine.

Let
W = Load acting on the push rod
D = Diameter of the push rod
d = Diameter of the hole through the push rod,
I = Moment of inertia of the push rod
= (π/64) × D4 , for solid rod
= (π/64) (D4 – d4), for tubular section
l = Length of the push rod
E = Young’s modulus for the material of the push rod
If m is the factor of safety for the long columns, then the critical or crippling load on the rod is given by
Wcr = m × W
Now using following Euler’s formula the diameter of the push rod (D) can be obtained.
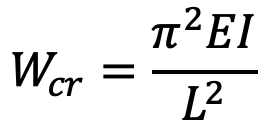
Notes:
- Generally, the diameter of the hole through the push rod is 0.8 times the diameter of the push rod, i.e. d = 0.8 D
- Since the push rods are treated as pin end columns, therefore the equivalent length of the rod (L) is equal to the actual length of the rod ( l ).
Example Problem to Design Push Rods
Problem Statement: The maximum load on a petrol engine push rod 300 mm long is 1400 N. It is hollow having an outer diameter of 1.25 times the inner diameter. Spherical seated bearings are used for the push rod. The modulus of elasticity for the material of the push rod is 210 kN/mm2. Find a suitable size for the push rod, taking a factor of safety of 2.5.
Answer:
Length of push rod l = 300 mm
Maximum load on Push rod is W = 1400 N
Outer Diameter of the push rod D = 1.25 d
Modulus of elasticity E = 210 kN/mm2 = 210 × 103 N/mm2
The factor of safety m = 2.5
Moment of inertia of the push rod section,
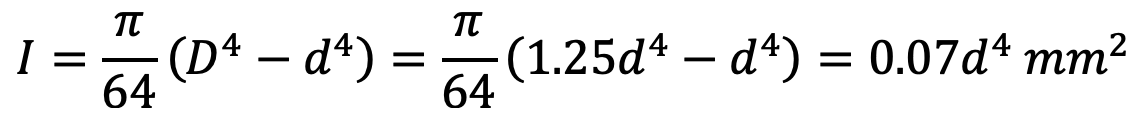
We know that the crippling load on the push rod,
Wcr = m × W = 2.5 × 1400 = 3500N
Now according to Euler’s formula, crippling load (Wcr),
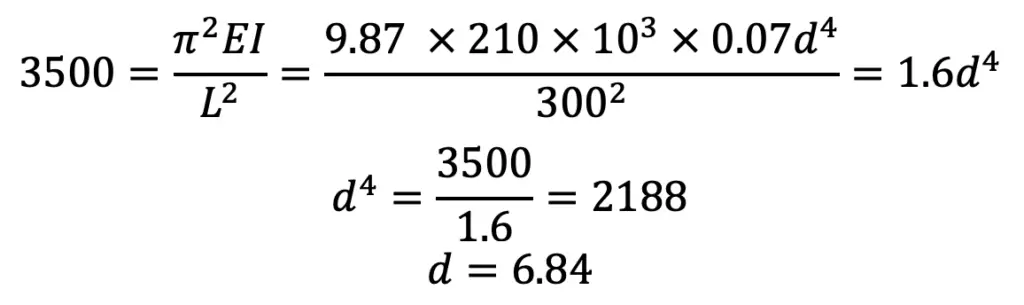
The inner diameter of the push rod d = 6.84mm
The outer diameter of the push rod D = 1.25 d = 1.25 × 6.84 = 8.55 mm
This is how we can determine the diameters from Euler’s formula to design push rods. Let us know what you think about this article in the comment section below.

Leave a Reply