We have discussed belt drives and rope drives that slipping may occur. To avoid slipping, steel chains are used. The chains are made up of a number of rigid links which are hinged together by pin joints to provide the necessary flexibility for wrapping around the driving and driven wheels. These wheels have projecting teeth of special profile and fit into the corresponding recesses in the links of the chain. The toothed wheels are known as sprocket wheels or simply sprockets (These wheels resemble spur gears). The sprockets and the chain are thus constrained to move together without slipping, ensuring a perfect velocity ratio. We have already discussed Chain Drive Terminology, Classification, and Advantages in the previous article. Let us discuss how we can calculate Length of Chain and Centre Distance.

Chain Drive: Chains and Sprockets
The chains are mostly used to transmit motion and power from one shaft to another when the center distance between their shafts is short such as in bicycles, motorcycles, agricultural machinery, conveyors, rolling mills, road rollers, etc. The chains may also be used for long center distances of up to 8 meters. The chains are used for velocities up to 25m/s and power up to 110 kW. In some cases, higher power transmission is also possible.
Following is a schematic Representation of a Chain Drive that comprises Sprockets and a chain.
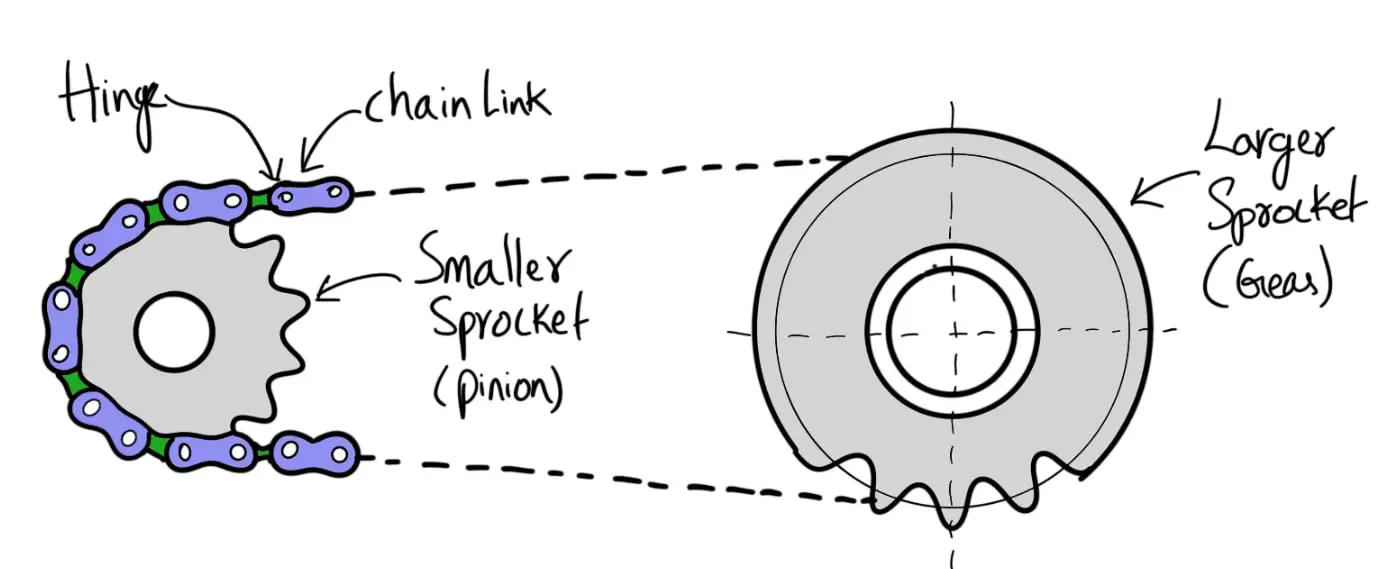
Length of Chain and Centre Distance
Following is an open chain drive system connecting the two sprockets.
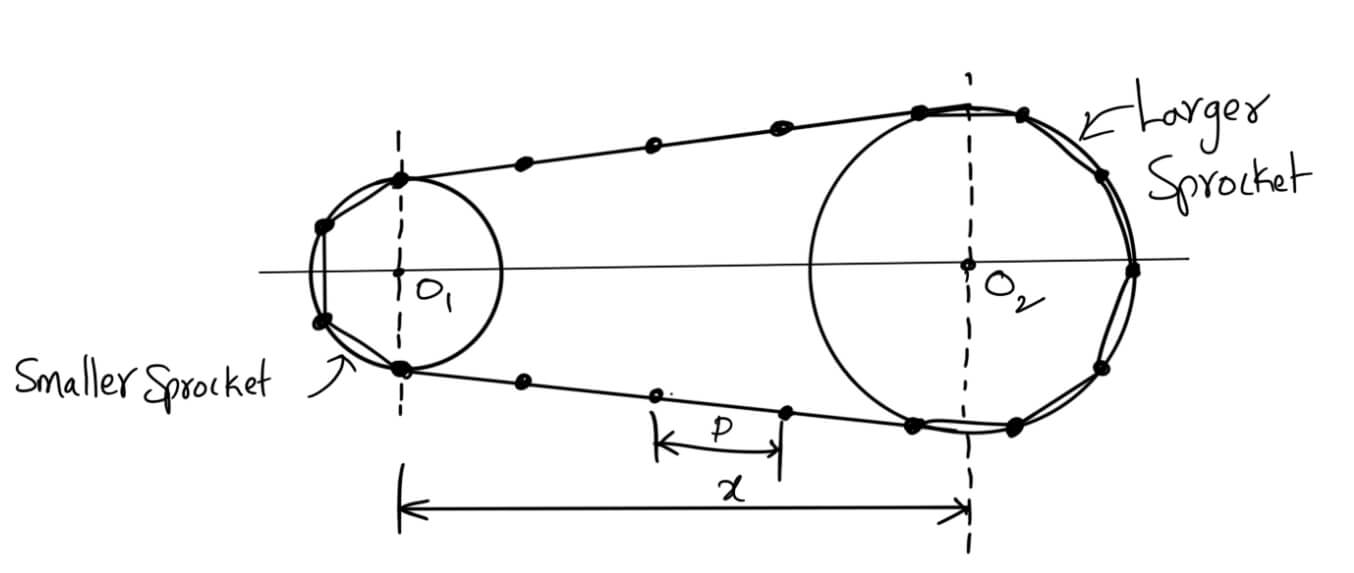
Let
T1 = Number of teeth on the smaller sprocket
T2 = Number of teeth on the larger sprocket
p = Pitch of the chain
x = Centre distance
The length of the chain (L) must be equal to the product of the number of chain links (K) and the pitch of the chain (p).
Mathematically,
L = K.p
The number of chain links may be obtained from the following expression, i.e.
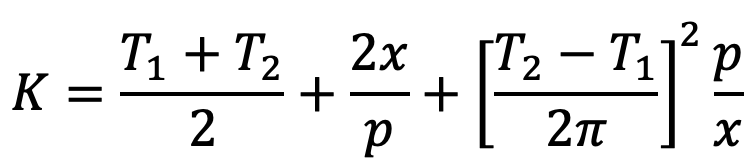
The value of K as obtained from the above expression must be approximated to the nearest even number.
The center distance is given by
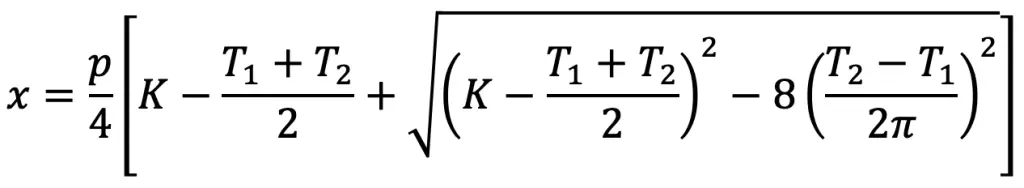
To accommodate the initial sag in the chain, the value of the center distance obtained from the above equation should be decreased by 2 to 5 mm.
- The minimum center distance for the velocity transmission ratio of 3, may be taken as
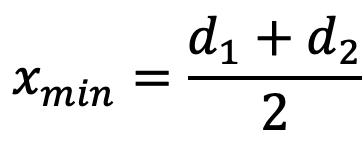
where d1 and d2 are the diameters of the pitch circles of the smaller and larger sprockets.
- For best results, the minimum center distance should be 30 to 50 times the pitch.
- The minimum center distance is selected depending on the velocity ratio so that the arc of contact of the chain on the smaller sprocket is not less than 120∘. It may be noted that a larger angle of the arc of contact ensures a more uniform distribution of load on the sprocket teeth and better conditions of engagement.
Velocity Ratio of Chain Drives
The velocity ratio of a chain drive is given by
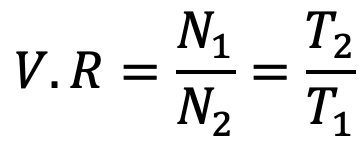
Where
N1 = Speed of rotation of smaller sprocket in r.p.m
N2 = Speed of rotation of larger sprocket in r.p.m
T1 = Number of teeth on the smaller sprocket
T2 = Number of teeth on the larger sprocket
The average velocity of the chain is given by
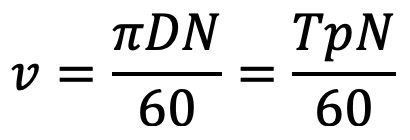
Where
D = Pitch circle diameter of the sprocket in meters
p = Pitch of the chain in meters
This is all about how we can calculate the Length of Chain and velocity of chain drives. Let us know what you think about this article in the comment section below.

Leave a Reply