How to calculate Fatigue Life?

As we discussed earlier What is fatigue failure. Fatigue failure refers to the failure of the machine component due to repeated or cyclic loading. These cyclic or repeated loads are known as fatigue loads. Due to the fluctuation in the stress, this Fatigue failure occurs. Fatigue life means the number of cycles of stress that a component can withstand before failure is known as Fatigue life. Let us see how we can calculate Fatigue life.

Many types of tests are used to determine the fatigue life of a material. The most commonly used small-scale fatigue test is the rotating-beam test in which a specimen is subjected to alternating compression and tension stresses of equal magnitude while being rotated. This is rotating beam test is explained briefly in here.

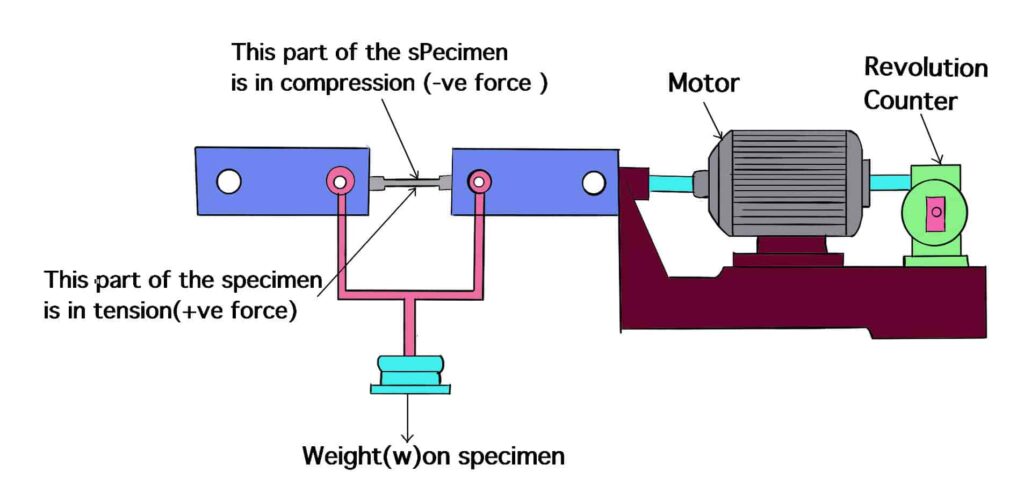
Fatigue Life Calculation

While designing a new engineering component using a particular material, it is desirable to obtain information about the fatigue life of the part. This can be done in many cases by combining fracture toughness data with fatigue crack growth data to produce an equation that can be used to predict fatigue life.

One type of equation for calculating fatigue life can be developed by integrating the fatigue crack growth rate equation between an initial crack (flaw) size a_o and the critical crack (flaw) size a_f, which is produced at fatigue failure after the number of cycles to failure N_f.

The Fatigue Crack Growth Rate equation is given below,

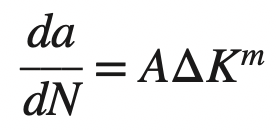
Where
da/dN = fatigue crack growth rate, (Units: mm/cycle or in./cycle)
ΔK = stress-intensity factor range (ΔK = K_max − K_min ), MPa√m or ksi√in
A, m = constants that are a function of the material, environment, frequency, temperature, and stress ratio

Here we used the Stress intensity facto K_I (pronounced “Kay-one”) for mode 1.

Not the critical stress intensity factor K_IC (pronounced “kay-one-see”) called the Fracture toughness. It should not be confused. It needs to be understood from here.

We know the stress intensity factor for Mode 1

K_I = Y σ √(πa)

K_I = stress-intensity factor 
σ = applied nominal stress
a = edge crack length or half the length of an internal through the crack
Y = dimensionless geometric constant of the order of 1

We know that the stress intensity factor can be written as follows

ΔK = Yσ√πa = Y σ π^1/2 a^1/2

It follows that

ΔK^m = Y^m σ^m π^m/2 a^m/2

Substituting this value in the above Fatigue Crack Growth Rate equation, we will get

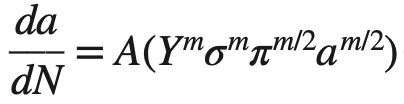
After rearranging the above equation, we integrate the crack size from the initial crack size a_o to the final crack size at failure a_f and the number of fatigue cycles from zero to the number at fatigue failure N_f. Thus,

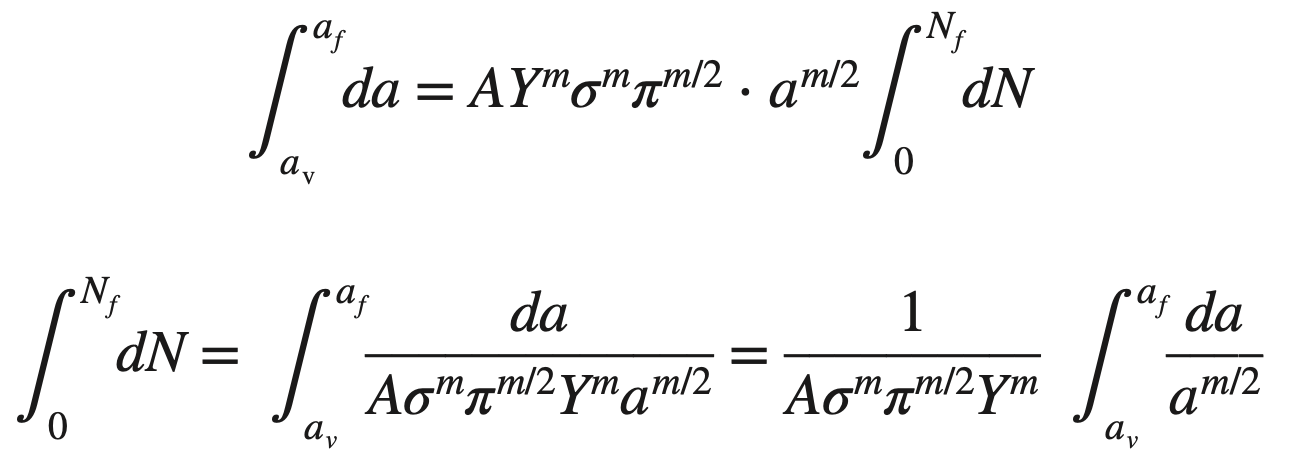
We know a standard integration formula as follows

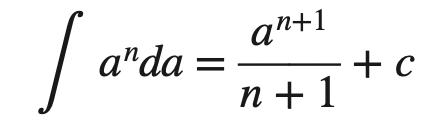
We also can write the following standard integration formula

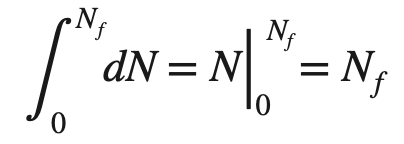
We can re-write the above equation by substituting the above two formulas

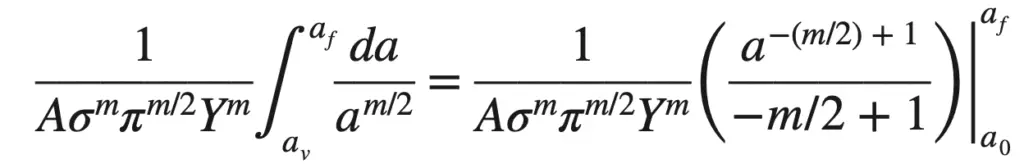
If we can rearrange the above relation to get the fatigue life in cycles N_f, we get as follows

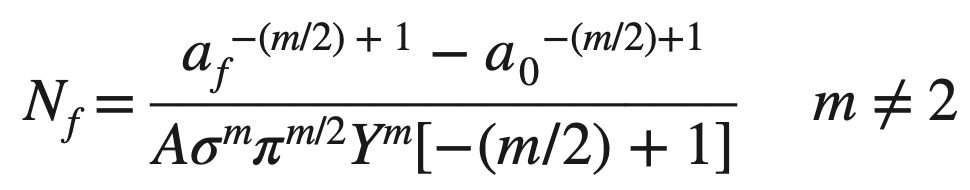
This is the Fatigue life formula. This equation assumes that m ≠ 2 and that Y is independent of the crack length, which is not usually the case.

Thus, the above fatigue life in cycles N_f may or may not be the true value for the fatigue life of the component.

For the more general case, Y = f (a), the calculation of N_f must take into account the change in Y, and so ΔK and ΔN must be calculated for small successive amounts of length.

Let us solve an example problem to How to calculate the Fatigue Life of a steel plate subjected to a constant tensile and compressive test using a fatigue testing machine.

Example problem to calculate Fatigue Life

An alloy steel plate is subjected to constant-amplitude uniaxial fatigue cyclic tensile and compressive stresses of magnitudes of 120 and 30 MPa, respectively. The static properties of the plate are a yield strength of 1400 MPa and a fracture toughness K_IC of 45 MPa√m. If the plate contains a uniform through-thickness edge crack of 1.00 mm, how many fatigue cycles are estimated to cause fracture? Use the equation da/dN (m/cycle) = 2.0 × 10^-12ΔK³ (MPa√m). Assume Y = 1 in the fracture toughness equation.

Answer:

Given data
da/dN (m/cycle) = 2.0 × 10^-12ΔK³ (MPa√m)
A = 2.0 × 10^-12
m = 3,
σ_r = (120 − 0) MPa (since compressive stresses are ignored)
Y = 1
K_IC = 45 MPa√m

The initial crack size a_o is equal to 1.00 mm.

The final crack size a_f is determined from the fracture toughness equation

We know the Fracture toughness formula K_IC = Y σ_r √(πa_f)

45 MPa√m = 1 × 120 MPa × √(πa_f)

Solving this we get the final crack size a_f = 0.0449m

Now we need to find out the fatigue life in cycles N_f from the above-given equation.

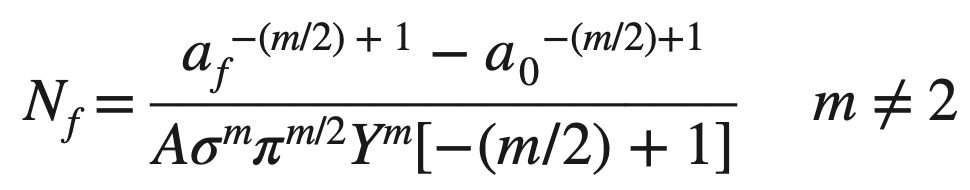
Let us substitute all the available values in the above equation to calculate the fatigue life in cycles N_f

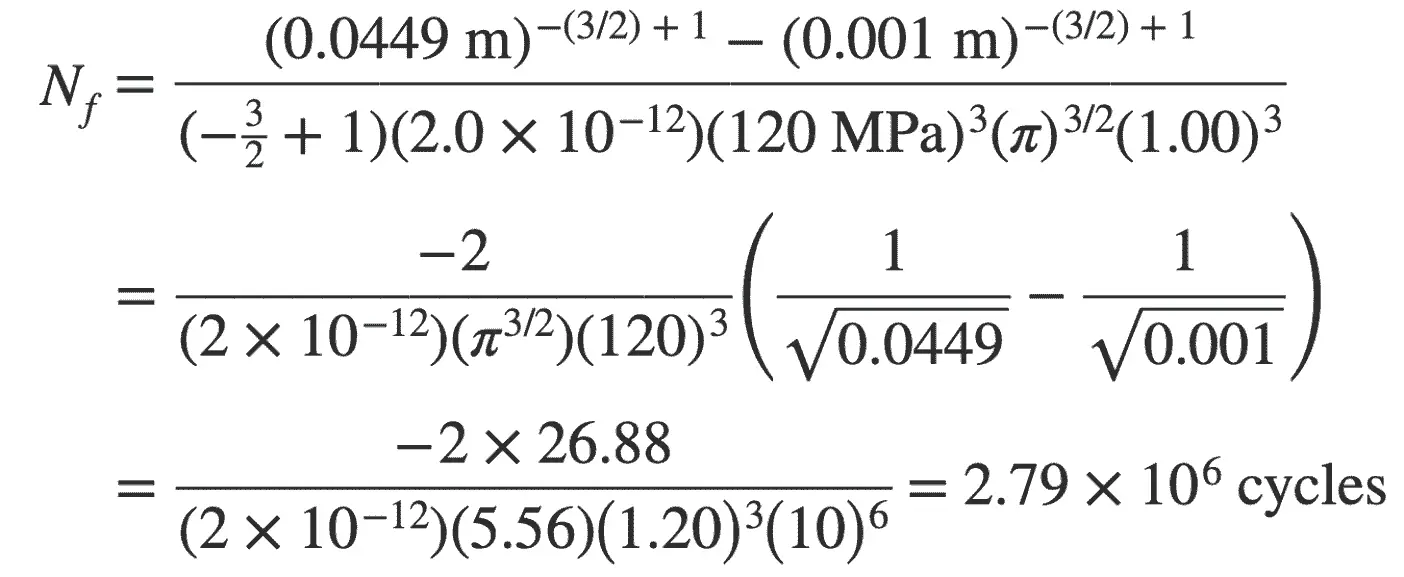
We got the fatigue life in cycles N_f as 2.79 × 10⁶ cycles.

This is how we can calculate the fatigue life in cycles N_f for any machine component under repeated loads.

Conclusion

We have discussed how to calculate the fatigue life of any component in terms of cycles. Among the other material failures, Fracture failure, and fatigue failure and Creep failure are observed in the testing stage of prototypes. All these concepts are very important for every design engineer should have a deep understanding of.