Torsional shear stress or Torsional stress is the shear stress produced in the shaft due to the twisting. This twisting in the shaft is caused by the couple acting on it. What is a couple? How can shear stress in the shaft be produced? Let’s get into the subject.

Shear Stress in Shafts
Twisting can be produced in the shaft when two equal and opposite couples acting in parallel planes.
A couple is Two equal and opposite parallel forces acting upon a body with a different line of acting points said as a couple. (the Following figure represents how a twisting is produced when tightening of a nut with a wrench)
When a machine member is under the twisting force then it is said to be the shaft is subjected to torsion.
Due to this torsion in the shaft, the stresses induced in the shaft are known as the Torsional shear stress or simply Torsional stress.
Torsional Shear stress/ Torsional Stress
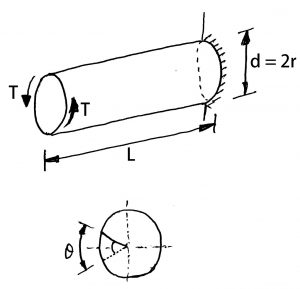
Consider a shaft is fixed at one end and another end is subjected to the torque as shown in the figure. As a result, each and every cross section of the shaft is subjected to the Torsional shear stress.
Due to the Circular section of the shaft, It has been considered that the shear stress at the centre axis will be zero and it is maximum at the outer surface of the shaft.
From the Torsion equation for a circular member is
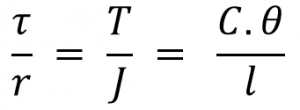
Where
τ = Torsional stress induced at the outer surface of the shaft (Maximum Shear stress)
r = Radius of the shaft
T = Twisting Moment or Torque
J = Polar moment of inertia
C = Modulus of rigidity for the shaft material.
l = Length of the shaft
θ = Angle of twist in radians on a length “l”
Torsion Equation Assumptions
This torsion equation is base on the following assumptions
- Uniform material through the shaft. (The material should be homogeneous, isotropic and elastic)
- Unifrom distribution of twisting force along the length of the shaft.
- Twisting force under elastic limit
- The cross-section of the shaft is considered as the planar and circular both before and after twist.
- The distance between the two normal section is the same in both before and after the twist.
From Torsion Equation we can assume
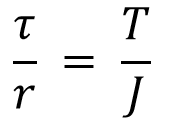
We can calculate the Torsional shear stress from this form
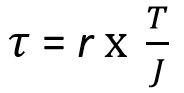
We can also find other unknown factors like the twist in the shaft, torsion force or the polar moment of inertia from the Torsion equation.
Conclusion
The ability to resist the torsion is known as the torsional stiffness. The measure of the torsional stiffness is known as the polar moment of inertia.
From this, the torsional rigidity can be defined as the product of the polar moment of inertia and the Rigidity of shaft material.
Torsion Rigidity = C x J
Where
J = Polar moment of inertia
C = Modulus of rigidity for the shaft material.



Leave a Reply