The Fluids that have higher viscosity are known as viscous fluids and they will have very less velocity flow. The most common and general example of viscous fluid is honey, grease and oil. We have been discussing kinematics and the dynamics of the fluid. We already discussed the Loss of Head of a viscous fluid flow in a circular pipe and Viscous fluid between two parallel plates. This article will discuss The Loss of Head Due to Friction in Viscous Flow.

Viscous Fluid Flow
As we already mentioned Fluids that have higher viscosity are known as viscous fluids and they will have significantly less velocity flow. At low velocity the fluid moves in layers. Each layer of fluid slides over the adjacent layer.
From the previous article, The study of Flow of Viscous Fluid in a Pipe, we understood the shear stress distribution, the velocity distribution and the Drop of Pressure head for a given Length (L) of a pipe.
We are going to use the very same equation (f), from that article. That equation is also known as the Hagen Poiseuille Formula.
Loss of Head Due to Friction in Viscous Flow
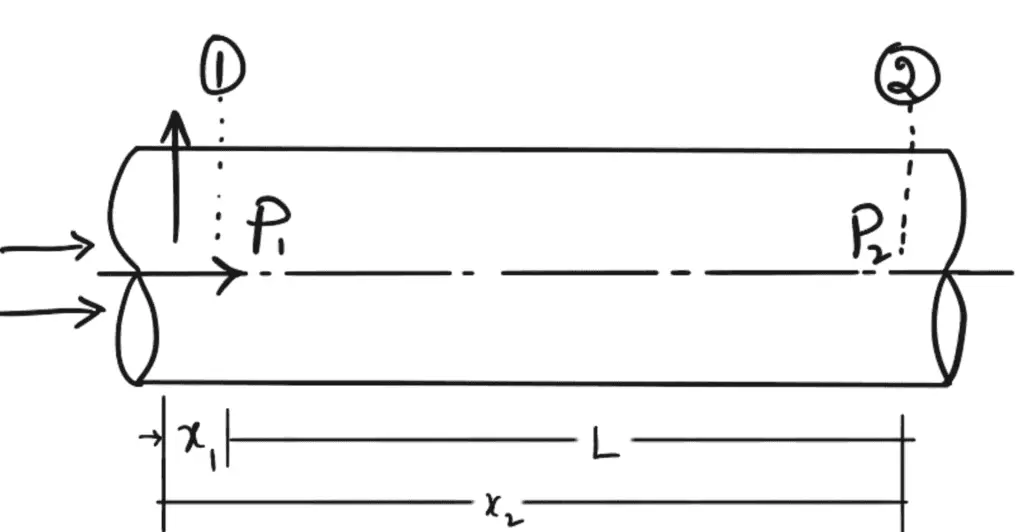
The loss of pressure head, hf, in a pipe of diameter D, in which a viscous fluid of viscosity μ is flowing with a velocity ū is given by the Hagen Poiseuille formula from the equation (f) is
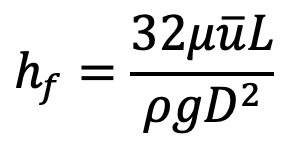
Where L is the length of the pipe.
The loss of head due to friction is given by
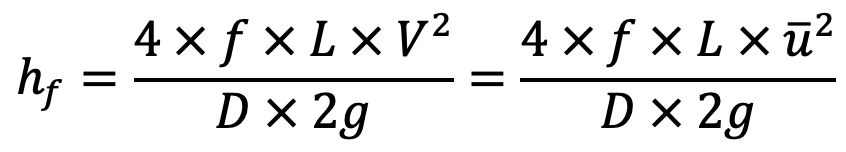
where f = coefficient of friction between the pipe and fluid.
The velocity in the pipe can be always considered as the average velocity: V = ū
Let us equate these two equations (f) and (g)
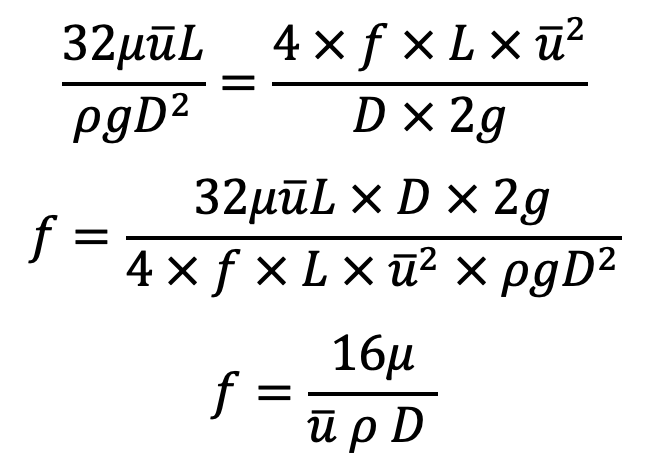
We know
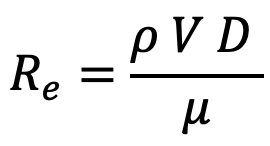
We can write
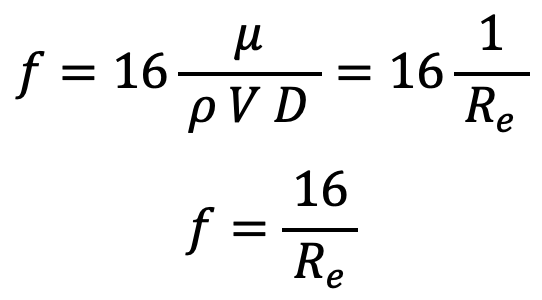
This is the equation that helps us calculate the coefficient of friction between the pipe and the fluid.
Example Problems on Pressure Head lost due to friction
We can calculate the Pressure Head lost due to friction in Viscous Flow and the shear stress at the pipe wall and the fluid.
Problem Statement: A pipe of diameter 20 cm and length 104m is laid at a slope of 1 in 200. An oil of specific gravity 0.9 and viscosity 1.5 poise is pumped up at the rate of 20 litres per second. Find the head lost due to friction. Also calculate the power required to pump the oil.
Answer:
Diameter of pipe D = 20cm = 0.2 m
Area = πD2/4 = π(0.2)2/4 = 0.0314mm2
Length of pipe = L = 10000 m
Slope of pipe i = 1 in 200 =1/200
Specific Gravity of Oil = 0.9
Density of oil ρ = 0.9 × 1000 = 900 kg/m3
Viscosity of oil μ = 1.5 poise = 1.5/10 N/m2
Discharge Q = 20 liter/s = 0.02 m3/s
Velocity Flow ū = Q / Area = 0.02/0.0314 = 0.6366 m/s
Reynolds number
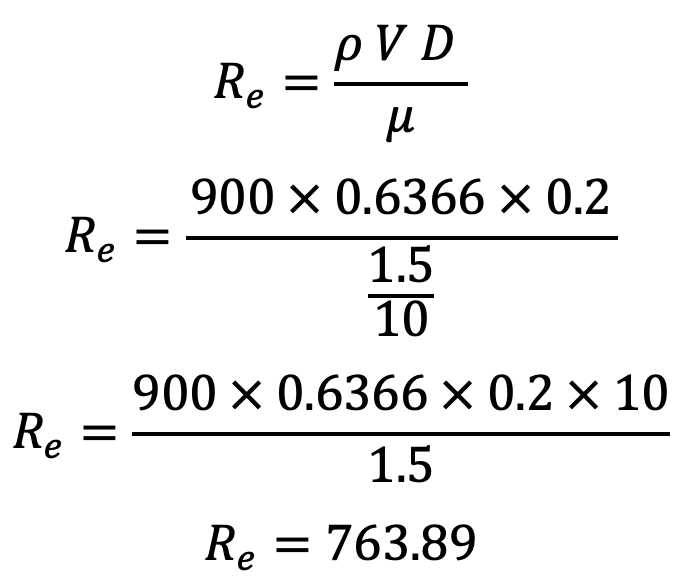
As the Reynolds number is less than 2000, the flow is viscous. The coefficient of friction for viscous flow is given by equation (h) as
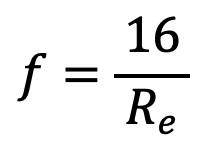
f = 16/763.89
f = 0.02094
Head lost due to friction
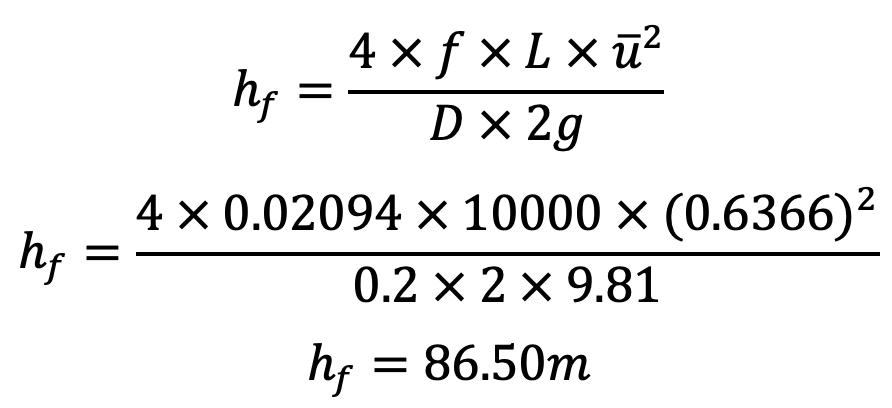
hf = 86.5m
Due to slope of pipe 1 in 200, the height through which oil is to be raised by pump = Slope x Length of pipe
= i × L
= 1/200 × 10000
= 50m
Total head against which pump is to work
H = hf + i × L
H = 86.50 + 50
H = 136.50 m
Power required to pump the oil
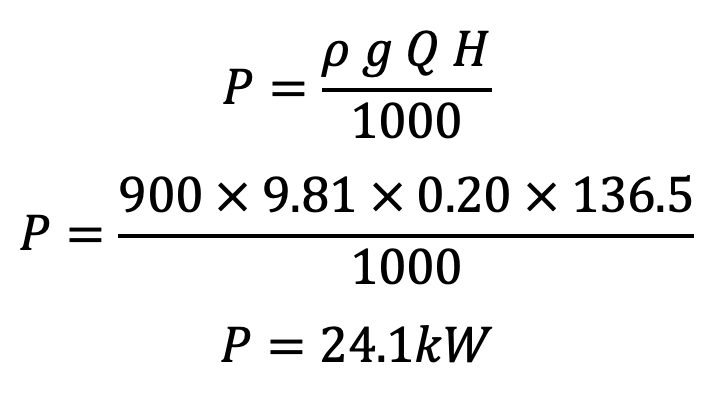
This is how we can calculate the loss of pressure head and the power required to pump the oil through the pipe.
Let us now solve another example where we can calculate the shear stress.
Problem Statement: Water is flowing through a 200 mm diameter pipe with coefficient of friction f = 0.04. The shear stress at a point 40 mm from the pipe axis is 0.00981 N/cm2. Calculate the shear stress at the pipe wall.
Answer:
Dia. of pipe D = 200 mm = 0.20m
Coefficient of friction f = 0.04
Shear stress (at r = 40 mm) τ = 0.00981 N/cm2
Let the shear stress at pipe wall = τ0
First find whether the flow is viscous or not. The flow will be viscous if Reynolds number R, is less than 2000.
Using equation (h), we get
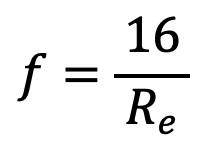
Re = 16/ 0.4
Re = 400
This means flow is viscous.
From this article, The shear stress in case of viscous flow through a pipe is given by the equation (a) as
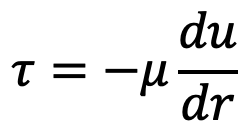
But ∂p/∂x is constant across a section. Across a section, there is no variation of r and there is no variation of p.
τ ∝ r
At the pipe wall, radius = 100 mm and shear stress is τ0
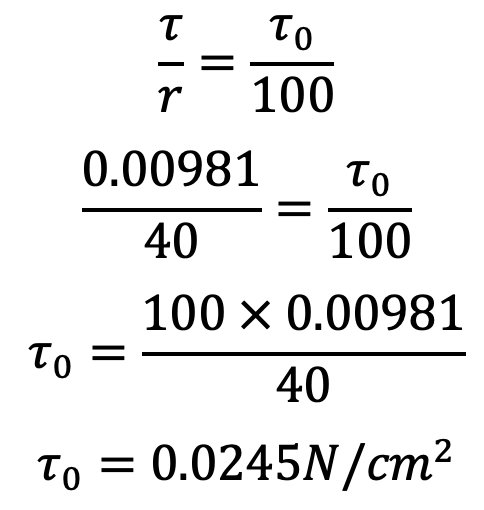
The shear stress at the pipe wall τ0 is 0.0245 N/cm2
This is all about the loss of Head due to friction in the viscous flow in a pipe Let us know what you think about this article in the comment section below.

Leave a Reply