Welding Joint Stresses and Stress Concentration Factors

In the previous article, we have discussed how discussed different welding processes Arc welding TIG welding, MIG welding, Gas welding, also have discussed how to calculate the welding joint strength. Let us discuss welding joint stresses and different stress concentration factors for the Welded joints.

Welding Joint Stress

Welding joint stresses are difficult to determine because of the variable and unpredictable parameters. Those parameters are homogeneity of the weld metal, thermal stresses in the welds, heat treatment due to the Heat Affected zones, and changes of physical properties due to the high rate of cooling.

The Welding joint stresses can be obtained by assuming the following assumptions while the welded joint is under load.

1. The load is distributed uniformly along the entire length of the weld
2. The stress is spread uniformly over its effective section.

The following table shows the allowable stresses for welded joints for joining ferrous metals with mild steel electrodes under steady and fatigue or reversed load.

	Bare Electrode	Bare Electrode	Coated Electrode	Coated Electrode
Types of Weld	Steady Load (Mpa)	Fatigue Load (Mpa)	Steady Load (Mpa)	Fatigue Load (Mpa)
Fillet Welds (all types)	80	21	98	35
Butt welds for Tensiile load	90	35	110	55
Butt Weld for compression Load	100	35	125	55
Butt welds for Shear load	55	21	70	35

The above data is a standard handbook data that can be utilized for simple weld joint stress calculation.

Stress Concentration Factor for Welded Joints

Stress concentration occurs due to irregular stress distribution. This irregular stress distribution occurs in a welding joint due to the irregular welded joint.

The reinforcement provided to the weld produces stress concentration at the junction of the weld and the parent metal. When the parts are subjected to fatigue loading, the stress concentration factor for different Welding joints as given in the following table should be taken into account.

Type of Welding Joint	Stress Concentration Factor
Reinforced butt Joint	1.2
Toe of Transverse Fillet Joint	1.5
End of Parallel Filled Weld	2.7
T-Butt Joint with a sharp corner	2

The above-listed factors for the fatigue loading. For static loading on the welded joint, the stress concentration factor is 1.0.

Now let us solve a simple problem to calculate the Welding joint Stresses from the above-mentioned stress concentration factors and the allowable Welding joint stresses.

Example problem to find Welding Joint length of given specimen

A plate 100 mm wide and 12.5 mm thick is to be welded to another plate by means of parallel fillet welds. The plates are subjected to a load of 50 kN. Find the length of the weld so that the maximum stress does not exceed 56 MPa. Consider the joint first under static loading and then under fatigue loading.

Solution:

Given data
Width = 100mm
Thickness = 12.5mm = This is the size of the weld (s)
Load = 50 kN = 50 × 10³N
Max allowable stress (τ) = 56 MPa = 56 N/mm²

Let us say l is the length of the weld which needed to be determined.

Static Loading

For static loading we have the max allowable stress (τ) = 56 MPa/1.0 = 56 N/mm²

Where 1 is the stress concentration factor that needs to be used every time we design a weld joint.

So from the previous article, for a double parallel fillet joint, the maximum load (P) which the plates can withstand is given by (from Equation 2)

P = 1.414 s × l × τ

50×10³ =1.414 s × l × τ
50×10³ = 1.414 × 12.5 × l × 56
50×10³ = 990 l 
l = 50 × 10³ / 990
l = 50.5 mm

Adding 12.5 mm for starting and stopping of weld run, we get

l = 50.5 + 12.5 = 63mm

For withstanding a stating load of 50 kN the plate should be welded with a double parallel fillet joint with a length of 63mm.

Fatigue Loading

And for fatigue loading we have the max allowable stress (τ) = 56 MPa/2.7 = 20.74 N/mm²

P = 1.414 s × l × τ

50×10³ =1.414 s × l × τ
50×10³ = 1.414 × 12.5 × l × 20.74
50×10³ = 367 l 
l = 50 × 10³ / 367
l = 136.2 mm

Adding 12.5 mm for starting and stopping of weld run, we get

l = 136.2 + 12.5 = 148.7mm

For withstanding a fatigue load of 50 kN the plate should be welded with a double parallel fillet joint with a length of 149mm.

Solve this Example problem to find Welding Joint length of given specimen on your own.

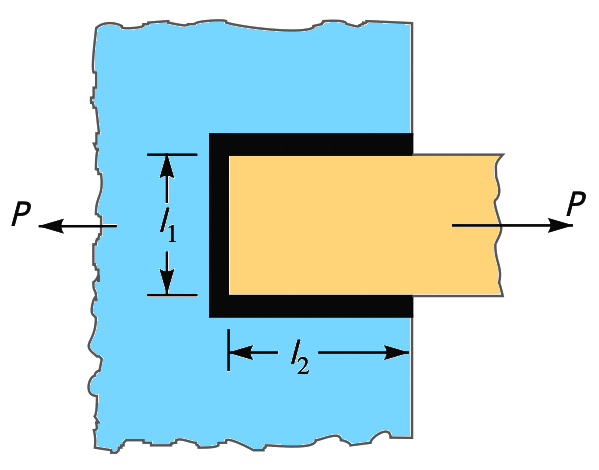
A plate 75 mm wide and 12.5 mm thick is joined with another plate by a single transverse weld and a double parallel fillet weld as shown in Fig. 10.15. The maximum tensile and shear stresses are 70 MPa and 56 MPa respectively. Find the length of each parallel fillet weld, if the joint is subjected to both static and fatigue loading.

Use the formulas from this article to solve and Let us know the answer in the comments box!

Conclusion

This is how the stress concentration factors for the weld joints are taken into consideration in calculating the welding strengths. And also the allowable welding joint stress is given above for your reference which is the mandatory input for calculating welding joint length or strength. Solve the above example problem and Let us know what answer you get in the comment section below.