The Study of Viscous Fluid between two Parallel Plates

We have been discussing kinematics and the dynamics of the fluid. In this article, we will discuss the study of the flow of the Viscous Fluid between two Parallel Plates. The Fluids that have higher viscosity are known as viscous fluids and they will have very less velocity flow. The most common and general example of viscous fluid is honey, grease and oil. Let us discuss more details such as the Shear stress distribution of viscous fluid, velocity distribution and the drop of the pressure head for a given length of Viscous Fluid between two Parallel Plates

Viscous Flow

As we already mentioned Fluids that have higher viscosity are known as viscous fluids and they will have very less velocity flow. At low velocity the fluid moves in layers. Each layer of fluid slides over the adjacent layer.

Due to the relative velocity between two layers the velocity gradient du/dy exists and hence the shear stress acts on the layer will be

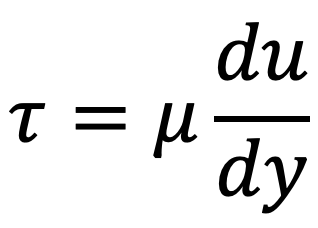
Following are these different scenarios, we shall be discussing to study the flow of viscous fluid

1. The flow of viscous fluid through a circular pipe
2. The flow of viscous fluid between two parallel plates
3. Kinetic energy correction and momentum correction factors
4. Power absorbed in viscous flow through
   • Journal bearings
   • Foot-step bearings
   • Collar bearings

In the previous article, we have already discussed The study of the Flow of Viscous Fluid in a Pipe with the shear stress distribution, velocity distribution and the drop of the pressure head in the length of the pipe.

In this article, we will discuss the flow of viscous fluid between two parallel plates in a detailed manner with the viscous fluid velocity distribution and the drop of the pressure for a given length.

Flow of Viscous Fluid between Two Parallel Plates

In The flow of viscous fluid between two parallel plates, the same attributes will be calculated as similar to the previous article.

• Shear stress distribution of Viscous Fluid between two Parallel Surfaces
• Velocity distribution across a section
• The ratio of maximum velocity to the average velocity
• Difference of pressure head for a given length of parallel plates

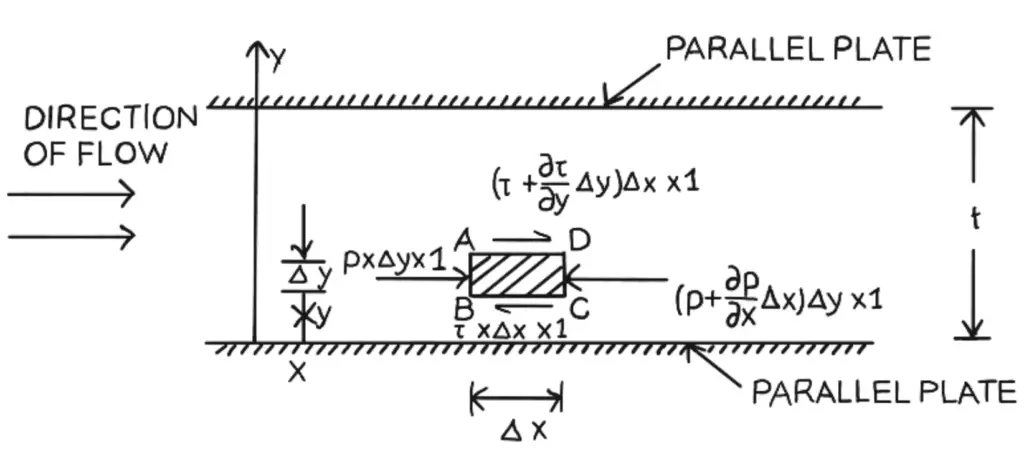
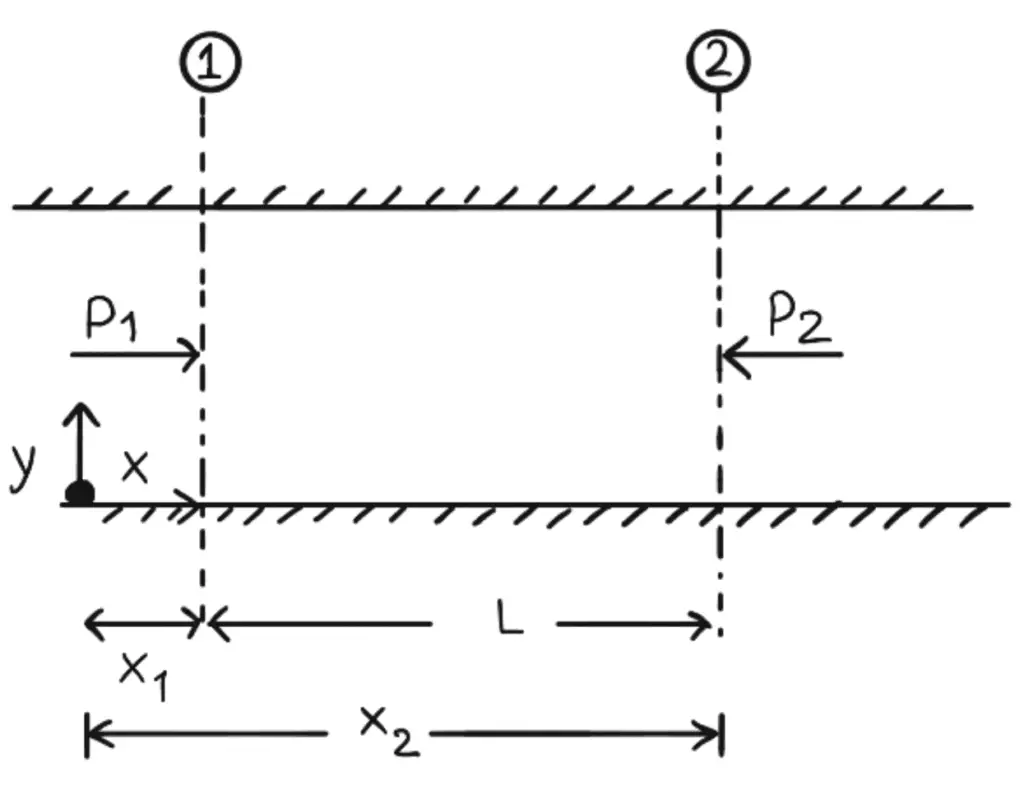
Let us consider two parallel fixed plates kept at a distance ‘t’ apart as shown in the above figure. A viscous fluid is flowing between these two plates from left to right.

Consider a fluid element of length Δx and thickness Δy at a distance y from the lower fixed plate.

If p is the intensity of pressure On the face AB of the fluid element then the intensity of on the face CD will be

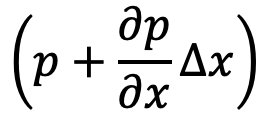
Let 𝜏 be the shear stress acting on the face BC then the shear stress on the face AD Will be

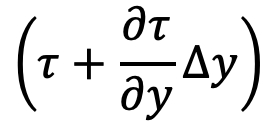
If the width of the element in the direction Perpendicular to the paper is unity then the forces acting on the fluid element are as follows

1. The pressure force on the face AB is p × Δy × 1
2. The pressure force on the face CD will be as follows

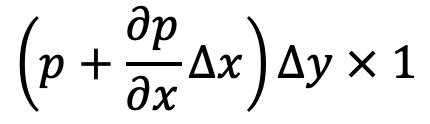
3. The shear force on the face of BC will be 𝜏 × Δx × 1
4. The shear force on the face of AD will be as follows

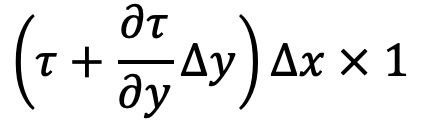
For steady and uniform flow, there is no acceleration and hence the resultant force in the direction of flow is zero.

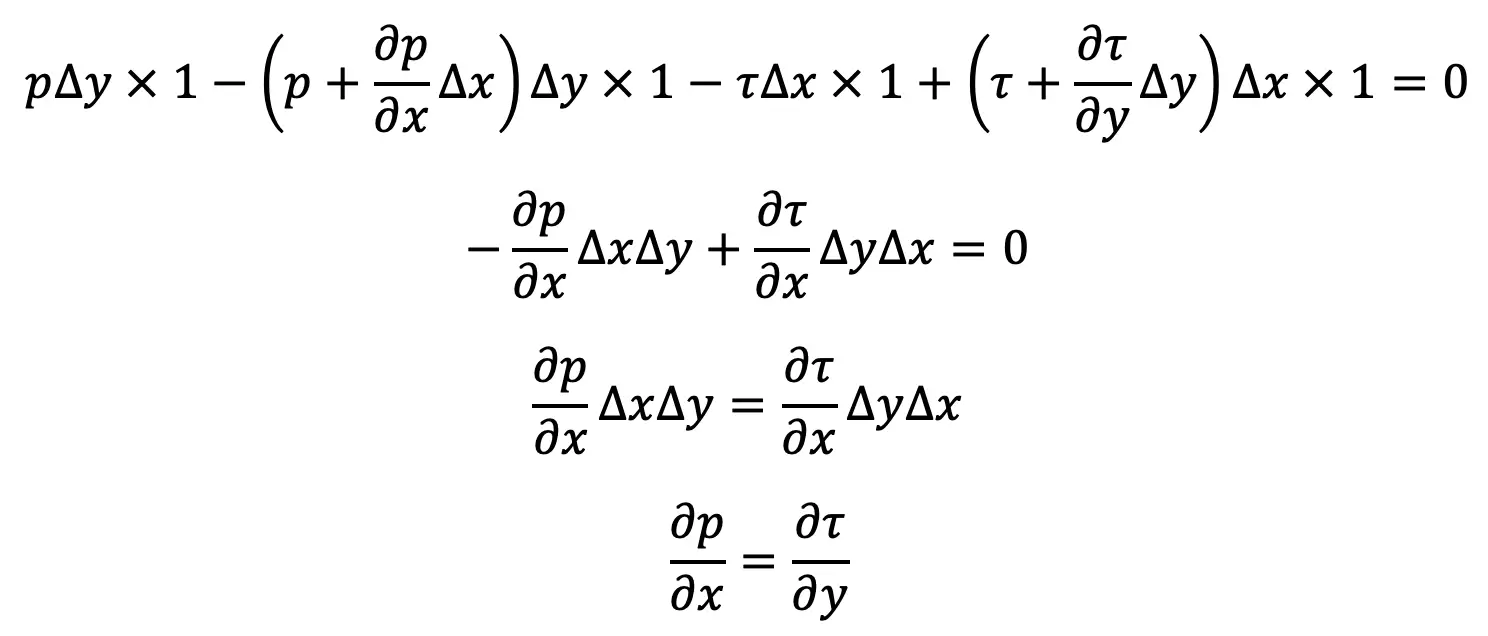
Velocity Distribution Across A Section

To obtain the velocity distribution across a section, the value of shear stress from Newton’s law of viscosity for laminar flow should be submitted into the above equation (a).

We have the shear stress from Newton’s law of viscosity for laminar flow is as follows

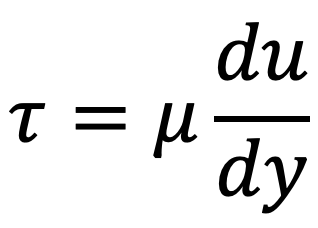
Let us substitute this equation in the above shear stress distribution equation (a), we get

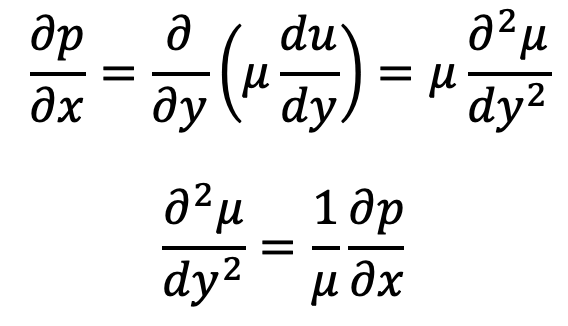
Integrating the above equation 2 times with respect to y on both sides, we get

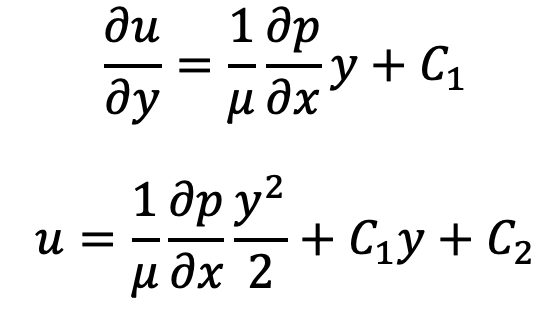
where C₁ and C₂ are constants of integration.

Their values are obtained from the two boundary conditions that are

• at y = 0,u=0
• at y =t, u = 0

Applying the first boundary condition by substituting the values of y=0, and u=0 in equation (b)

0 = 0 + C₁ × 0 + C₂
C₂ = 0

Applying the second boundary condition by substituting the values of y = t, u = 0 in equation (b) gives

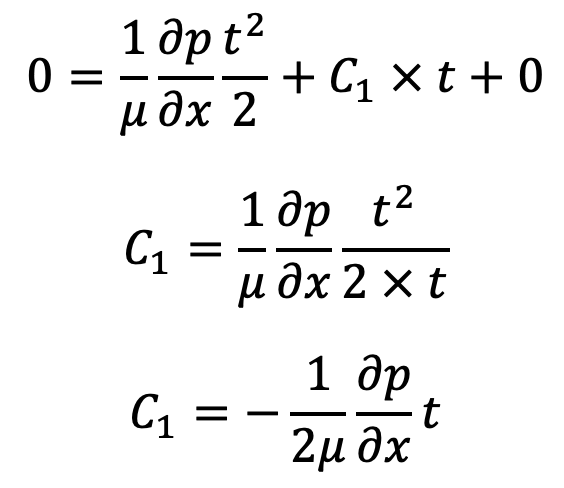
Now, we have the values of C₁ and C₂ by applying the boundary conditions to equation (b), we can Substitute these values of C₁ and C₂ back into equation (b), and we get

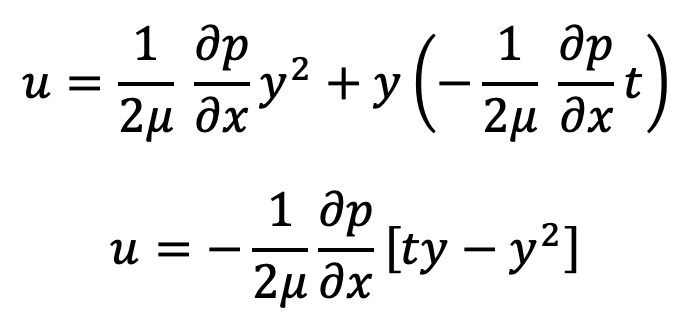
In the above equation, µ, ∂p/∂x and t are constants.

It means u varies with the square of y. Hence equation (c) is an equation of a parabola.

Hence velocity distribution across a section of the parallel plate is parabolic.

This velocity distribution is shown in the following figure.

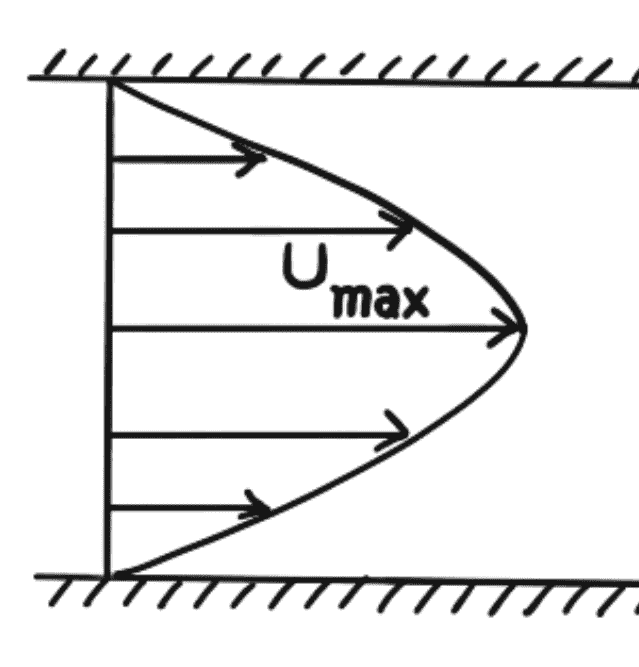
The ratio of Maximum velocity to Average Velocity

The velocity is maximum when y = t/2. We can substitute this value in equation (c) to get the maximum velocity

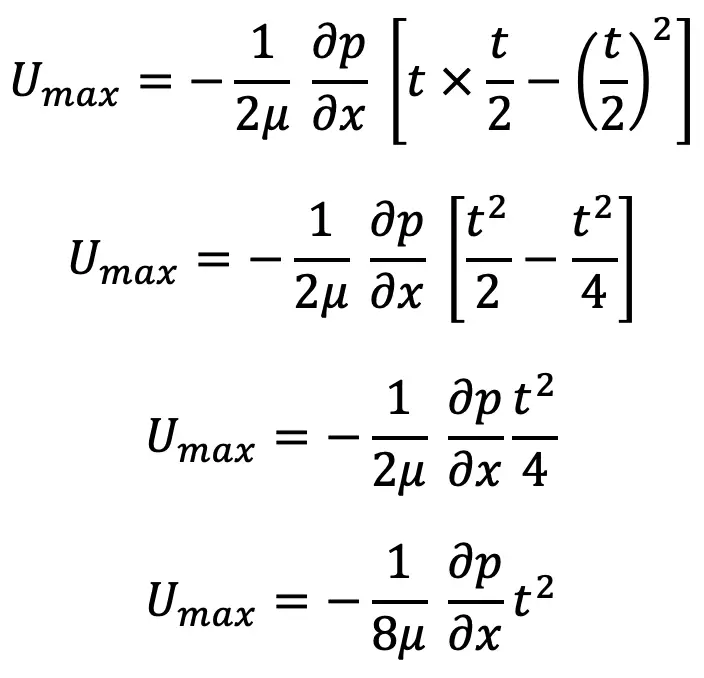
We have the Maximum velocity.

The average velocity can be obtained by dividing the discharge (Q) across the section by the area of the section (t ×1).

And the discharge Q is obtained by considering the rate of flow of fluid through the strip of thickness dy and integrating it.

The rate of now through strip is

dQ = Velocity at a distance y × Area of strip

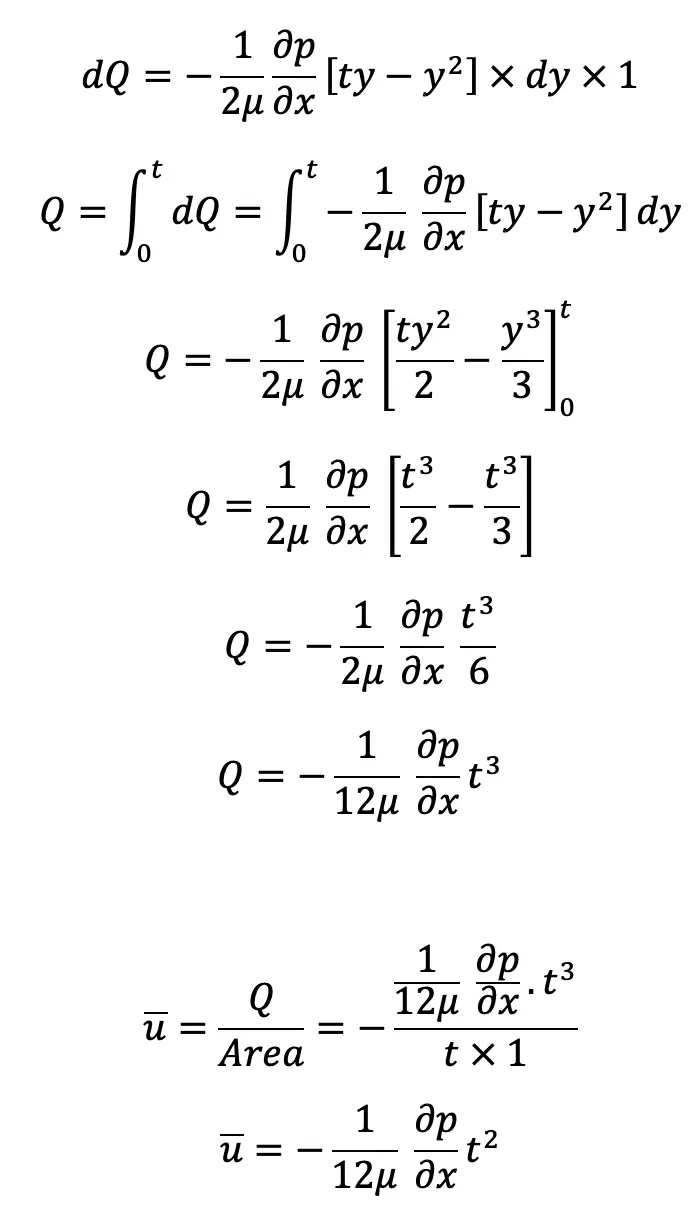
Dividing equation (d) by equation (e), to get the ratio of Maximum velocity to Average Velocity

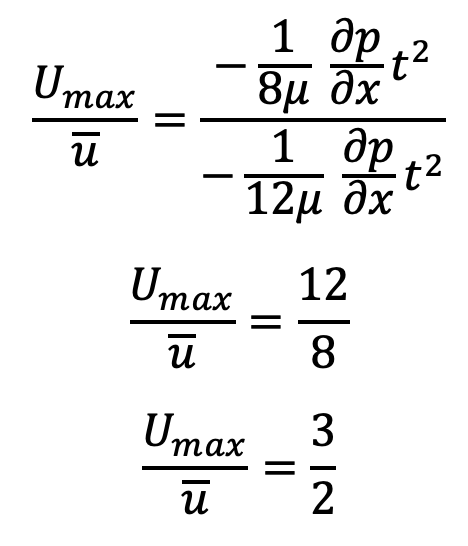
This is the equation for the ratio of Maximum velocity to Average Velocity.

The drop of pressure head for a given Length

From equation (e), we have

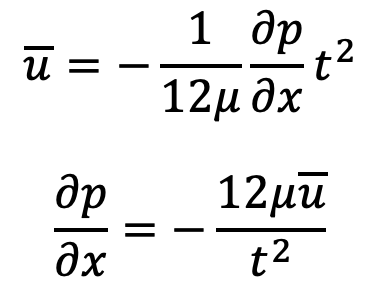
Integrating this equation with respect to x, we get

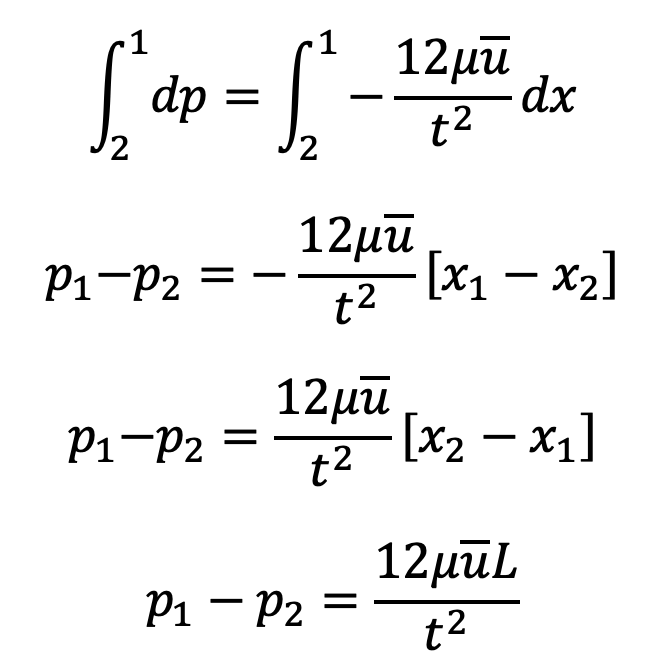
If h_f is the drop of pressure head, then

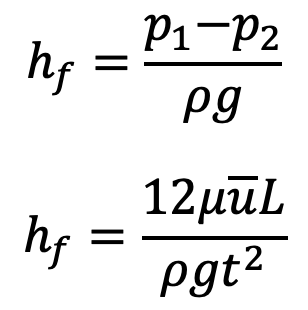
Shear Stress Distribution of Viscous Fluid between two Parallel Plates

Shear Stress Distribution can be obtained by substituting the value of u from equation (a) into

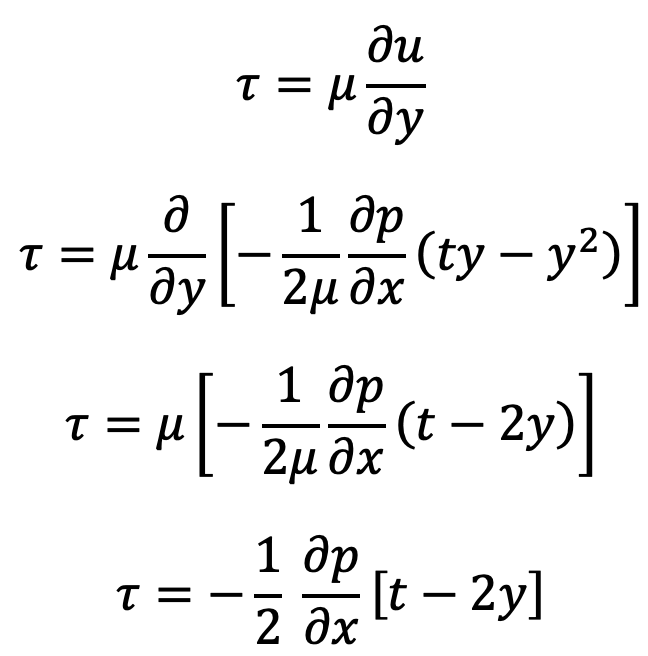
In equation (h), ∂p/∂x and t are constant.

Hence 𝜏 varies linearly with y.

The shear stress distribution is shown in the following figure.

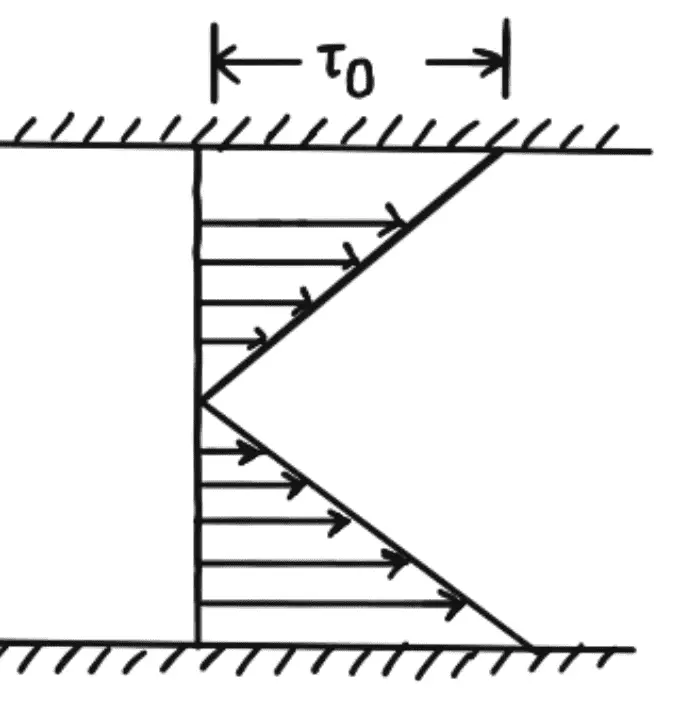
• Shear Stress is maximum when y = 0 or t at the walls of the plates.
• Shear is zero when y = t/2 which is at the centre line between the two plates.

The maximum shear stress (𝜏₀) is given by

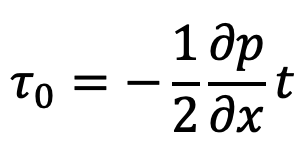
Kinetic Energy Correction And Momentum Correction Factors

Kinetic Energy Correction Factor for Viscous Fluid Flow

The kinetic energy correction factor is defined as the ratio of the kinetic energy of the flow per second based on actual velocity across a section to the kinetic energy of the flow per second based on average velocity across the same section.

It is denoted by α. Hence mathematically,

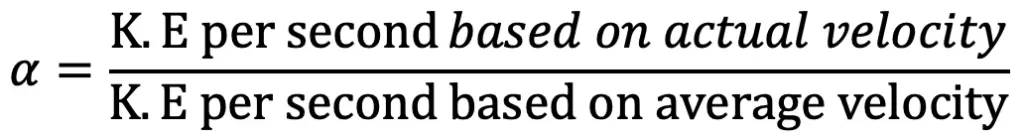
Momentum Correction Factors for Viscous Fluid Flow

Momentum Correction Factor is defined as the ratio of momentum of the flow per second based on actual velocity to the momentum of the flow per second based on average velocity across a section.

It is denoted by β. Hence mathematically

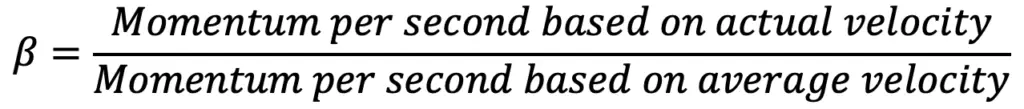
Example Problems on Flow of Viscous Fluid

Let us solve some example Problems to calculate the Pressure Gradient of Viscous fluid and the velocity and the discharge

Problem Statement: The oil of viscosity 0.02 Ns/m² flowing between stationary parallel plates 1 m wide maintained 10 mm apart. The velocity midway between the plates is 2 m/s. Calculate the following
(i) Pressure gradient along the flow
(ii) Average velocity
(iii) Flow Discharge

Answer:

Given data
Viscosity µ = 0.02 Ns/m²
Width b = 1 m
Distance between plates, t = 10 mm = 0.01 m

Velocity midway between the plates, U_max = 2 m/s

(i) Pressure Gradient [dp/dx] Viscous Fluid between two Parallel Plates

Using equation (d) from above

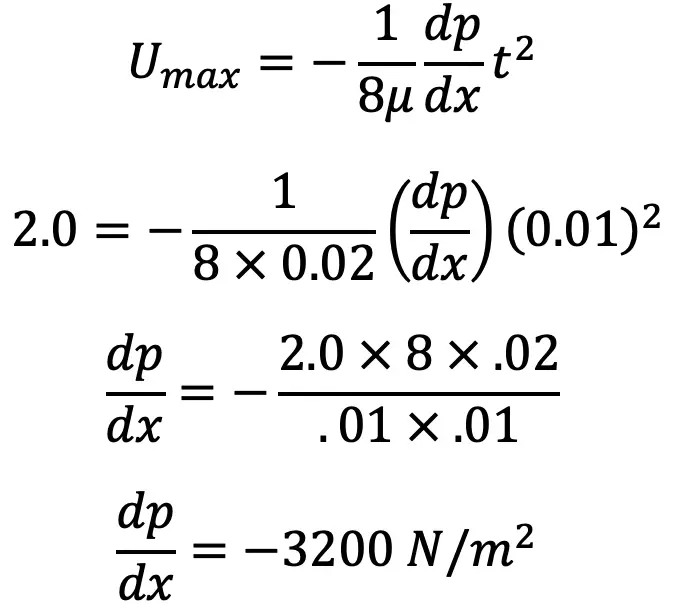
(ii) Average velocity (u) of Viscous Fluid between two Parallel Plates

Using equation (f)

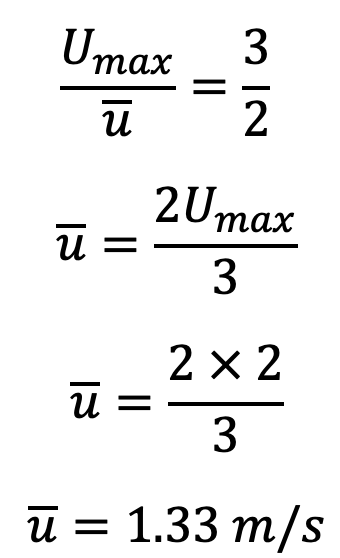
(iii) Discharge (Q) of Viscous Fluid between two Parallel Plates

Q = Area of flow × u
Q = b × t × u
Q = 1 × 0.01 × 1.33
Q = 0.0133 m³/s

This is all about the flow of Viscous Fluid between two Parallel Plates. Let us know what you think about this article in the comment section below.