Stresses in Thick Cylindrical Shell

We have already discussed the different types of pressure vessels previously. The thick cylinder is one of the types of Cylindrical shells which is subjected to very high internal pressures for many applications such as Gun Barrels, Hydraulic cylinders, and pipes. In these applications, the wall thickness must be made thick to accommodate the high internal pressures. In this article, we will discuss how to calculate the stresses in Thick Cylindrical Shell.

In the previous article, we have discussed that the stresses in thin cylindrical walls have assumed that the tensile stresses are uniformly distributed over the section of the walls. But in the case of Thick Cylindrical shells, the stress over the section of the walls cannot be assumed to be uniformly distributed. They develop both tangential and radial stresses with values that are dependent upon the radius of the element under consideration.

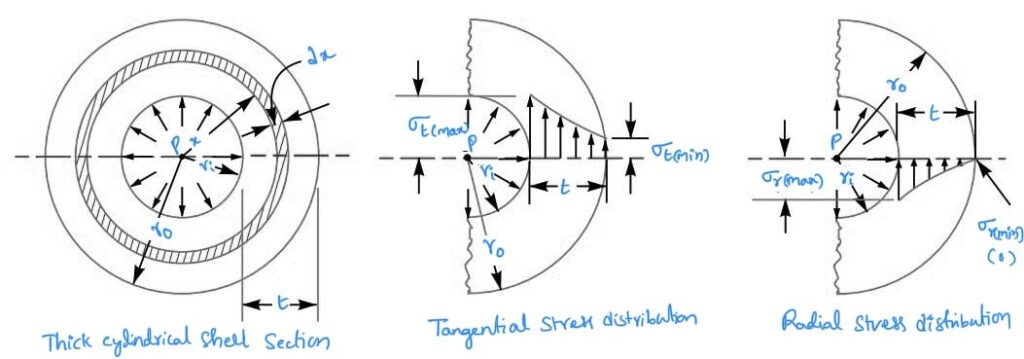
The distribution of stresses in a thick cylindrical shell is shown in the above figure. From the above figure, we see that the tangential stress is maximum at the inner surface and minimum at the shell’s outer surface. The radial stress is maximum at the inner surface and zero at the outer surface of the shell.

To design a thick cylindrical shell for any application such as Gun Barrels, Hydraulic cylinders, and pipes we need to understand few important equations. Those are

1. Lame’s equation
2. Birnie’s equation
3. Clavarino’s equation
4. Barlow’s equation

For the above figure let us assume

r_o = Outer radius of cylindrical shell
r_i = Inner radius of cylindrical shell
t = Thickness of cylindrical shell = r_o – r_i
p = Intensity of internal pressure
μ = Poisson’s ratio
σ_t = Tangential stress
σ_r = Radial stress

Lame’s equation

From Lame’s Theorem, we have two assumptions to make to solve the thick cylinders problems.

1. Material of the Thick cylindrical shell need to be assumed homogeneous and isotropic.
2. Material will be stressed with in the elastic limit and obeys hook’s law
3. Plane sections of the cylinder perpendicular to the longitudinal axis remain plane under the pressure
4. Longitudinal fibres of the cylindrical shell are equally strained

We have lames equation for the tangential stresses at any radius x is given by

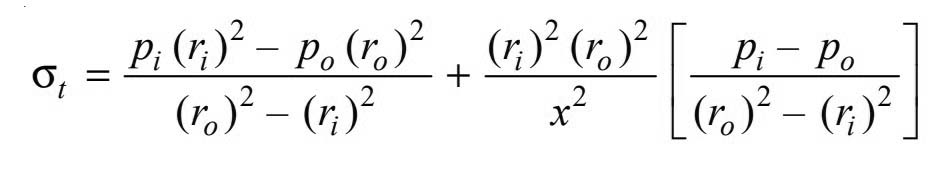
From the lames equation, we have the radial stresses at any radius x

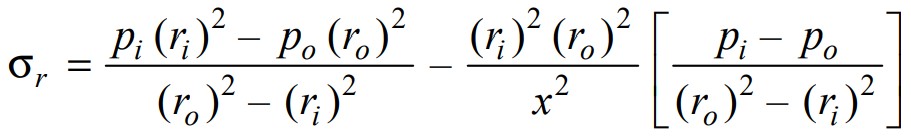
In this article, we are only concerned about the internal pressure, we can substitute the p_o= 0

so we can rewrite the above equations by substituting the p_o= 0 and p_i as simply p

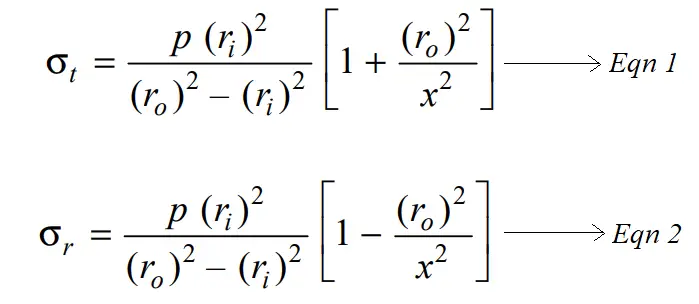
From the schematic diagram of the thick cylindrical section, we can see that the tangential stresses are always tensile, whereas the radial dresses are compressive.

The tangential stress is maximum at the inner surface of the cylinder which is x = r_i and the tangential stress is minimum at the outer surface of the cylinder which is x = r_o

We can rewrite the above Tangential stress equation (Eqn 1) by substituting the above values of x for both maximum and minimum conditions.

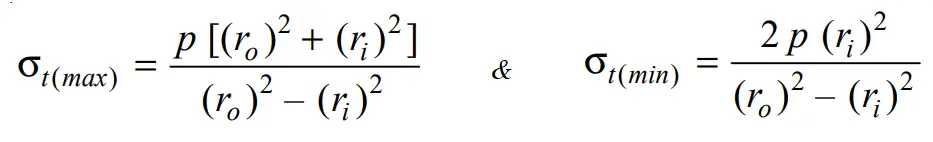
Similarly, The radial stress is maximum at the inner surface of the cylinder which is x = r_i and the radial stress is zero at the outer surface of the cylinder which is x = r_o

We can rewrite the above Radial stress equation (Eqn 2) by substituting the above values of x for both maximum and minimum conditions.

σ_r(max) = – p (compressive)

σ_r(min) = 0

To design a thick cylindrical shell from brittle materials such as cast iron, hard steel and cast aluminium, with an open-end or closed-end shell, we need to design per the maximum normal stress theory failure.

The tangential stress can be written as

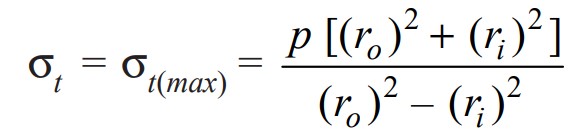
We know the wall thickness is t = r_o – r_i

From this, we can write r_o = r_i + t

We can substitute this in the above equation. we get

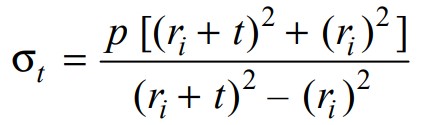
And further simplified

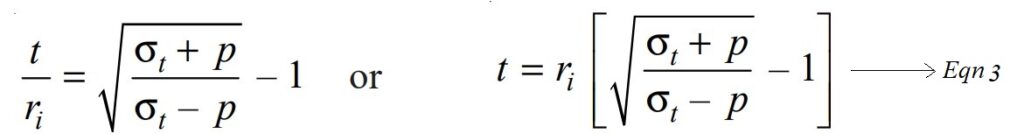
This is the equation for the design of a thick cylindrical shell for brittle materials only. The value of σ_t for brittle materials may be taken as 0.125 times the ultimate tensile strength (σ_u). For the Ductile materials, the design of the thick cylindrical shell the Lame’s equation is modified according to the maximum shear stress theory.

According to this Maximum shear stress theory, the maximum shear stress at any point is equal to one half of the algebraic difference of the maximum and minimum principal stresses at that point.

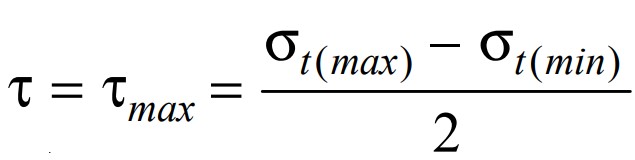
The maximum principle at the inner surface is

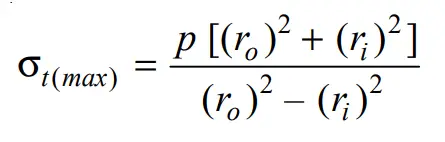
and minimum principal stress at the outer surface is

σ_t(min) = – p

We can substitute these in the following Maximum shear stress equation. also, substitute r_o = r_i + t

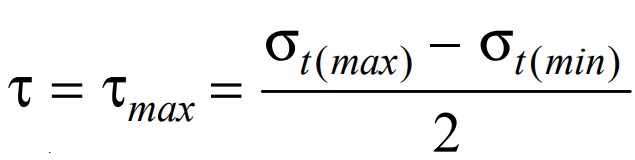
We get finally

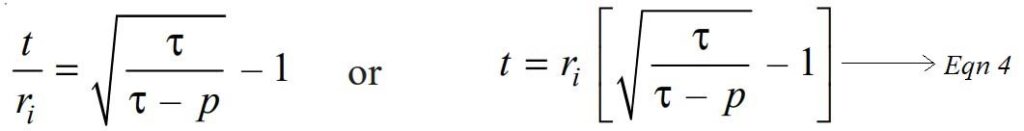
The value of shear stress (τ) is usually taken as one-half the tensile stress (σ_t).

Therefore the above expression may be written as follows

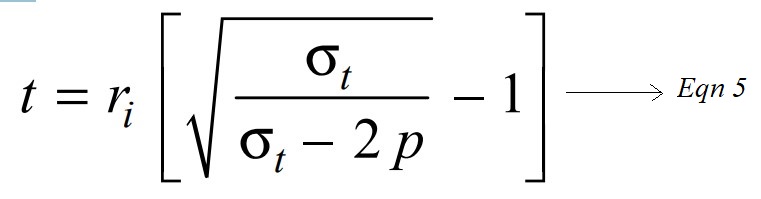
As we can see that from the above equation the p (internal pressure) in the denominator can not be equal or greater than the allowable working stress (σ_t or τ). If p is equal to or greater than the allowable working stress (σ_t or τ), then no thickness of the cylinder wall will prevent failure.

Thus, it is impossible to design a cylinder to withstand fluid pressure greater than the allowable working stress for a given material.

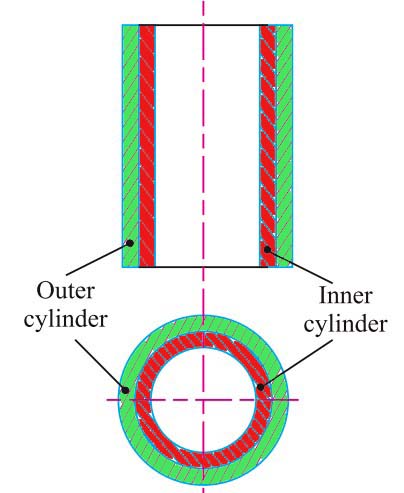
To overcome this difficulty, we use compound cylinders design. Following is a schematic diagram of a compound cylinder how it looks like.

Birnie’s equation

In the case of open-end cylinders such as pump cylinders, rams, gun barrels etc. made of ductile material, for example, low carbon steel, brass, bronze, and aluminium alloys, the allowable stresses cannot be determined using the maximum-stress theory of failure. In such cases, the maximum-strain theory is used. According to this theory, the failure occurs when the strain reaches a limiting value and Birnie’s equation for the wall thickness of a cylinder is

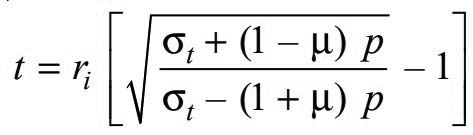
The value of Maximum stresses σ_t may be taken as 0.8 times the yield point stress (σ_y).

Clavarino’s equation

This equation is also based on the maximum-strain theory of failure, but it is applied to closed-end cylinders (or cylinders fitted with heads) made of ductile material. According to this equation, the thickness of a cylinder,

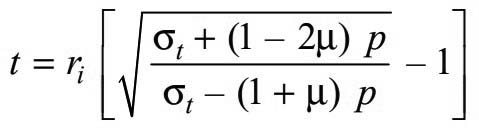
In this case, also, the value of Maximum stresses σ_t may be taken as 0.8 times the yield point stress (σ_y).

Barlow’s equation

This equation is generally used for high-pressure oil and gas pipes. According to this equation, the thickness of a cylinder,
t = p.r_o / σ_t

In this case, also, the value of Maximum stresses σt may be taken as 0.8 times the yield point stress (σy) for the ductile materials. But for the brittle materials, Maximum stresses σt may be taken as 0.125 times the ultimate tensile strength (σu) which is similar to the Lames, equation.

Conclusion

We have discussed how we can find the stresses in the thick cylindrical shell by discussing 4 different equations for different cylinders such as open-end and closed-end, also for the different materials such as the brittle and ductile material. Let us know what do you think about these equations to find the thickness of a cylinder for your application.