Stresses in a Thin Cylindrical Shell

You must have seen heavy vehicles transporting fluids such as water/petroleum or steam boilers in some industrial plants etc. with a cylindrical structure called tanks or Pressure vessels. These Pressure vessels are used to store the fluids under the pressure. Since these fluids are stored under pressure, these may undergo a state of change inside the pressure vessel. There should be a very high amount of care that should be taken while designing a pressure Vessel. A rupture of a pressure vessel means an explosion that may lead to loss of property or even many lives. In this article, we are going to discuss the different Stresses in a Thin Cylindrical Shell due to Internal Pressure.

As we have discussed the different types of Pressure vessels in the previous article based on internal pressure and allowable stress. Let us discuss the stresses in a Thin cylindrical shell due to internal pressure.

Assumptions made for analysing the Stresses in a Thin Cylindrical Shell

Based on the following assumptions that we made, we can analyze the stresses induced in a thin cylindrical shell.

1. The influence of cylinder wall curvature is neglected.
2. The tensile stresses are uniformly distributed over the section of the walls.
3. The influence of the restraining action of the heads at the end of the pressure vessel is neglected.

Now with the above assumptions, if a thin cylindrical shell is subjected to internal pressure, then the shell most likely fail in the following two ways.

1. It may fail along the longitudinal section (i.e. circumferentially) splitting the cylinder into two troughs, as shown in the below picture

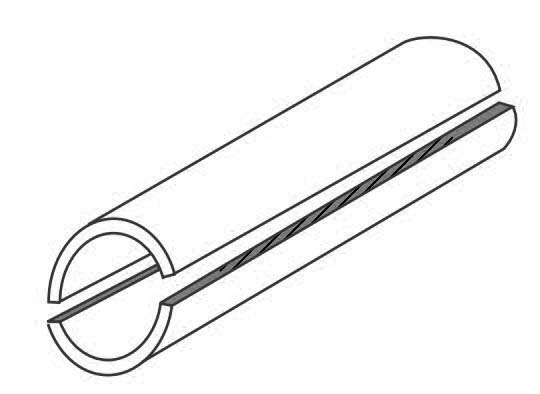
2. It may fail across the transverse section (i.e. longitudinally) splitting the cylinder into two cylindrical shells, as shown in the below picture

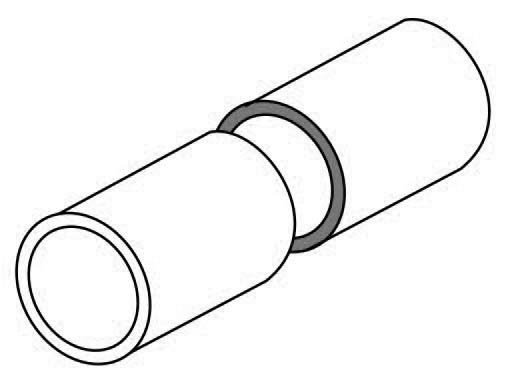
Thus the wall of the cylindrical shell subjected to an internal pressure has to withstand tensile stresses of the following two types:

• Circumferential or hoop stress
• Longitudinal stress.

Let us discuss these two kinds of Stresses in a Thin Cylindrical Shell due to Internal Pressure.

Circumferential or hoop stress

Let us Consider a thin cylindrical shell subjected to internal pressure and A tensile stress acting in a direction tangential to the circumference is called circumferential or hoop stress. In other words, it is tensile stress on the longitudinal section (or on the cylindrical walls).

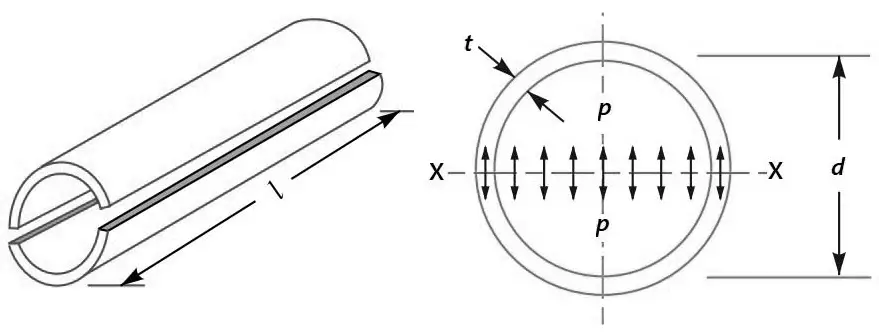
Where,
p = Intensity of internal pressure
d = Internal diameter of the cylindrical shell
l = Length of the cylindrical shell
t = Thickness of the cylindrical shell
σ_t1 = Circumferential or hoop stress for the material of the cylindrical shell.

We know that the total force acting on a longitudinal section which is along the diameter X-X of the shell
= Intensity of pressure × Projected area = p × d × l …….. (a)

The total resisting force acting on the cylinder walls
= σ_t1 × 2t × l …( of two sections) ……(b)

From the above equations (a) & (b) we can equate them

σ_t1 × 2t × l = p × d × l

σ_t1 = (p × d)/2t ……(c)

From equation (c) we can obtain the Circumferential or hoop stress for the cylindrical shell when the intensity of the pressure inside the shell is known and the thickness and the diameter of the shell are known.

or we can write the equation (c) in terms of thickness.

t = (p × d)/σ_t1 …..(d)

Check how to calculate Hoop stress here!

Things to be noted while designing cylindrical shells for Specific applications

1. In the design of engine cylinders, a value of 6 mm to 12 mm is added in equation (d) to permit reboring after wear has taken place. Therefore 6 or 12 need to be added to the equation (d). i.e. t =( (p × d)/σ_t1 )+ 6 to 12mm
2. In constructing large pressure vessels like steam boilers, riveted joints or welded joints are used in joining together the ends of steel plates. In case of riveted joints, the wall thickness of the cylinder will be t = (p × d)/(σ_t1×η_l) where η_l is the Efficiency of the longitudinal riveted joint.
3. In case of cylinders of ductile material, the value of circumferential stress (σ_t1) may be taken 0.8 times the yield point stress (σ_y) and for brittle materials, σ_t1 may be taken as 0.125 times the ultimate tensile stress (σ_u).
4. In designing steam boilers, the wall thickness calculated by the above equation may be compared with the minimum plate thickness as provided in boiler code as given in the following table.

Boiler diameter	Minimum plate thickness (t)
0.9 m or less	6 mm
Above 0.9 m and up to 1.35 m	7.5 mm
Above 1.35 m and up to 1.8 m	9 mm
Over 1.8 m	12 mm

The boiler code also provides that the factor of safety shall be at least 5 and the steel of the plates and rivets shall have as a minimum the following ultimate stresses.
Tensile stress, σ_t = 385 MPa
Compressive stress, σ_c = 665 MPa
Shear stress, τ = 308 MPa

Longitudinal Stress

Let us Consider a closed thin cylindrical shell subjected to internal pressure as shown below figure. Tensile stress acting in the direction of the axis is called longitudinal stress. In other words, it is tensile stress acting on the transverse or circumferential section Y-Y or on the ends of the vessel.

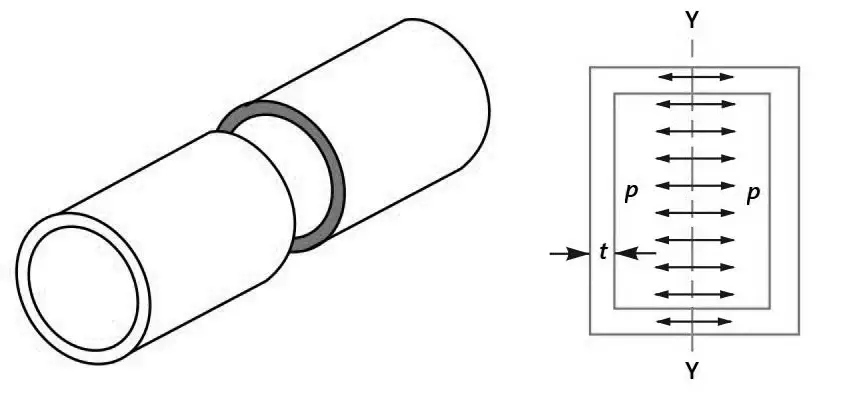
σ_t2 = Longitudinal stress

In this case, the total force acting on the transverse section which is along Y-Y
= Intensity of pressure (p)× Cross-sectional area (πd²/4) = p × πd²/4 …..(e)

The total resisting force is = σ_t2 × π d.t …..(f)

From the above equations (e) & (f), we can equate them.

σ_t2 × π d.t = p × πd²/4

σ_t2 = p×d/4t …..(g)

From equation (g) we can obtain the Longitudinal Stress for the cylindrical shell when the intensity of the pressure inside the shell is known and the thickness and the diameter of the shell are known.

or we can write the equation (g) in terms of thickness.

t = p×d/4σ_t2 …..(h)

Conclusion

From the above equations, we understood that the Longitudinal Stresses are half the Circumferential or hoop stress. Therefore the design of a pressure vessel must be based on the maximum stress that is hoop stresses.

Exercise

Problem Statement: A thin cylindrical pressure vessel of 1.2 m diameter generates steam at a pressure of 1.75 N/mm2. Find the minimum wall thickness, if (a) the longitudinal stress does not exceed 28 MPa; and (b) the circumferential stress does not exceed 42 MPa.

Please solve the above problem and let us know the answer in the comment section below. I will help you with the answers.