How to calculate Hoop Stresses?

In the previous article, we have discussed stresses in a thin cylinder, we have discussed that the wall of the cylindrical shell subjected to internal pressure due to the fluid has to withstand two types of tensile stresses. Those are Circumferential stress or hoop stress and longitudinal stress. In this article let us see how we can calculate the Hoop Stresses for any given cylinder with internal pressure.

Hoop stress or Circumferential stress

The internal or external pressure applied to thin cylinders is resisted by stresses developed in the
circumferential direction of the cylinder. This type of stress is called hoop stress.

In other words, the tensile stress on the longitudinal section or on the cylindrical walls is the hoop stress. Following is an example picture to represent the failure caused in pipes due to the hoop stresses.

Let us Consider a thin cylindrical shell subjected to internal pressure p.

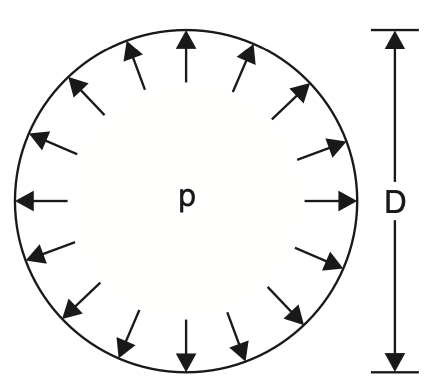
where
p = Intensity of internal pressure
D = Internal diameter of the cylindrical shell
t = Thickness of the cylindrical shell
f = Circumferential or hoop stress for the material of the cylindrical shell.

following assumptions that we made, to analyze the hoop stresses induced in the thin cylinders.

1. The influence of cylinder wall curvature is neglected.
2. The tensile stresses are uniformly distributed over the section of the walls.
3. The influence of the restraining action of the heads at the end of the pressure vessel is neglected.

Consider half the section as shown below figure.

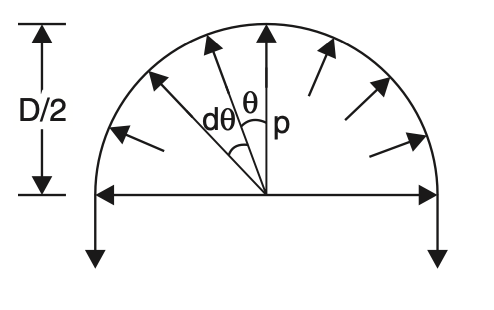
The normal pressure on the element of unit length as shown in the above figure is given by

= p × (D/2) × dθ

Its vertical component = pD /2 dθ cos θ

Bursting force normal to the horizontal section will be

= 2∫₀^π/2cosθ dθ
= pD [sinθ]₀^π/2
= pD

This bursting force is resisted by the hoop stresses f.

Let ‘t’ be the thickness of the cylinder. Then resisting force per unit length of the cylinder will be
= 2 × ft

Equating resisting force to bursting force, we will get the following relation
2ft = pD
f = pD/2t

Let us solve an example problem to calculate Hoop stresses

Example Problem to Calculate Hoop Stresses

A thin cylinder of internal diameter D = 1 m and thickness t = 12 mm is subjected to the internal pressure of 2 N/mm². calculate the hoop stress developed in the cylinder.

Answer:

Given that the cylinder internal diameter D = 1m = 1000mm

Thickness of the Cylinder t = 12mm

Internal pressure p = 2 N/mm²

We know from the above relation for Hoop stress f = pD /2t
f = (2×1000)/(2× 12)
f = 83.33 N/mm²

The hoop stresses developed inside the cylinder are 83.33 N/mm².