A spring is defined as an elastic body, whose function is to distort when loaded and to recover its original shape when the load is removed. It absorbs or controls energy due to either shock or vibration so it can be used as shock absorbers and vibration dampers. It is also used to apply forces, as in brakes, clutches, and spring-loaded valves. We have already discussed different types of springs in the previous article. Let us discuss the Springs in Series, Parallel, and Concentric, or Composite Springs.

Applications of Springs
The various important applications of springs are as follows:
- To cushion, absorb, or control energy due to either shock or vibration as in car springs, railway buffers, aircraft landing gears, shock absorbers, and vibration dampers.
- To apply forces, as in brakes, clutches, and spring-loaded valves.
- To control motion by maintaining contact between two elements as in cams and followers.
- To measure forces, as in spring balances and engine indicators.
- To store energy, as in watches, toys, etc.
Types of Springs
Though there are many types of springs, the following, according to their shape, are important from the subject point of view.
- Helical springs
- Conical and volute springs
- Torsion springs
- Laminated or leaf springs
- Disc or Belleville springs
- Special-purpose springs
We have discussed more details in a separate article here!
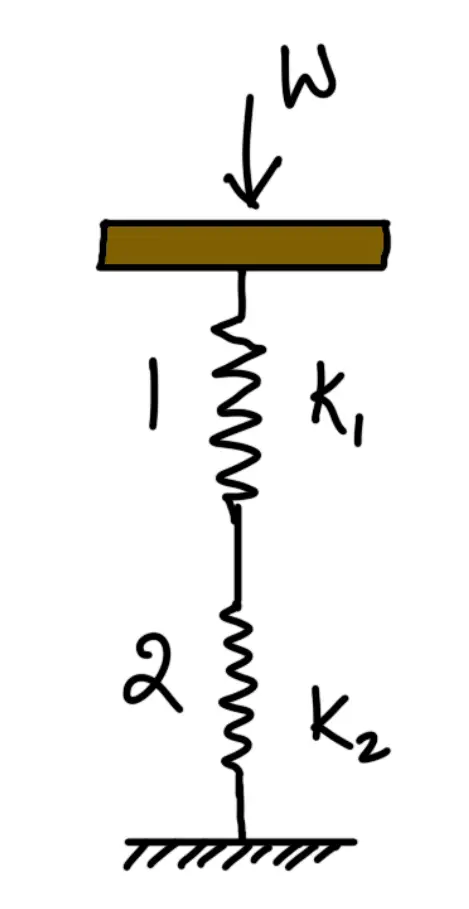
Springs in Series
Consider two springs connected in series as shown in the following figure.
Let
W = Load carried by the springs
δ1 = Deflection of spring 1
δ2 = Deflection of spring 2
k1 = Stiffness of spring 1 = W / δ1
k2 = Stiffness of spring 2 = W/δ2
A little consideration will show that when the springs are connected in series, then the total deflection produced by the springs is equal to the sum of the deflections of the individual springs.
∴ Total deflection of the springs δ = δ1 + δ2
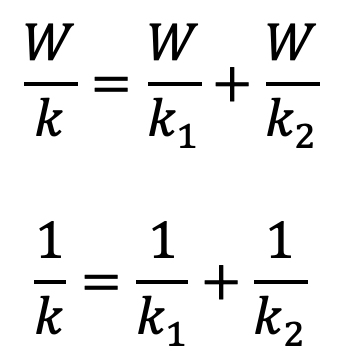
where
k = Combined stiffness of the springs
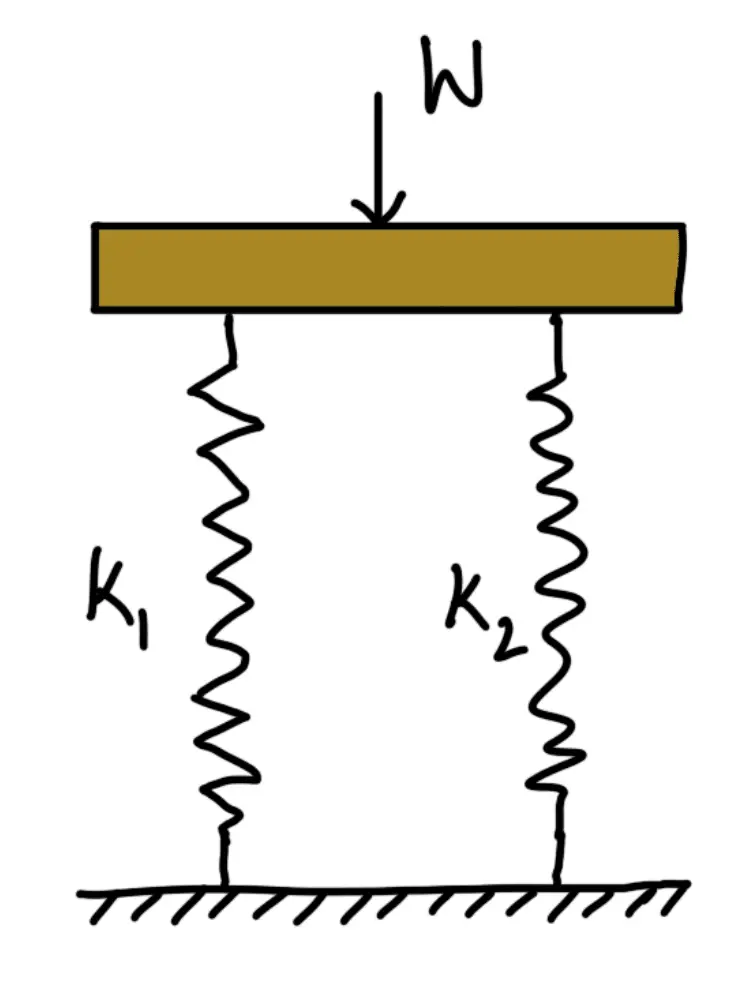
Springs in Parallel
Consider two springs connected in parallel as shown in the following figure.
Let
W = Load carried by the springs
W1 = Load shared by spring 1
W2 = Load shared by spring 2
k1 = Stiffness of spring 1
k2 = Stiffness of spring 2
A little consideration will show that when the springs are connected in parallel, then the total deflection produced by the springs is the same as the deflection of the individual springs.
We know that W = W1 + W2
δ.k = δ.k1 + δ.k2
k = k1 + k2
Where
k = Combined stiffness of the springs
δ = Deflection produced
Example problems on Springs in Series and Parallel
Let us solve an Example problem to find the stiffness of springs in Series and Parallel.
Problem Statement: A close-coiled helical compression spring of 12 active coils has a spring stiffness of k. It is cut into two springs having 5 and 7 turns. Determine the spring stiffnesses of resulting springs.
Answer:
Given data:
Total number of coils of springs n = 12
First spring number of coils n1 = 5
Second spring number of coils n2 = 7
We know that the deflection of the spring
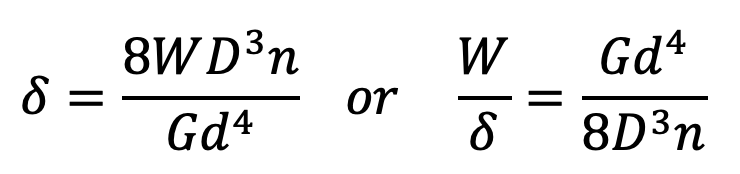
Since G, D, and d are constant, therefore substituting
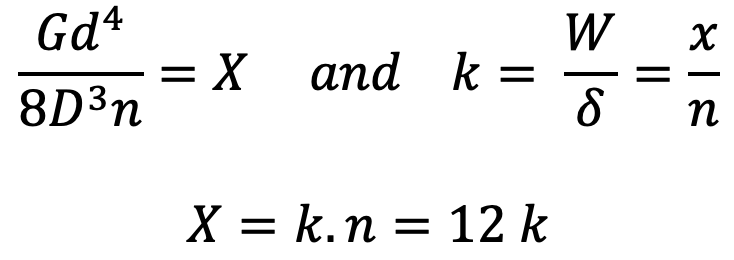
The spring is cut into two springs with n1 = 5 and n2 = 7
Let
k1 = Stiffness of spring having 5 turns
k2 = Stiffness of spring having 7 turns
The Stiffness of spring having 5 turns is
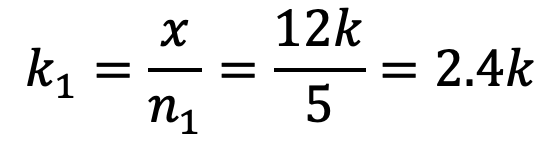
The Stiffness of spring having 7 turns
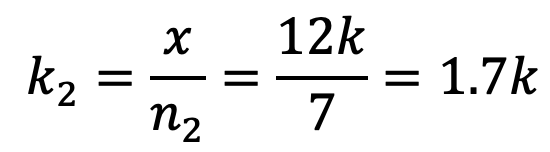
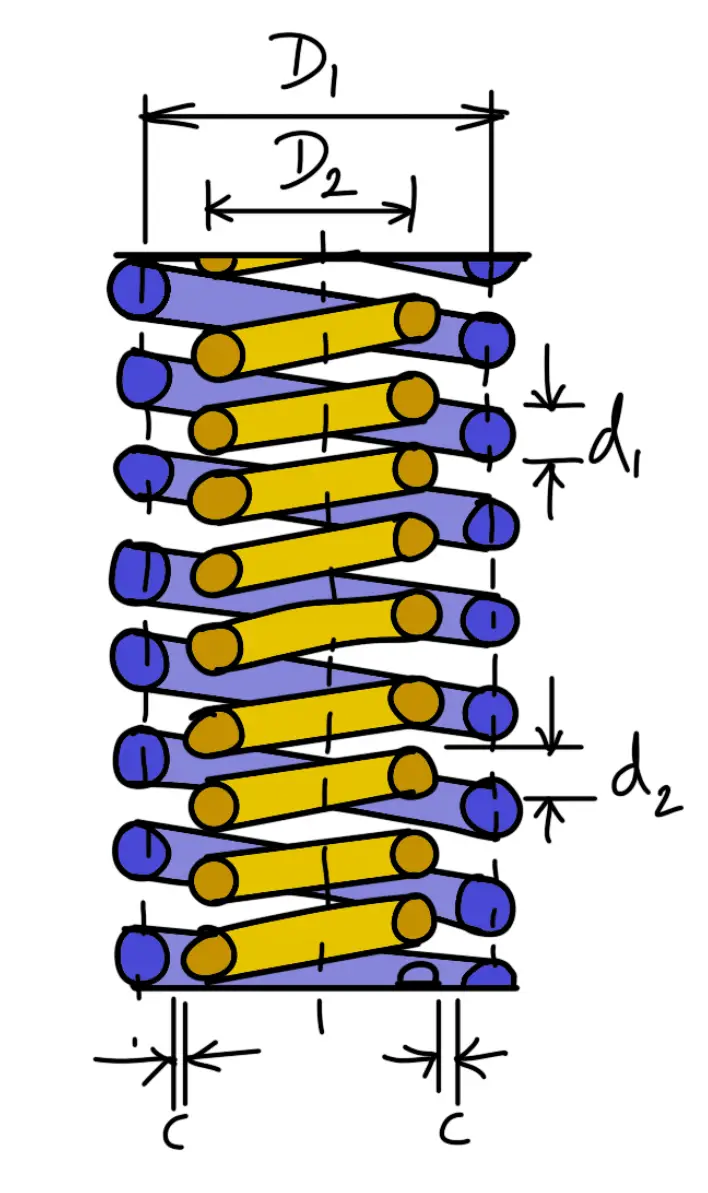
Springs in Concentric, or Composite Springs
A concentric or composite spring is used for one of the following purposes:
- To obtain greater spring force within a given space.
- To ensure the operation of a mechanism in the event of failure of one of the springs.
The concentric springs for the above two purposes may have two or more springs and have the same free lengths as shown in the following figure and are compressed equally. Such springs are used in automobile clutches, valve springs in aircraft, heavy-duty diesel engines, and rail-road car suspension systems.
Sometimes concentric springs are used to obtain a spring force which does not increase in a direct relation to the deflection but increases faster. Such springs are made of different lengths as shown in the following figure. The shorter spring begins to act only after the longer spring is compressed to a certain amount. These springs are used in governors of variable-speed engines to take care of the variable centrifugal force.
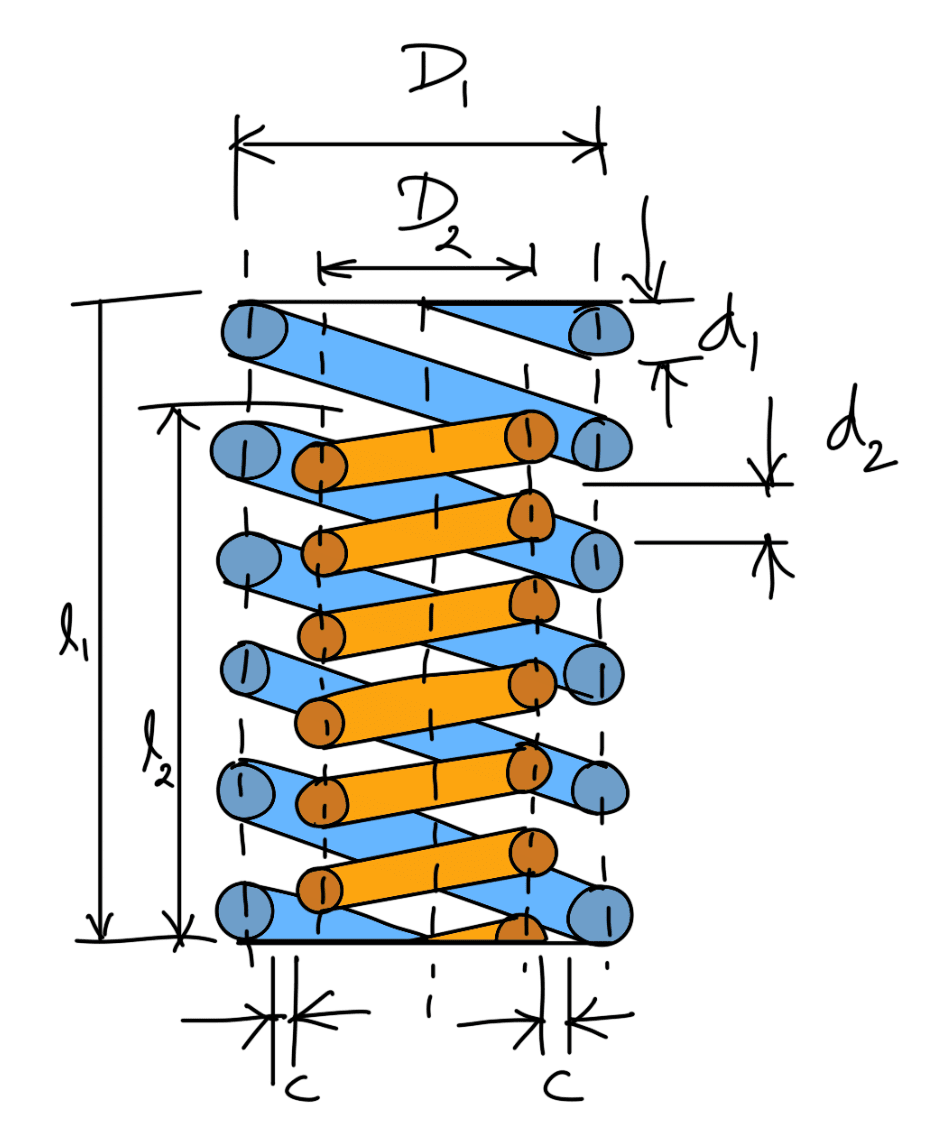
The adjacent coils of the concentric spring are wound in opposite directions to eliminate any tendency to bind.
If the same material is used, the concentric springs are designed for the same stress. In order to get the same stress factor (K), it is desirable to have the same spring index (C).
Consider a concentric spring as shown in above first schematic figure.
Let
W = Axial load
W1 = Load shared by outer spring
W2 = Load shared by innerspring
d1 = Diameter of spring wire of outer spring
d2 = Diameter of spring wire of innerspring
D1 = Mean diameter of outer spring
D2 = Mean diameter of innerspring
δ1 = Deflection of outer spring
δ2 = Deflection of innerspring
n1 = Number of active turns of outer spring
n2 = Number of active turns of innerspring
Assuming that both the springs are made of the same material, then the maximum shear stress induced in both the springs is approximately the same, i.e.
τ1 = τ2
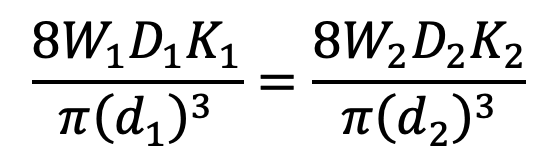
When stress factor, K1 = K2, then
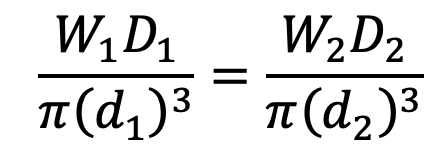
….. Equation (1)
If both the springs are effective throughout their working range, then their free length and deflection are equal, i.e. δ1 = δ2
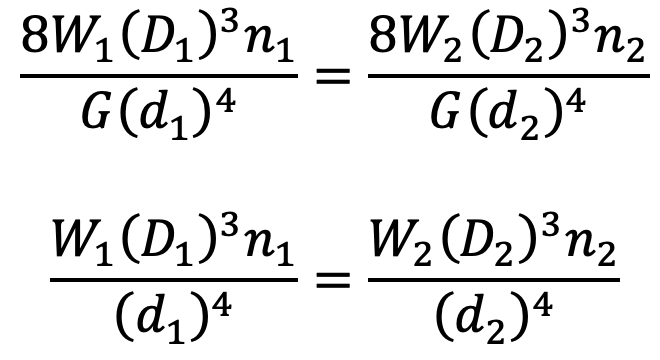
….. Equation (2)
When both the springs are compressed until the adjacent coils meet, then the solid length of both springs is equal, i.e.
n1. d1 = n2.d2
∴ The above equation (2) may be written as
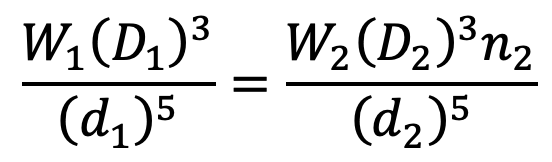
….. Equation (3)
Now dividing equation (3) by equation (1), we have
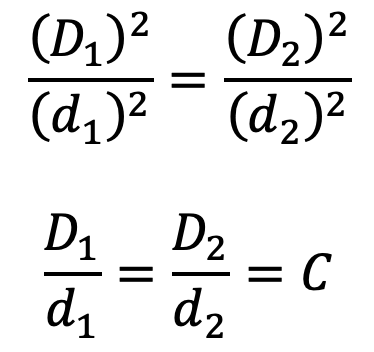
….. Equation (4)
i.e. the springs should be designed in such a way that the spring index for both the springs is same.
From equations (1) and (4), we have
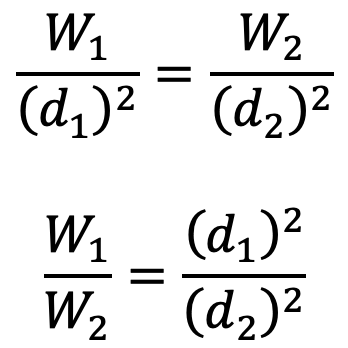
….. Equation (5)
From the above figure, we find that the radial clearance between the two springs,
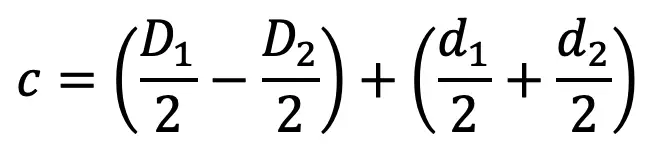
Usually, the radial clearance between the two springs is taken as (d1 – d2) / 2
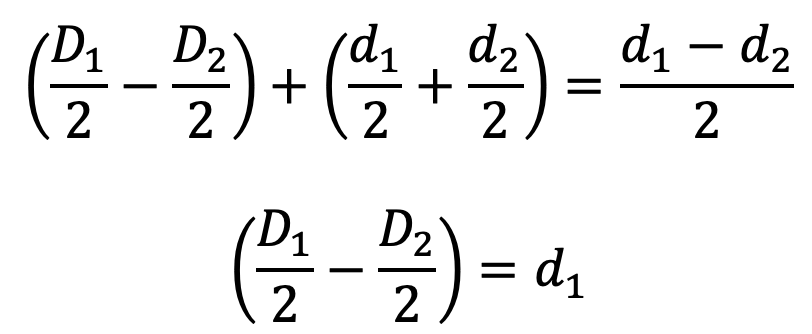
From equation (4), we find that
D1 = C.d1, and D2 = C.d2
Substituting the values of D1 and D2 in equation (4), we have
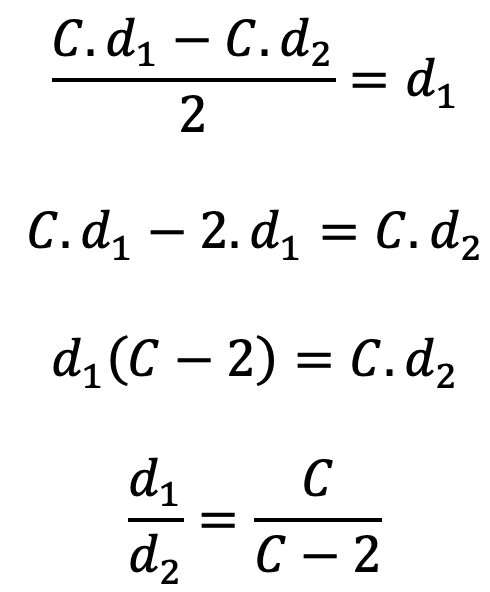
This is all about the Springs in Series, Parallel and Concentric. Let us know what you think about this article in the comment section below.

Leave a Reply