From all the way, we have discussed the different types of stress and strains, Now its time to understand what are the principal stresses. The maximum stress induced in a plane is called the principal stress and the plane at which the maximum stress induced referred to the principal plane where the shear stress is considered zero. Make sense to you? let’s discuss briefly.

Principal Stresses and Principal Planes

A stress is a perpendicular force acting on an object per unit area. In every object, there are three planes which are mutually perpendicular to each other. These will carry the direct stress only no shear stress. Out of these three direct stresses, there will be one maximum stress and one minimum stress among these planes.

The maximum stress is called the Principal stress and the plane at which the maximum stress induced is called the Principal plane and the shear stress will be zero on the principal planes.

Question: how the shear stress will be zero in Principal planes?

Let’s see how a normal stress and the shear stress will be induced in the different load applying conditions.

Case i: 

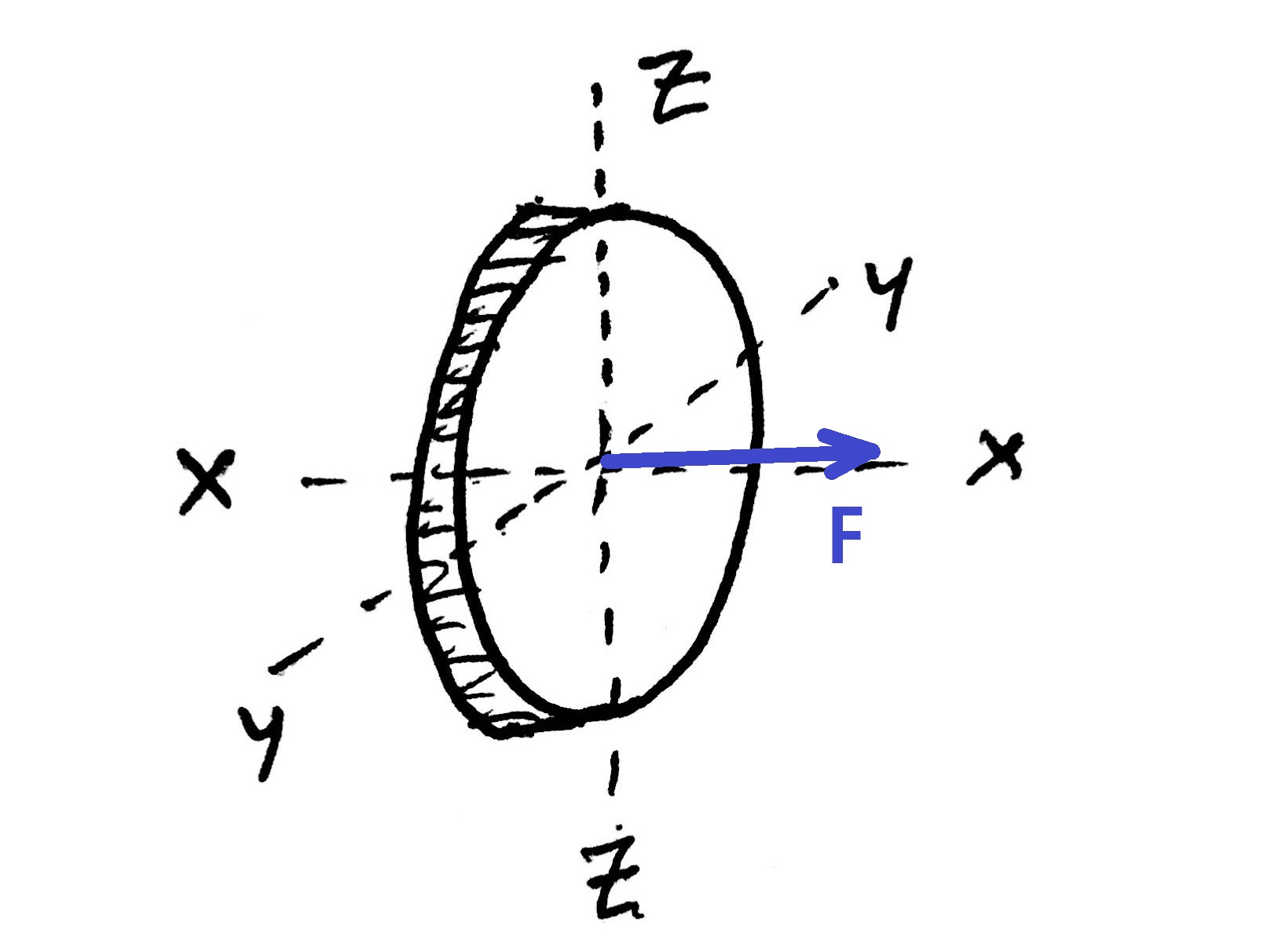
Consider a circular disc with a unit thickness as shown in the above fig.

When a force is applied normal(Along X-axis) to the surface area of the disc as shown then there will be normal stress on the YZ plane. There will be no shear stresses.

Case ii:

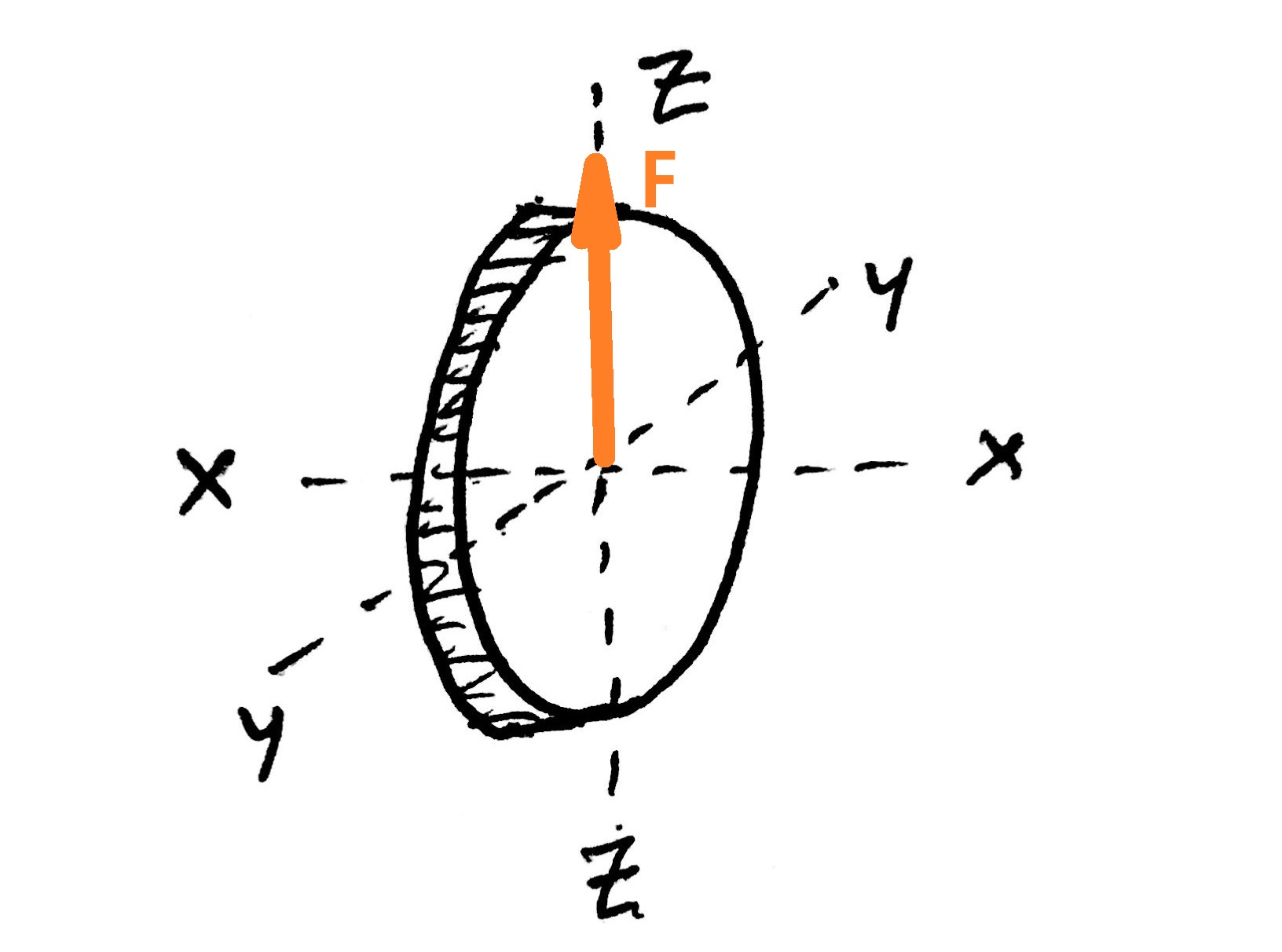
When a force is applied tangentially to the disc surface (along Z-axis) then there will be shear stress induced in the layers of the disc. there is no normal stress will be induced.

Case iii:

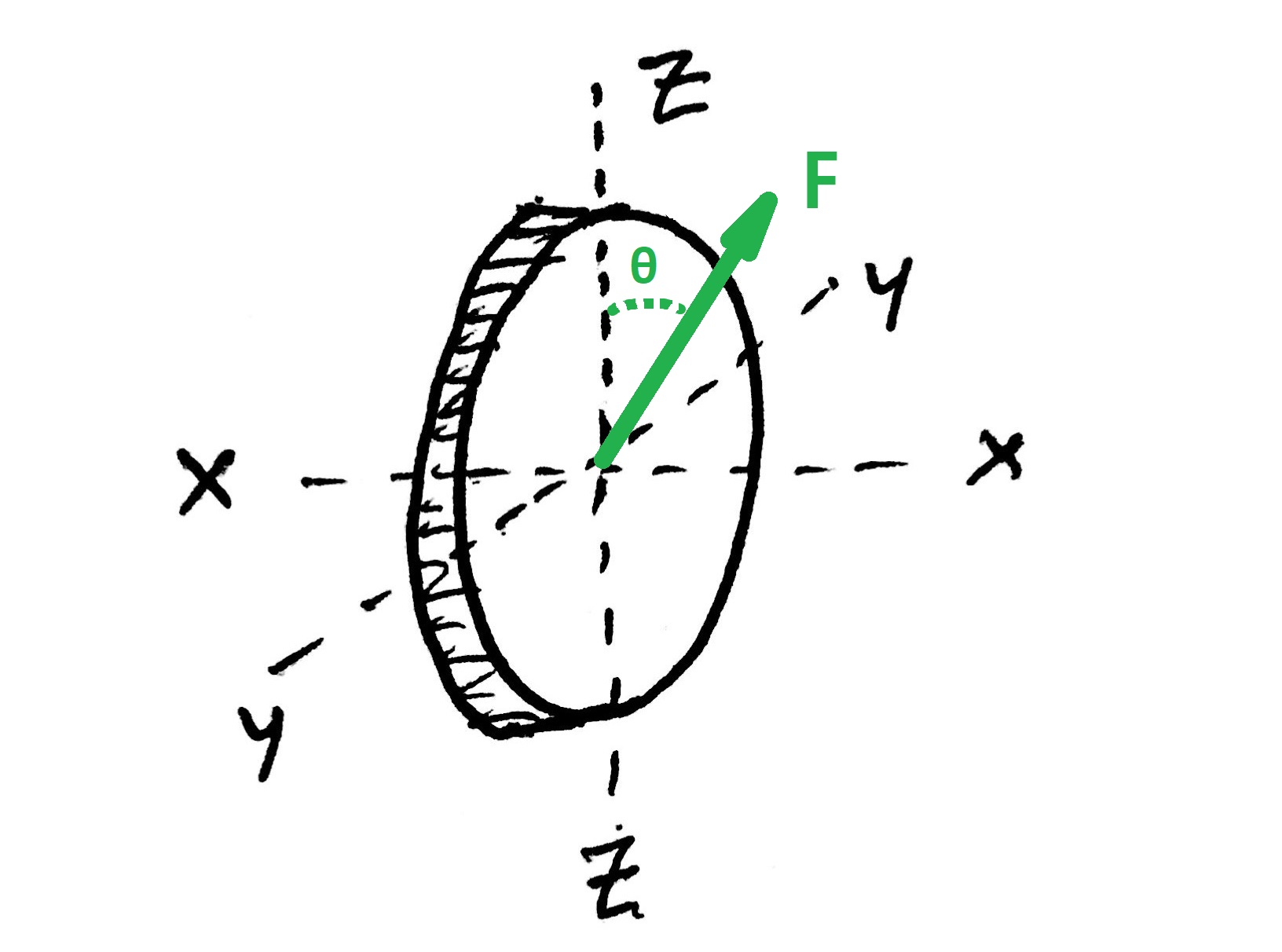
When a force is applied neither tangentially nor normally (as shown in the above fig) then there will be both shear and the normal stress will be induced.

Now we have the idea how the normal stress and the shear stress will be induced by applying the different types of loads.

All we need to do is consider there are so many numbers of planes which are passing thru a single point in an object. All these planes will have the normal stress as well as the shear stress as we mentioned above case iii.

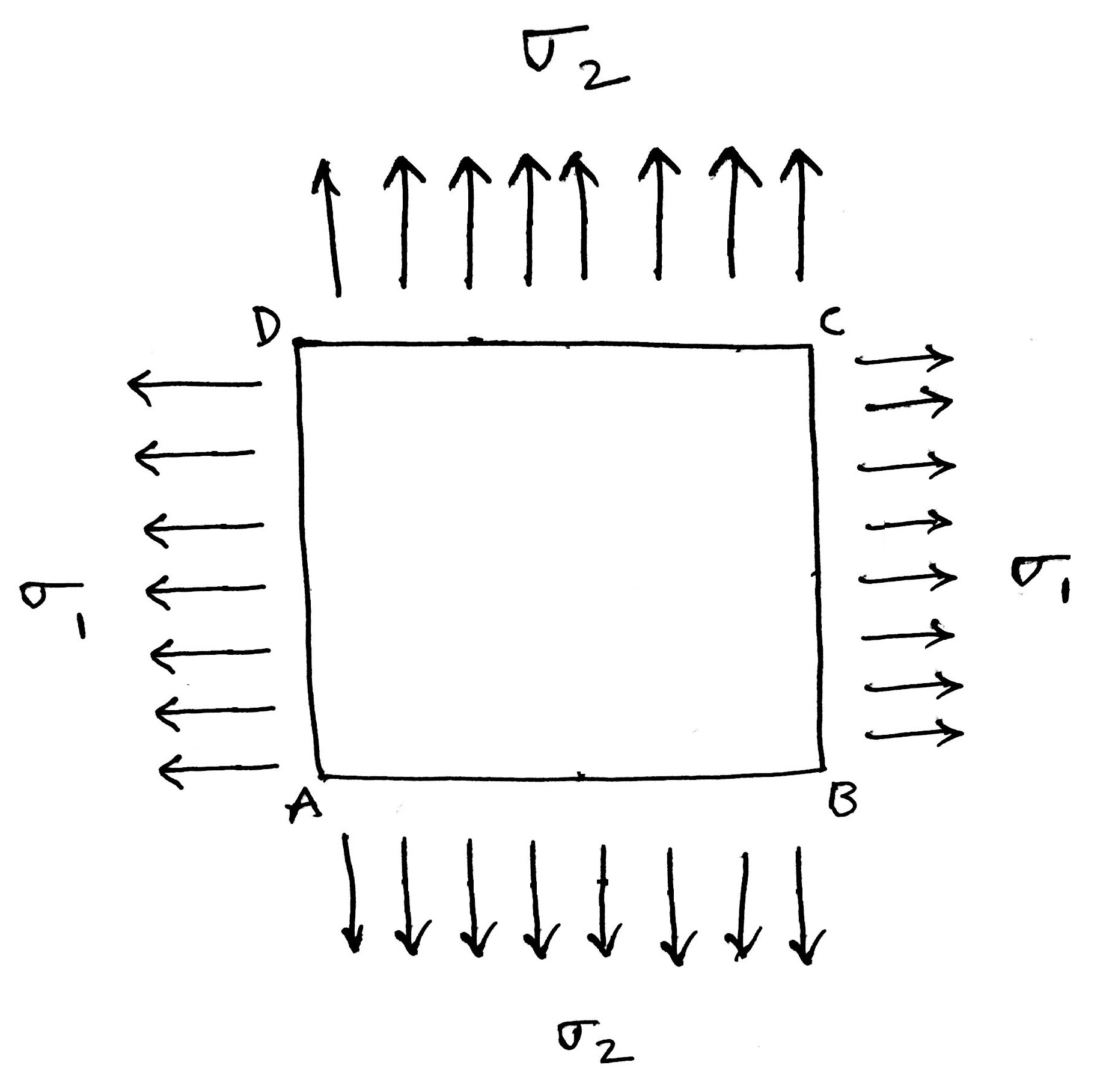
Determination of Principal stresses for a member subjected to the Bi-axial stress

Consider a member ABCD which is subjected to the two mutually perpendicular stresses σ₁ and σ₂ as shown in the below figure.

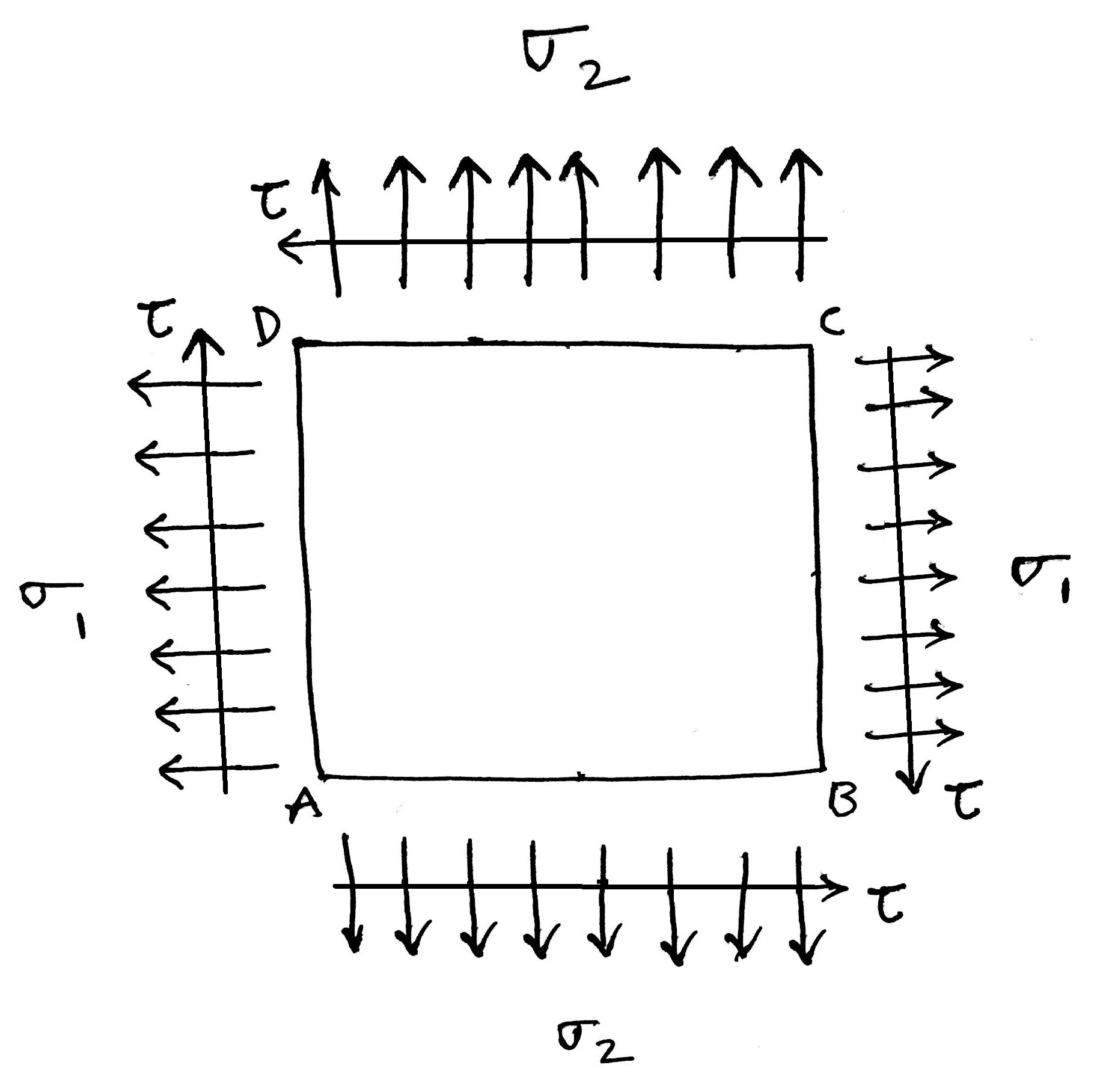
In addition to that normal stress, shear stress will also act as shown in below fig.

The resulted Normal stress and the shear stress will be represented as shown in the below figure.

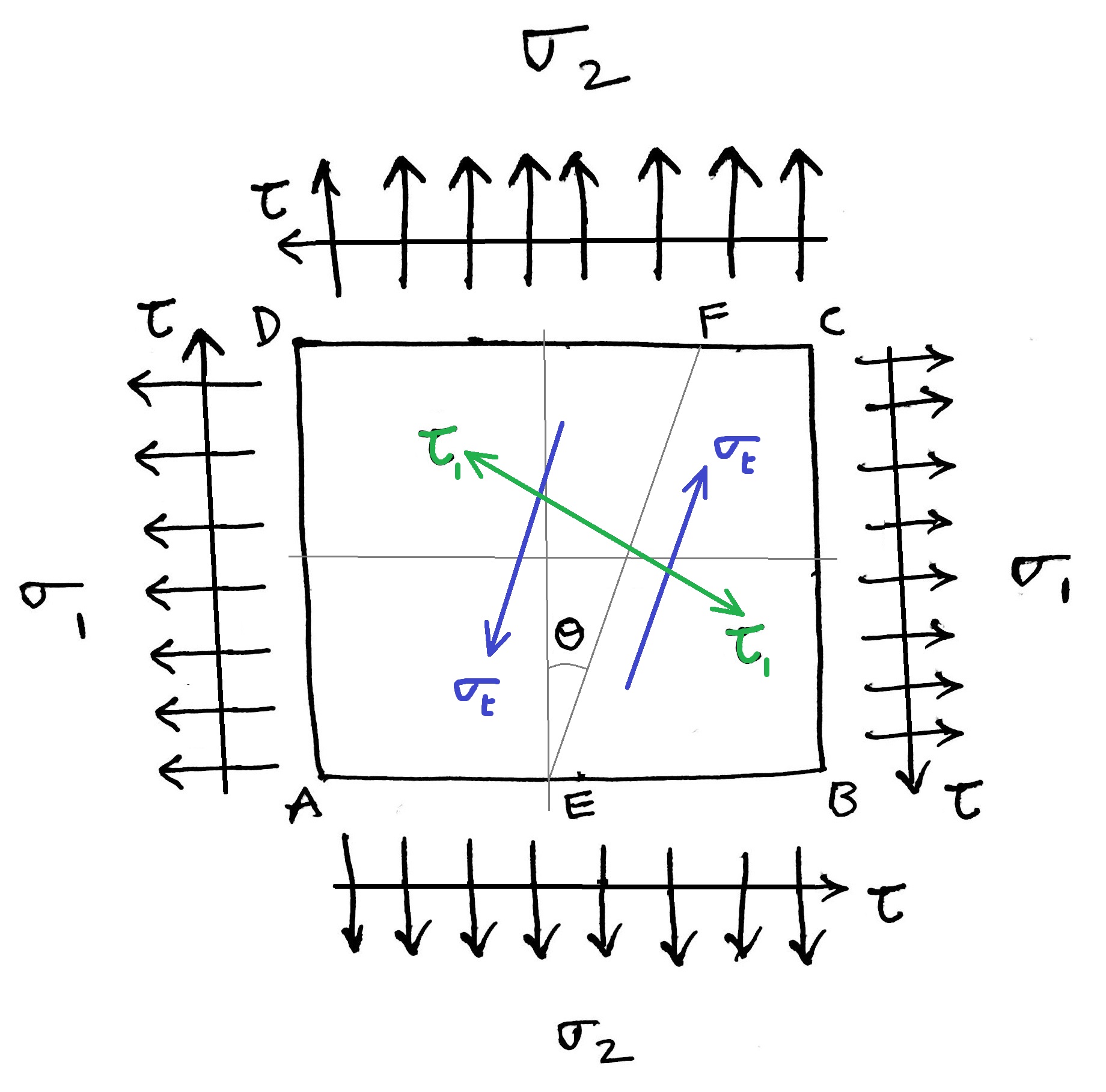
Where EF is an oblique section with an angle θ

We already have some standard formulas to find the Normal stresses and the shear stresses (Referred from the standard textbooks of the strength of materials)

Normal stress is given by

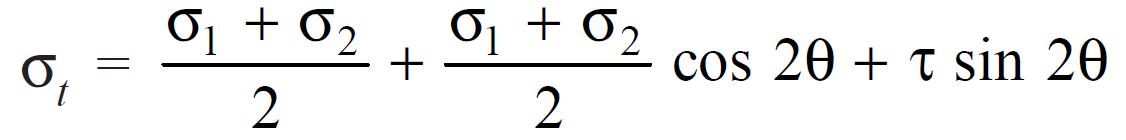
Shear stress is given by (Shear stress will be considered as zero (0) for the finding the principal stresses)

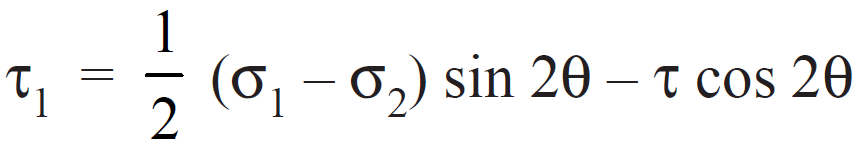
Where

θ = Angle between the principal plane to the normal cross-section.

Here there will be two planes where at one plane will have the maximum stress and the other one will have the minimum stress. the plane at an angle θ where it gives the Maximum stress is known as the Principal stress.