Model Testing of Centrifugal Pumps | Model vs Prototype

The hydraulic machines, which convert the hydraulic energy into mechanical energy, are called turbines while the hydraulic machines which convert mechanical energy into hydraulic energy are called pumps. Hydraulic energy is in the form of pressure energy. If the mechanical energy is converted into pressure energy by means of centrifugal force acting on the fluid, the hydraulic machine is called a centrifugal pump. We discussed How to calculate Work Done, Heads & Efficiencies and Minimum starting speed of Centrifugal Pump. To manufactures these Centrifugal Pumps as a commercial product, We must test them as models/prototypes. In this article let’s do the important calculations involved in the Model Testing of Centrifugal Pumps Prototypes.

Testing of Centrifugal Pumps

Before manufacturing large-sized pumps, We need to build models that are completely similar to the actual pumps (also called prototypes). Tests are conducted on the models and the performance of the prototypes is predicted. The complete similarity between the model and the actual pump (prototype) will exist if the following conditions are satisfied:

Specific speed of the model

Specific speed of model = Specific speed of prototype

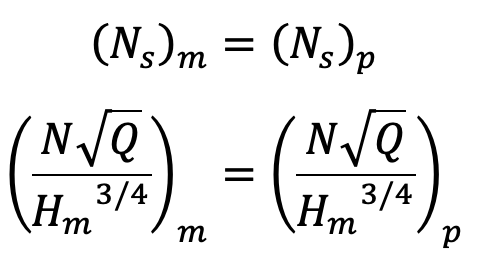
Tangential Velocity

The Tangential Velocity (u) is given by

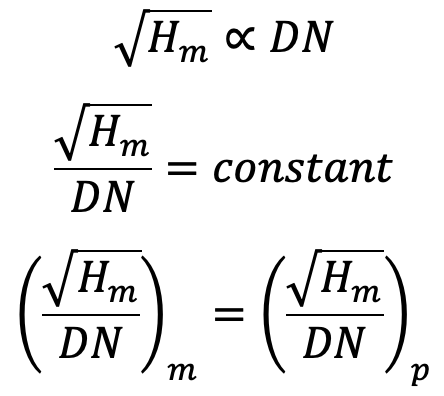
We also know the tangential velocity is given by

Q ∝ D² × V_f
Q ∝ D² × D × N
Q ∝ D³ × N

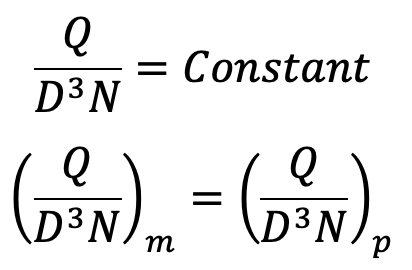
Power of the pump

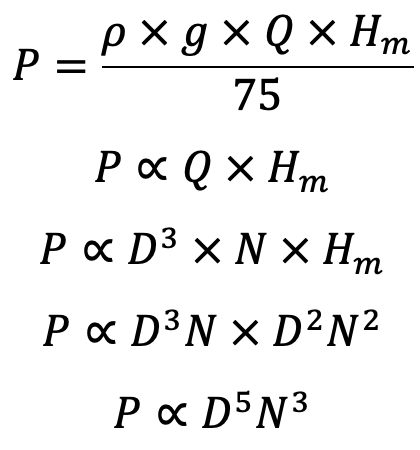
Therefore,

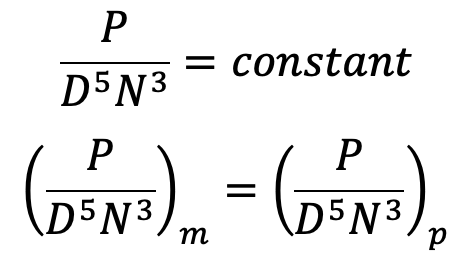
All these parameters should be satisfied in order to design a model. Now let us take an example problem to solve and understand how this theory can be applied to a practical situation.

Calculations for Testing of Centrifugal Pumps

Problem Statement: A one-fifth scale model of a pump was tested in a laboratory at 1000 rpm. The head developed and the power input at the best efficiency point was found to be 8m and 30kW
respectively. If the prototype pump has to work against a head of 25m, determine its working speed, the power required to drive it and the ratio of the flow rates handled by the two pumps.

Answer:

One-fifth scale model means that the ratio of linear dimensions of a model and its prototype is equal to 1/5.

Speed of model N_m = 1000 r.p.m.
Head of the model H_m = 8m
Power of model P_m = 30 kW
Head of the prototype H_p = 25 m

Let
N_p= Speed of prototype
P_p = Power of the prototype
Q_p = Flow rate of prototype
C_m = Flow rate of model

Speed of Prototype

From the above equation (b) we get,

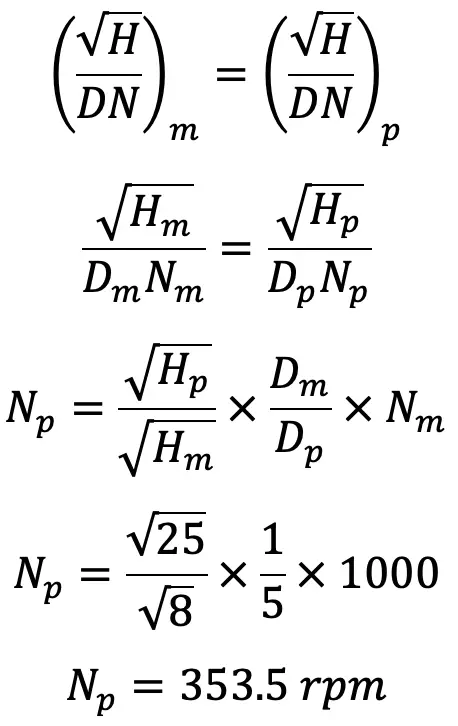
The prototype speed is 353rpm.

Power Developed by Prototype

Using equation (d), we get

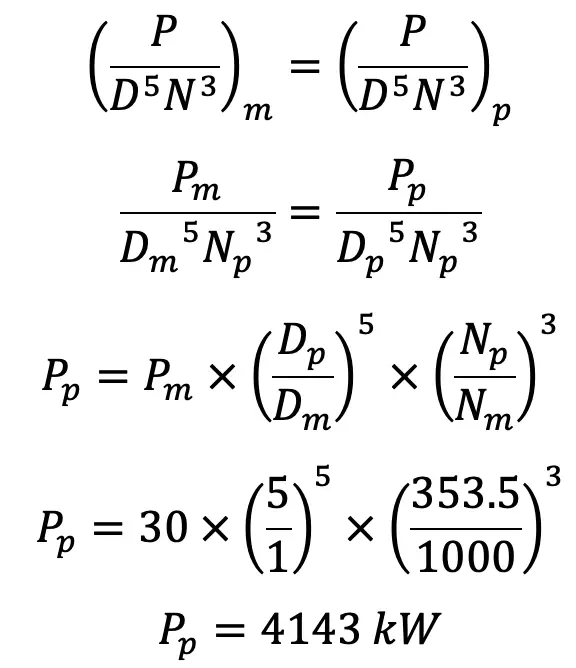
Power Developed by Prototype is 4143 kW.

Ratio of the flow rates of the Model and Prototype

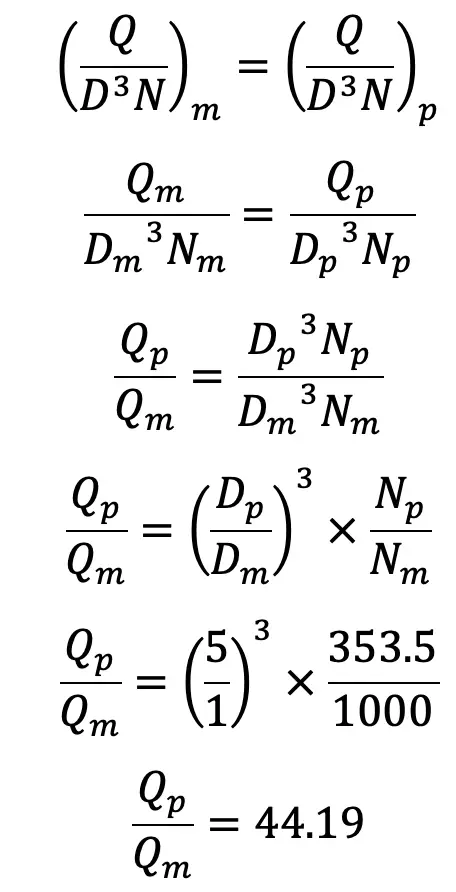
The Ratio of the flow rates of the Model and Prototype is 44.19.

This is how you can calculate the specific speed and the power developed by the model and the prototype with help of this article. Let us know what you think about this in the comment section below.

Do you know what is Priming of a Centrifugal Pump is?
Priming of a centrifugal pump is defined as the operation in which the suction pipe, casing of the pump and a portion of the delivery pipe up to the delivery valve are completely filled up from the outside source with the liquid to be raised by the pump before starting the pump. Thus the air from these parts of the pump is removed and these parts are filled with the liquid to be pumped. The work done by the impeller per unit weight of liquid per sec is known as the heat generated by the pump. Equation (a) from the previous article gives the head generated by the pump as =1/g V_w2 u₂ metre. This equation is independent of the density of the liquid. This means that when the pump is running in the air, the head generated is in terms of metres of air. If the pump is primed with water, the head generated is same metre of water. But as the density of air is very low, the generated head of air in terms of equivalent metre of water head is negligible and hence the water may not be sucked from the pump. To avoid this difficulty, priming is necessary to start the centrifugal pump.