Heads And Efficiencies of a Centrifugal Pump

The hydraulic machines, which convert the hydraulic energy into mechanical energy, are called turbines while the hydraulic machines which convert mechanical energy into hydraulic energy are called pumps. Hydraulic energy is in the form of pressure energy. If the mechanical energy is converted into pressure energy by means of centrifugal force acting on the fluid, the hydraulic machine is called a centrifugal pump. In the previous article, we discussed the details of the Centrifugal Pump such as its construction, its main parts, how the Centrifugal Pump works, the Multistage Centrifugal Pumps and how to calculate the Work Done by The Centrifugal Pump. Let us now discuss the different Heads And Efficiencies of a Centrifugal Pump.

Different Heads of Centrifugal Pump

Following are the different types of heads in Centrifugal Pumps are

1. Suction Head (h_s)
2. Delivery Head (h_d)
3. Static Head (H_s)
4. Manometric Head (H_m)

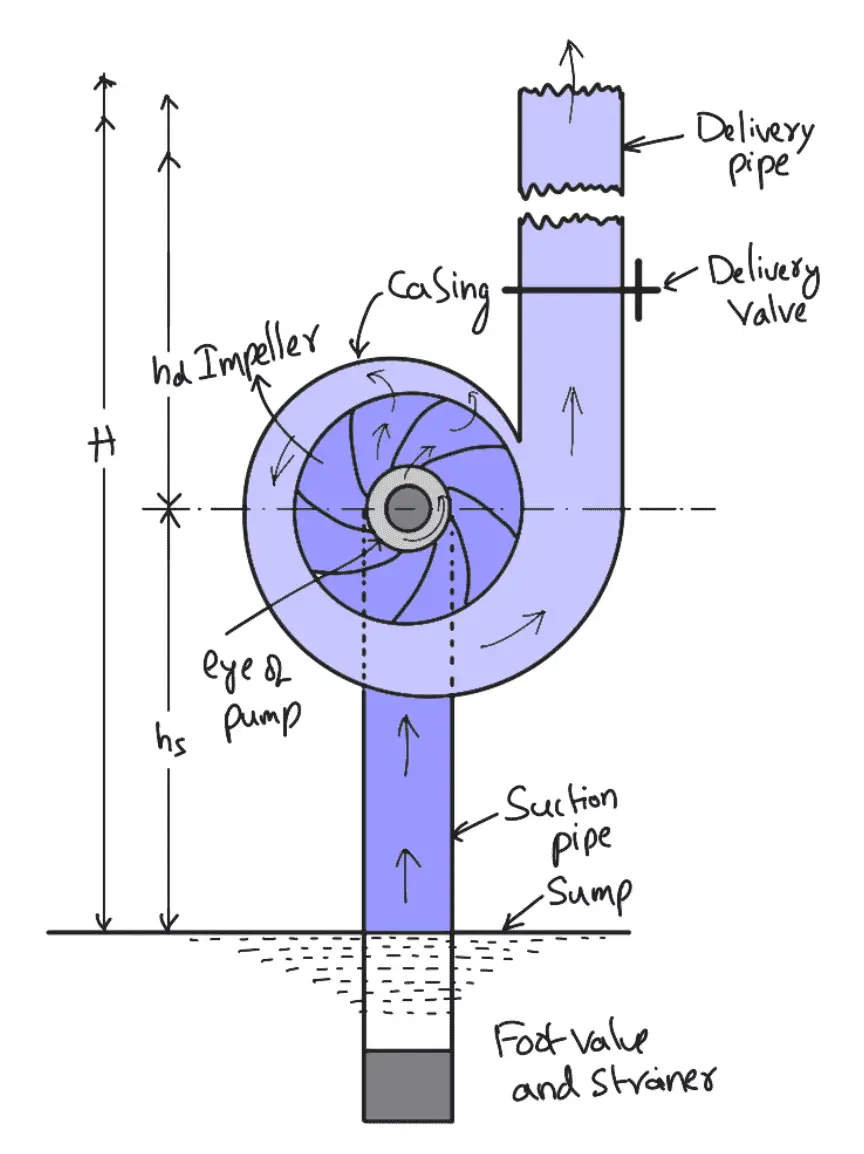
Let us discuss these Heads in detail.

Suction Head (h_s)

It is the vertical height of the centre line of the centrifugal pump above the water surface in the tank or pump from which water is to be lifted as shown in the above figure. This height is also called suction lift and is denoted by ” h_s

Delivery Head (h_d)

The vertical distance between the centre line of the pump and the water surface in the tank to which water is delivered is known as the delivery head. This is denoted by h_d.

Static Head (H_s)

The sum of the suction head and the delivery head is known as the static head. This is represented by ‘ H_s and is written as

H_s = h_s + h_d

Manometric Head (H_m)

The manometric head is defined as the head against which a centrifugal pump has to work. It is denoted by H_m. It is given by the following expressions:

(a)

H_m = Head imparted by the impeller to the water – Loss of head in the pump

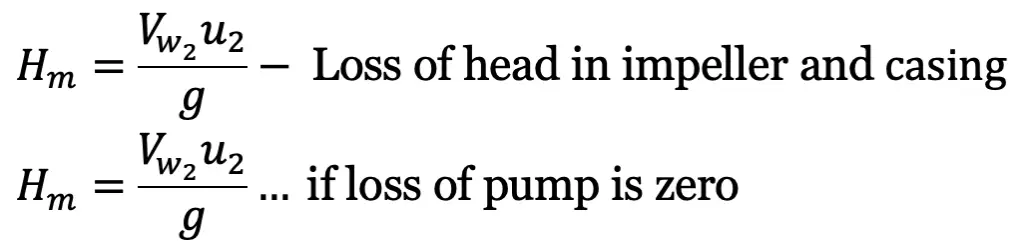
(b)

H_m = Total head at the outlet of the pump – Total head at the inlet of the pump

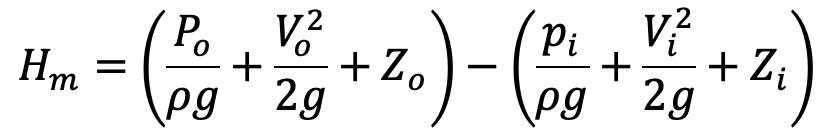
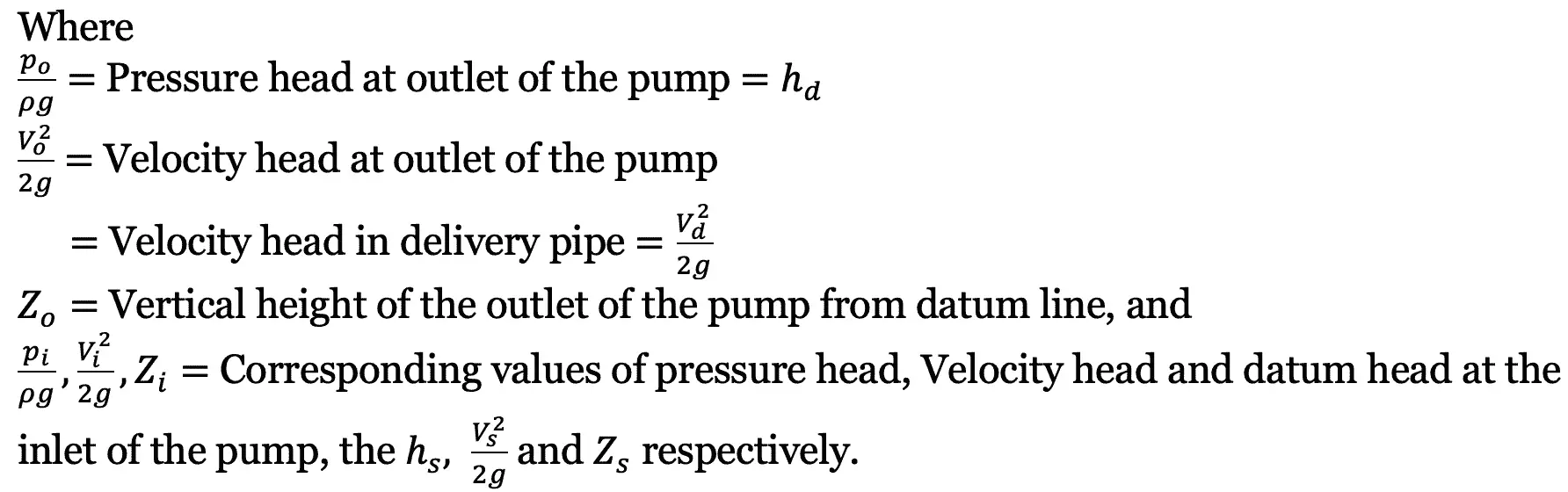
(c)

H_m = h_s + h_d + h_fs + h_fd + V_d²/2g

Where
h_s = Suction head
h_d = Delivery head
h_fs = Frictional Head loss in the suction pipe
h_fd = Frictional head loss in the delivery pipe
V_d = Velocity of water in the delivery pipe

Efficiencies of a Centrifugal Pump

In the case of a centrifugal pump, the power is transmitted from the shaft of the electric motor to the pump’s shaft and then to the impeller. From the impeller, the power is given to the water. Thus power is decreasing from the shaft of the pump to the impeller and then to the water. The following are the important efficiencies of a centrifugal pump:

(a) Manometric efficiency, η_man
(b) Mechanical efficiency, η_m
(c) Overall efficiency, η_o

Manometric efficiency, η_man

The ratio of the manometric head to the head imparted by the impeller to the water is known as manometric efficiency. Mathematically, it is written as

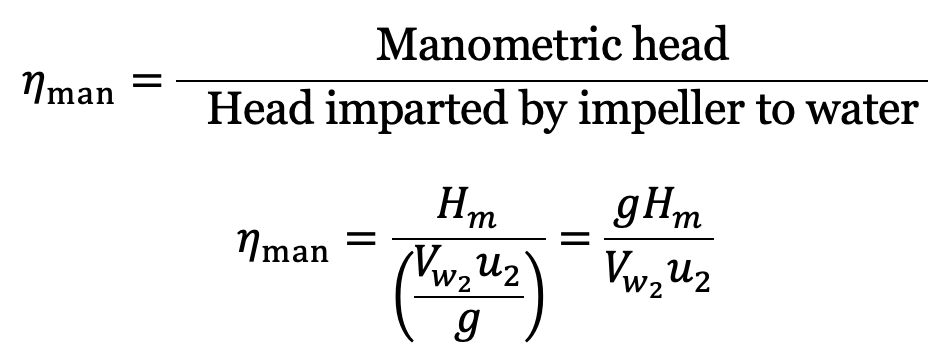
The power at the impeller of the pump is more than the power given to the water at the outlet of the pump. The ratio of the power given to water at the outlet of the pump to the power available at the impeller is known as manometric efficiency.

The power is given to water at the outlet of the pump

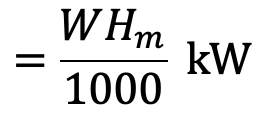
The power at the impeller

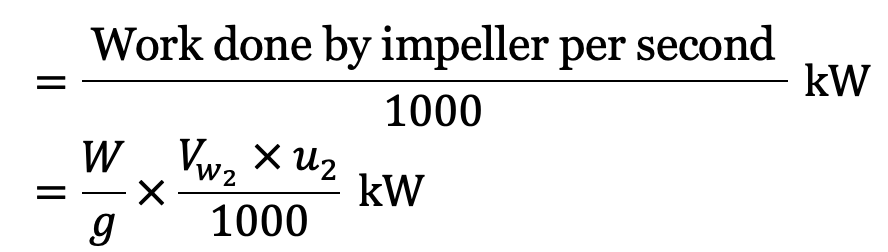
Manometric efficiency

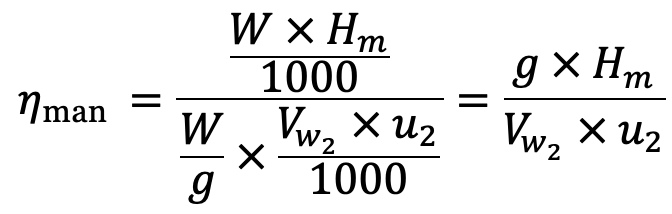
Mechanical efficiency, η_m

The power at the shaft of the centrifugal pump is more than the power available at the impeller of the pump. The ratio of the power available at the impeller to the power at the shaft of the centrifugal pump shaft is known as mechanical efficiency. It is written as

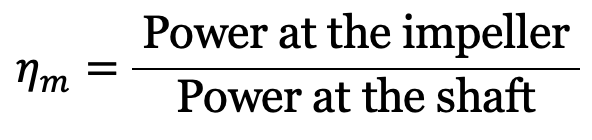
The power at the impeller in kW

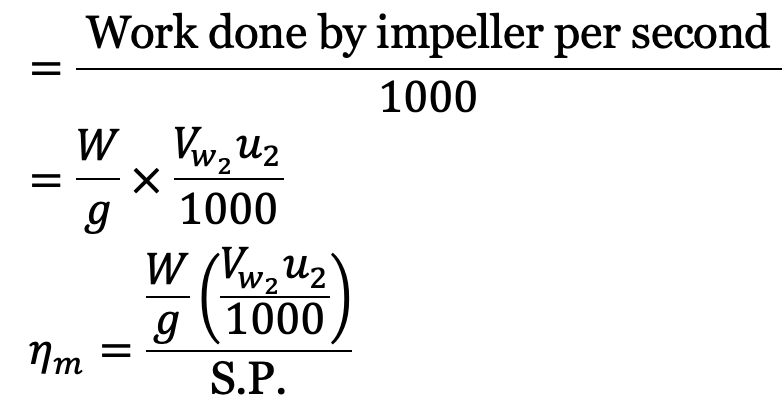
where S.P. = Shaft power.

Overall efficiency, η_o

It is defined as the ratio of the power output of the pump to the power input of the pump. The power output of the pump in kW

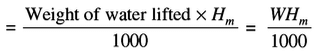
Power input to the pump = Power supplied by the electric motor = S.P. of the pump.

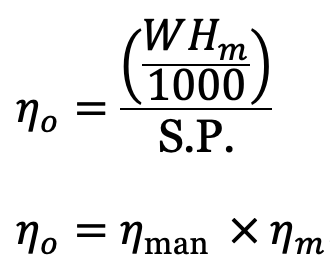
Let us solve an example problem to understand how to calculate the Efficiency of The Centrifugal Pump, the Vane angle of the centrifugal pump and the Loss of Head.

Example Problems on Efficiencies of a Centrifugal Pump

Problem Statement: A centrifugal pump discharges 0.15 m³/s of water against a head of 12.5 m, the speed of the impeller being 600 rpm. The outer and inner diameters of the impeller are 500mm and 250mm respectively and the vanes are bent back at 35° to the tangent at the exit. If the area of flow remains 0.07 m² from the inlet to the outlet, calculate:
(i) Manometric efficiency of the pump
(ii) Vane angle at the inlet
(iii) Loss of head at the inlet to impeller when the discharge is reduced by 40% without changing the speed.

Answer:

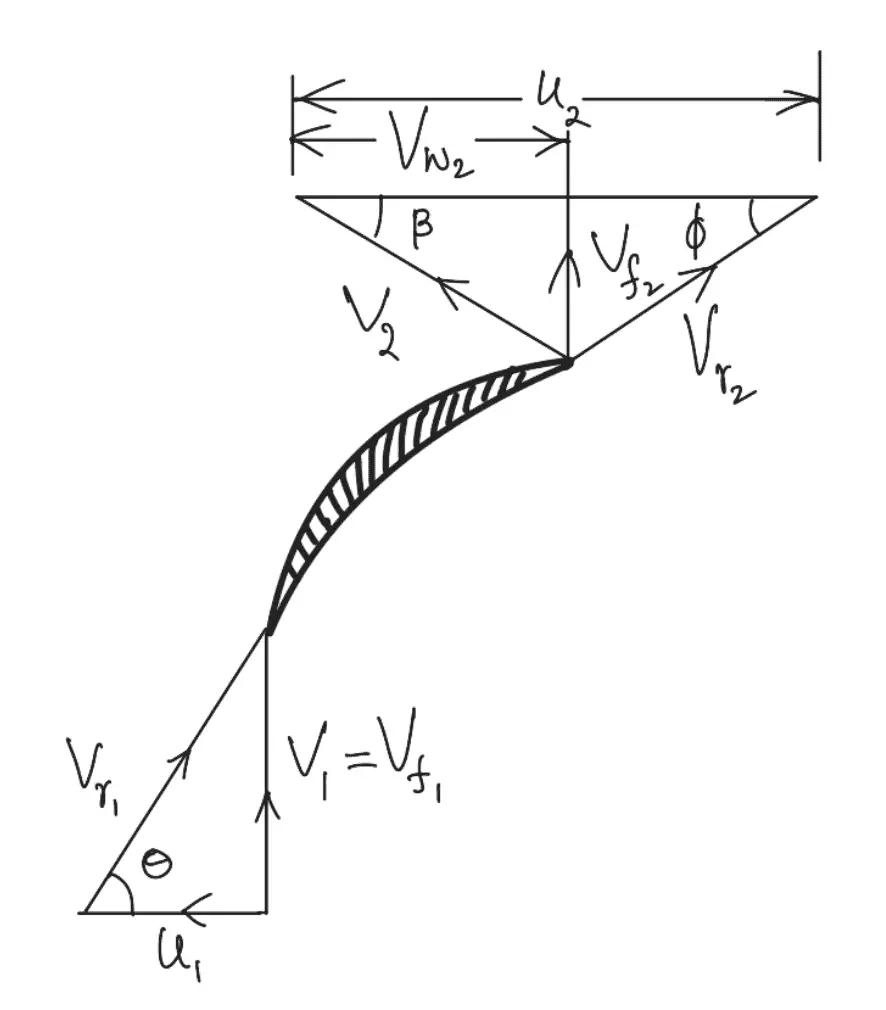
Given data as follows
Discharge Q = 0.15 m³/s
Head H_m = 12.5 m
Speed N = 600 rpm
Outer diameter of the impeller D₂ = 500 mm = 0.5 mm
Inner Diameter of the impeller D₁ = 250mm = 0.25m
Vane angle at the outlet φ = 35°
Area of flow = 0.07 m²

As the area of flow is constant from inlet to outlet, then the velocity of flow will be constant from inlet to outlet.

Discharge = Area of flow × Velocity of flow
0.15 = 0.07 × Velocity of flow
Velocity of flow = 0.15 ÷ 0.07 = 2.14 m/s

V_f1 = V_f2 = 2.14 m/s

The tangential velocity of the impeller at the inlet and outlet are

From outlet velocity triangle

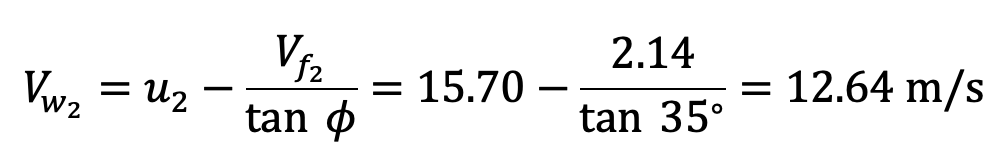
Efficiencies of a Centrifugal Pump

We need to calculate the Manometric Efficiency of the given Centrifugal pump. We have the Manometric efficiency formula from above is

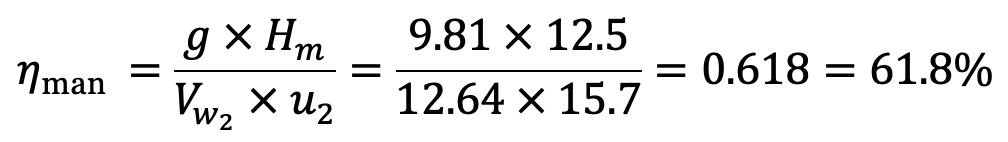
Vane angle at the inlet (θ)

From the inlet velocity triangle,

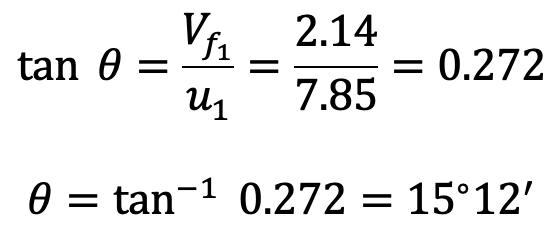
Loss of head

Now let us calculate the Loss of head at the inlet to impeller when discharge is reduced by 40% without changing the speed.

When there is an increase or decrease in the discharge from the normal discharge, a loss of the head occurs at entry due to shock. In this case, discharge is reduced by 40%. Hence the new discharge is given by,

Q* = 0.6 × Q

Where Q = 0.15 m³/s

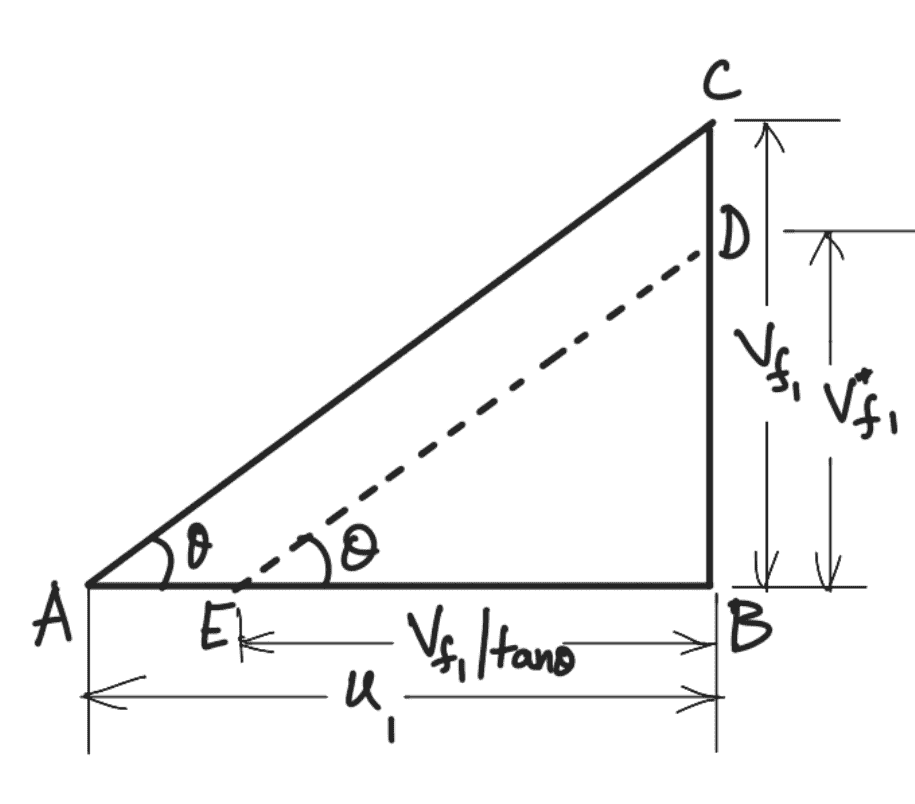
As the area of flow is constant, hence the new velocity of flow(V_f1*) will be given by,

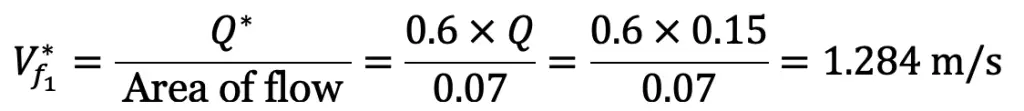
The above figure shows the velocity triangle at the inlet corresponding to normal discharge and reduced discharge. ABC is the velocity triangle due to normal discharge. Triangle BDE is corresponding to reduced discharge BD = 1.284 m/s and DE is parallel to AC.

The blade angle A at the inlet cannot change and hence DE will be parallel to AC. There will be a sudden change in the tangential velocity from AB to BE. Hence due to this shock, there will be a loss of head at the inlet.

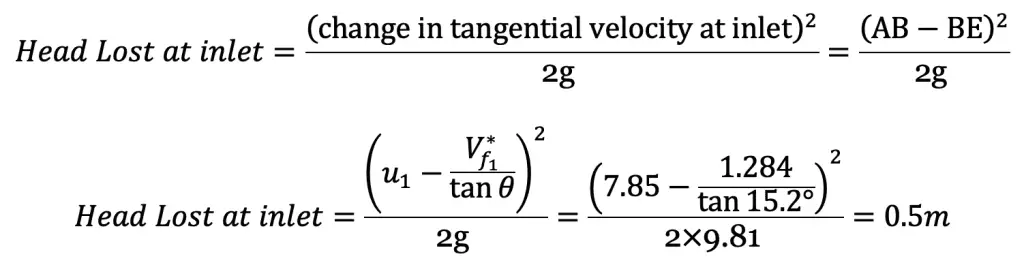
This is how you can calculate the vane angle, Loss of head and Efficiency of the Centrifugal pump. Let us know what you think about this article in the comment section below.