Long Columns Subjected to Eccentric Loading

A machine part subjected to an axial compressive force is called a strut. A strut may be horizontal, inclined, or even vertical. But a vertical strut is a column, pillar, or stanchion. The machine members that must be investigated for column action are piston rods, valve push rods, connecting rods, screw jack, side links of toggle jack, etc. We discussed Euler’s Column Theory for the long columns and Rankine’s Formula for both Short and Long columns for the combined load. At the same time, we discussed Johnson’s Formulae for the short columns made of ductile materials. let us discuss when Long Columns Subjected to Eccentric Loading.

Long Columns Subjected to Eccentric Loading

Long columns have lengths > 30 times their diameter whereas Short columns are the ones that have lengths < 8 times their diameter. We have always referred to the cases when the load acts axially on the column (i.e. the line of action of the load coincides with the axis of the column).

But in actual practice, it is not always possible to have an axial load on the column, and eccentric loading takes place. Here we shall discuss the effect of eccentric loading on Rankine’s and Euler’s formula for long columns.

Consider a long column hinged at both ends and subjected to an eccentric load as shown in the following figure.

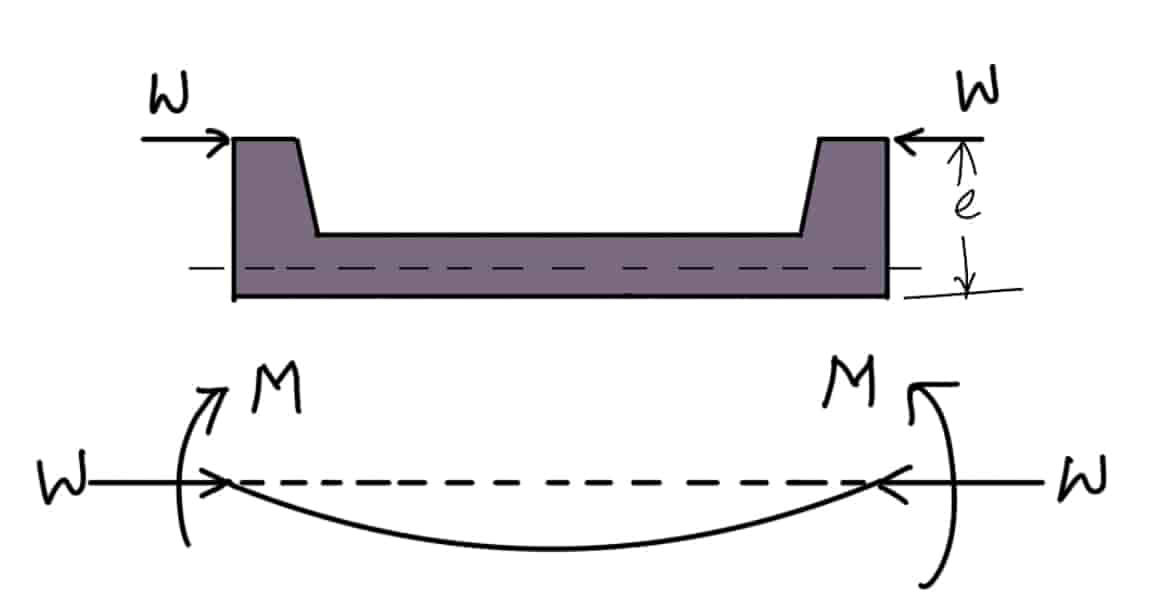
Let
W = Load on the column,
A = Area of cross-section,
e = Eccentricity of the load,
Z = Section modulus,
y_c = Distance of the extreme fiber (on the compression side) from the axis of the column,
k = Least radius of gyration,
I = Moment of inertia = A.k²,
E = Young’s modulus,
l = Length of the column.

We have already discussed that when a column is subjected to an eccentric load, the maximum intensity of compressive stress is given by the relation.

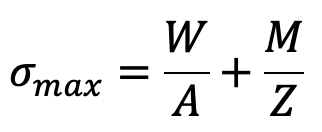
The maximum bending moment for a column hinged at both ends and with eccentric loading is given by

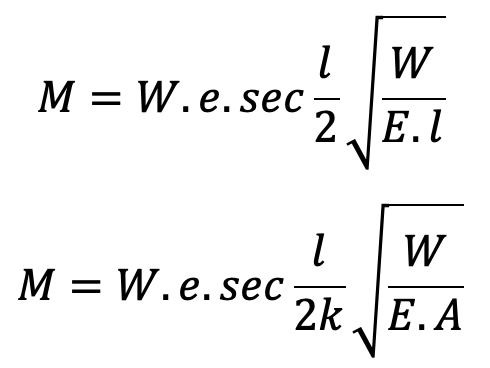
We can substitute the maximum bending moment value in the above maximum compressive stress equation, and we get

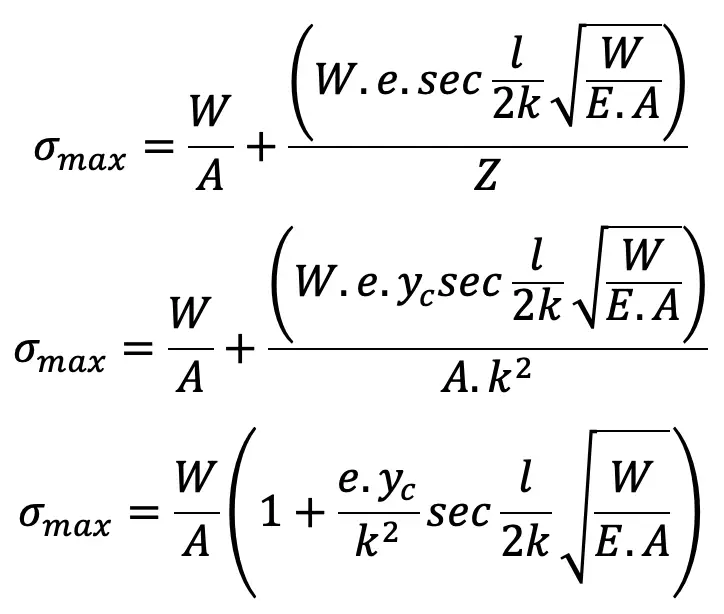
We can also substitute the l = L, since the equivalent length for both ends is hinged.

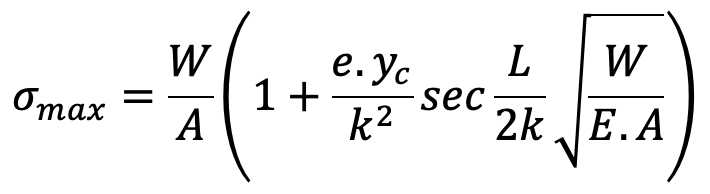
This is the relation we can use to determine the maximum intensity of compressive stress when Long Columns are subjected to Eccentric Loading.

Let us know what you think about this short article about the Long Columns Subjected to Eccentric Loading in the comment section below.