Hydraulic machines are defined as those machines which convert either hydraulic energy (energy possessed by water) into mechanical energy (which is further converted into electrical energy ) or mechanical energy into hydraulic energy. The hydraulic machines, which convert the hydraulic energy into mechanical energy, are called turbines while the hydraulic machines which convert the mechanical energy into hydraulic energy are called pumps. We discussed different types of Hydraulic turbines in the previous article. Turbine Specific Speed is the speed of a turbine which is identical in shape, geometrical dimensions, blade angles, gate opening etc., with the actual turbine but of such a size that it will develop unit power when working under the unit head. Let us discuss more on Specific Speed and the Specific Speed derivation.

Turbine Specific Speed
As we have already mentioned the Specific Speed is the speed of a turbine which is identical in shape, geometrical dimensions, blade angles, gate opening etc., with the actual turbine but of such a size that it will develop unit power when working under the unit head. It is denoted by the symbol N. The specific speed is used in comparing the different types of turbines as every type of turbine has a different specific speed.
In M.K.S. units, unit power is taken as one horsepower and unit head as one meter.
In S.I. units, unit power is taken as one kilowatt and unit head as one meter.
Turbine Specific Speed Derivation
The overall efficiency (ηo) of any turbine is given by,
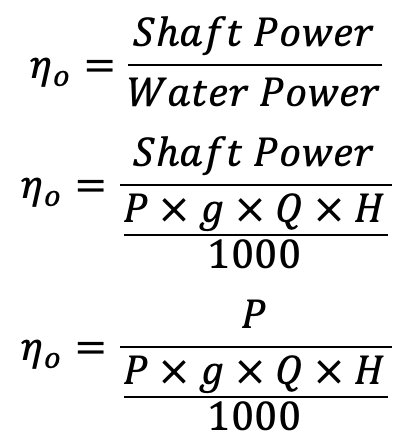
where
H = Head under which the turbine is working
Q = Discharge through the turbine
P = Power developed or shaft power
From the above equation (a)
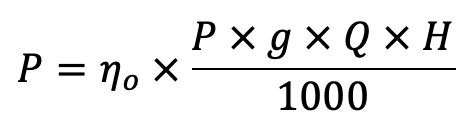
P ∝ Q × H (as ηo and ρ are constant)
….. Equation (b)
Now let
D = Diameter of the actual turbine,
N = Speed of actual turbine,
u = Tangential velocity of the turbine,
Ns = Specific speed of the turbine
V = Absolute velocity of the water
The absolute velocity, tangential velocity and head on the turbine are related as
u ∝ V where V ∝ √H
u ∝ √H
But the tangential velocity u is given by
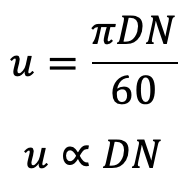
From the above two equations, we have
√H ∝ DN
D ∝ √H / N
The discharge through the turbine is given by Q = Area × Velocity
Area ∝ B × D
Area ∝ D2
Velocity ∝ √H
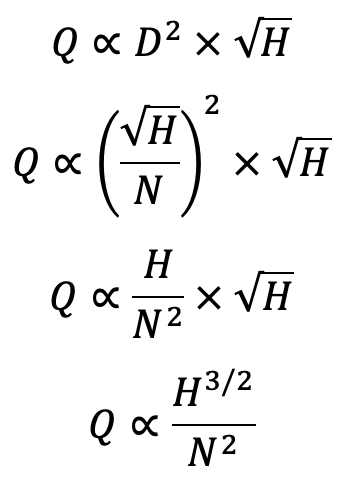
Substituting the value of Q in equation (b),
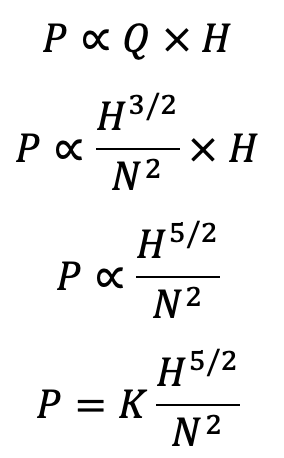
where K = Constant of proportionality
if P = 1, H= 1, the speed N = Specific speed Ns.
Substituting these values in the above equation, we get
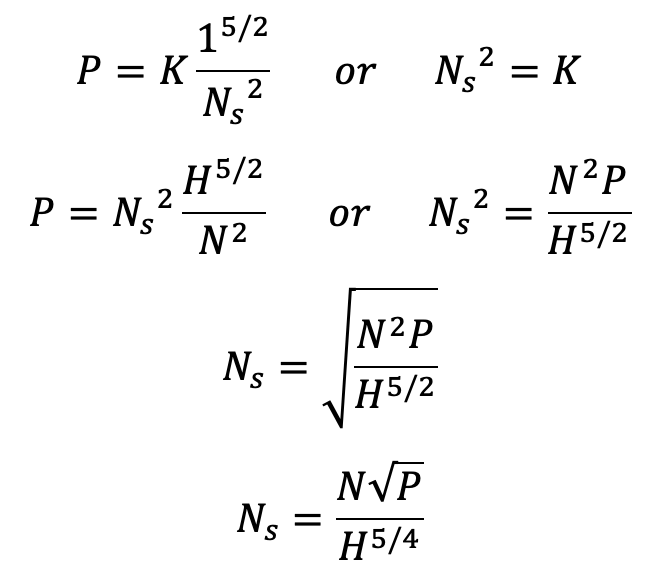
In equation (c), if P is taken in metric horsepower the specific speed is obtained in M.K.S. units.
But if P is taken in kilowatts, the specific speed is obtained in S.I. units.
Significance of Specific Speed
Specific speed plays an important role in selecting the type of turbine. Also, the performance of a turbine can be predicted by knowing the specific speed of the turbine. The type of turbine for different specific speeds is given in the following Table:
| S.No | Specific Speed (M.K.S) | Specific Speed (S.I) | Types of Turbine |
| 1 | 10 to 35 | 8.5 to 30 | Pelton wheel with a single jet |
| 2 | 35 to 60 | 30 to 51 | Pelton wheel with two or more jets |
| 3 | 60 to 300 | 51 to 225 | Francis Turbine |
| 4 | 300 to 1000 | 225 to 860 | Kaplan or Propeller turbine |
Example Problem To Calculate Specific Speed
Problem Statement: A turbine develops 7225 kW power under a head of 25 metres at 135rpm. Calculate the specific speed of the turbine and state the type of the turbine.
Answer:
Solution. Given :
Power developed,
P = 7225 kW Head,
H = 25 m Speed,
N= 135 r.p.m. Specific speed of the turbine (Ns)
Using equation (c),
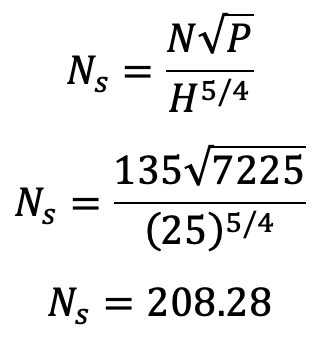
From the above Table, for specific speeds (S.I.) between 51 and 255, the type of turbine is Francis Turbine. The specific speed of 205.28 lies in this range and the type of turbine is Francis.
Would you like to solve an example by yourself?
A turbine is to operate under a head of 25m at 200 r.p.m. The discharge is 9 cumec (m3/s). If the efficiency is 90%:
1. Calculate the Power of the Turbine
2. Calculate the Specific speed of the Turbine
3. Determine the Type of turbine
Would you like to solve it and let us know the answer in the comment section below?

Leave a Reply