How to calculate the Coefficient of Friction?

Do you know what is Friction? When a body moves or tends to move over another body, a force opposing the motion develops at the contact surfaces. The force which opposes the movement or the tendency of movement is called the frictional force or simply friction. We feel the contacting surfaces to be smooth. Actually, in almost all cases the contacting surfaces are not smooth. There are minutely projecting particles that are invisible to the naked eye that develops frictional force to oppose the tendency to a movement of one surface over the other surface. In this article, the additional terminology Coefficient of Friction used in connection with frictional forces is explained and laws of friction (dry) are discussed.

We have discussed how to find resultant forces in truss elements and beams, please refer to them before proceeding with the Calculation of the Coefficient of friction. If you have a little bit of idea about them then go ahead and proceed.

Coefficient of Friction

Whenever a resultant force acts in the direction of contacting surfaces frictional force develops to oppose that force. The frictional force, like any other reaction, has a remarkable property of adjusting itself in magnitude to the tangential force.

However, there is a limit beyond which the magnitude of the frictional force will not develop. If the applied tangential force is more than this maximum frictional force, there will be movement of one body over the other body with acceleration as per Newton’s second law of mass times acceleration equal to the resultant force. Also stated as Law of Acceleration.

F = ma

This maximum value of frictional force, which comes into play when the motion is impending is known as Limiting Friction.

• It may be noted that when the applied tangential force is less than the limiting friction, the body remains at rest and such friction is called Static Friction, which will have any value between zero and limiting friction.
• If the value of applied tangential force exceeds the limiting friction, the body starts moving over another body and the frictional resistance experienced while moving is known as Dynamic Friction.

The magnitude of dynamic friction is found to be less than limiting friction. Dynamic friction may be further classified into two groups:

(i) Sliding Friction: It is the friction experienced by a body when it slides over the other body.
(ii) Rolling Friction: It is the friction experienced by a body when it rolls over another body.

It has been experimentally proved that, between two contacting surfaces, the magnitude of limiting friction bears a constant ratio to the normal reaction between the two and this ratio is called Coefficient of Friction.

Let us consider a body weighing W is being pulled by a force P and the motion is impending.

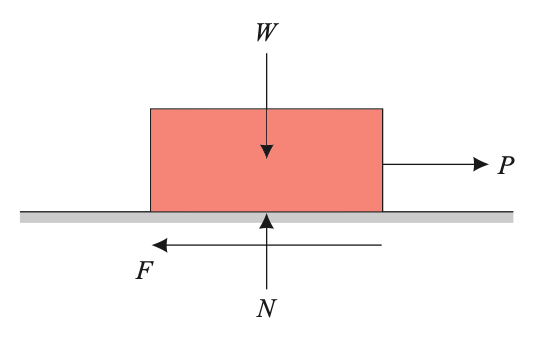
Let N be the normal reaction and F the limiting frictional force.

Then Coefficient of Friction = F/N

The coefficient of friction is denoted by µ. Then

µ = F/N

This is the formula for the Coefficient of Friction. Before we calculate the coefficient of friction for any object sliding, it is required to understand some of the laws of friction.

Laws of Friction

The following principles are the experimental studies by Coulomb (1781) and by Mosin (1831). These principles constitute the laws of dry friction and may be called Coulomb’s laws of dry friction.

1. The frictional force always acts in a direction opposite to that in which the body tends to move.
2. Till the limiting value is reached, the magnitude of frictional force is exactly equal to the tangential force which tends to move the body.
3. The magnitude of the limiting friction bears a constant ratio to the normal reaction between the two contacting surfaces.
4. The force of friction depends upon the roughness/smoothness of the surfaces.
5. The force of friction is independent of the area of contact between the two surfaces.
6. After the body starts moving, the dynamic friction comes into play, the magnitude of which is less than that of limiting friction and it bears a constant ratio to the normal force. This ratio is called the coefficient of dynamic friction

Following are the some of important parameters while dealing with the Coefficient of Friction. Those are

• Angle of Friction
• Angle of Repose
• Cone of Friction

Angle of Friction

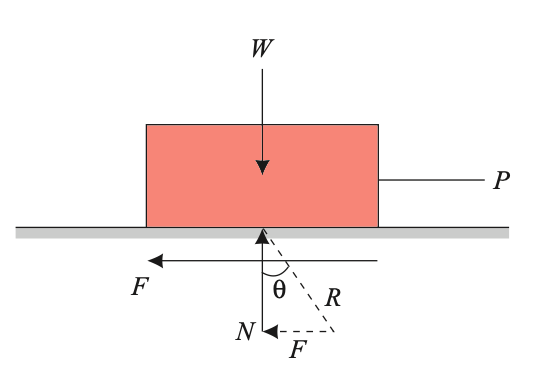
Consider the block as shown in the above figure subject to pull P.

Let F be the frictional force developed and N the normal reaction.

Thus, at the contact surface, the reactions are F and N.

They can be combined to get the resultant reaction R which acts at angle θ to normal reaction.

This angle is given by
tan θ = F/N

As the frictional force increases the angle θ increases and it can reach the maximum value α when the limiting value of friction is reached. Thus, when motion is impending

tan α = F/N = µ

and this value of α is called the angle of limiting friction.

Hence, the angle of limiting friction can be defined as the angle between the resultant reaction and the normal plane on which the motion of the body is impending.

Angle of Repose

It is very well-known that when grains (food grains, sand, cement, soil, etc.) are heaped, there exists a
limit for the inclination of the heap. Beyond that, the grains start rolling down. The limiting angle up to
which the grains repose (sleep) is called the angle of repose.

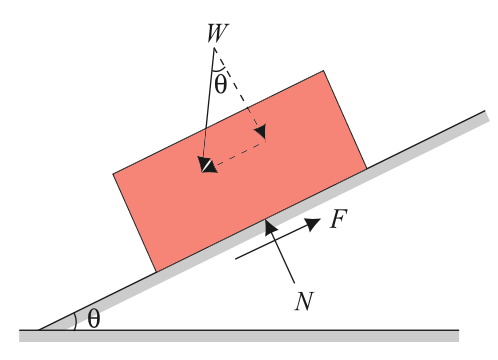
Now consider the block of weight W shown in the above figure which is resting on an inclined plane that makes angle θ with the horizontal.

When θ is a small, block rests on the plane.

If θ is increased gradually a stage is reached at which the block starts sliding.

The angle made by the plane with the horizontal is called the angle of friction for the contacting surfaces.

Thus, the maximum inclination of the plane on which the body, free from external forces, can repose is called the Angle of Repose.

Consider the equilibrium of the block shown in the above figure Since the surface of contact is not smooth,
not only a normal reaction but frictional force also develops. As the body tends to slide down, the
frictional resistance will be up the plane.

Σ Forces normal to plane = 0, gives

N = W cos θ

Σ Forces parallel to plane = 0, gives

F = W sin θ

Dividing above two equations, we get,

F/N = tan θ

If φ is the value of θ when motion is impending, frictional force will be limiting friction and hence

tan φ = F/N

tan φ = µ = tan α
φ = α.

Thus, the value of the angle of repose is the same as the value of the limiting angle of friction.

Cone of Friction

When a body is having impending motion in the direction of P, the frictional force will be the limiting friction and the resultant reaction R will make limiting frictional angle α with the normal as shown in the below figure.

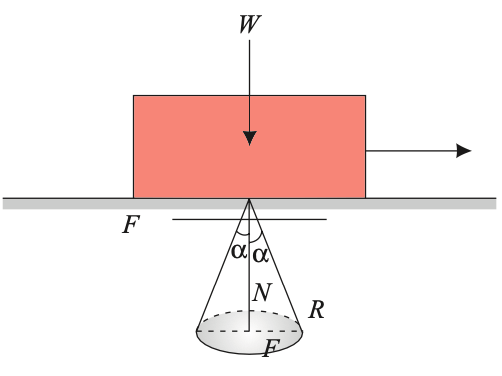
If the body is having impending motion in some other direction, the resultant reaction makes limiting frictional angle α with the normal.

Thus, if the direction of force P is gradually changed through 360°, the resultant R generates a right circular cone with semi central angle equal to α.

If the resultant reaction lies on the surface of this inverted right circular cone whose semi-central angle is limiting frictional angle α, the motion of the body is impending. If the resultant is within this cone the body is stationary.

This inverted cone with semi central angle, equal to the limiting frictional angle α, is called the Cone of Friction.

Example Problems to calculate Coefficient of Friction of Blocks Resting On Horizontal And Inclined Planes

Problem statement 1: A block weighing 500 N just starts moving down a rough inclined plane when it is subjected to 200 N force acting up the inclined plane and it is at the point of moving up the plane when pulled up by a force of 300 N parallel to the plane. Find the inclination of the plane and the coefficient of friction between the inclined plane and the block.

Solution:

The free-body diagram of the block when its motion is impending down the plane is shown in Figure (a) and when it is moving up the plane is shown in Figure (b).

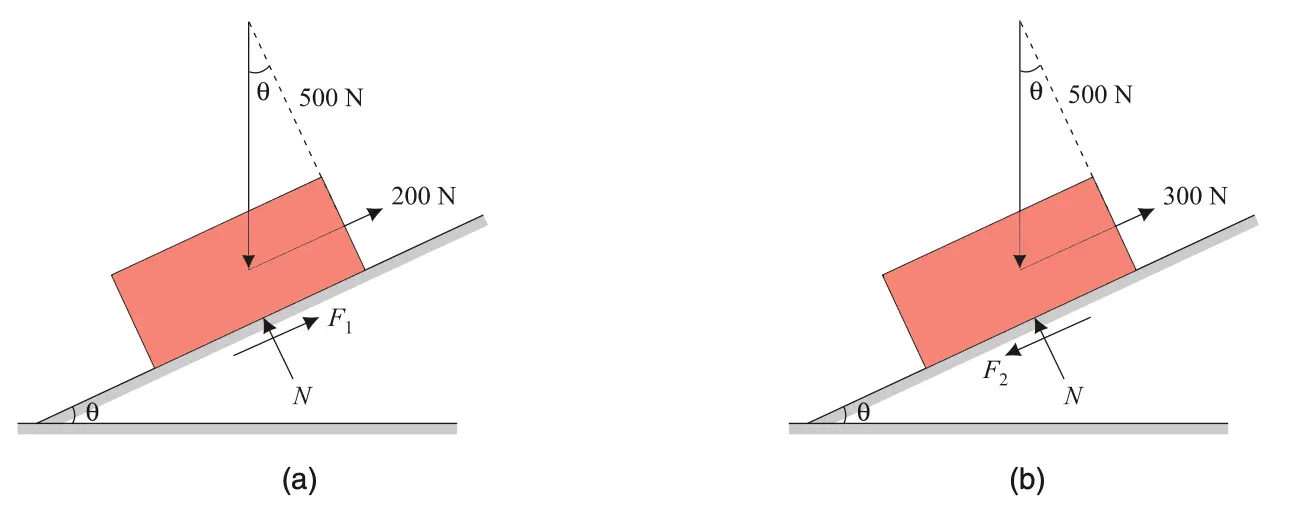
When the block starts moving down the plane [figure (a)]

Frictional forces oppose the direction of the movement.

Hence F₁ is up the plane and F₂ down the plane. Since it is a limiting case

F/N = µ

Σ forces perpendicular to the plane = 0 →

N – 500 cos θ = 0 or N = 500 cos θ …(i)

From law of friction,

F₁ = µN = 500 µ cos θ …(ii)

Σ Forces parallel to the plane = 0 →

F₁ + 200 – 500 sin θ = 0 …(iii)

Substituting the value of F₁ from Equation (ii), we get

500 sin θ – 500 µ cos θ = 200 …(iii)

When the block starts moving up the plane [Figure (b)]

Σ Forces perpendicular to the plane = 0 →

N – 500 cos θ = 0 i.e., N = 500 cos θ …(iv)

From law of friction,

F₂ = µN = 500 µ cos θ …(v)

Σ Forces parallel to the plane = 0 →

300 – 500 sin θ – F₂ = 0
500 sin θ + 500 µ cos θ = 300 …(vi)

Adding equations (iii) and (vi), we get

1000 sin θ = 500
sin θ = 0.5
Hence θ = 30°

The inclination of the plane is 30°

Let us Substitute it in equation (vi), we get the coefficient of friction.

500 sin 30 + 500 µ cos 30 = 300
500 µ cos 30 = 300 – 250 = 50
µ = 50/500 cos 30
∴µ = 0.115

The coefficient of friction (µ) between the inclined plane and the block is 0.115.

Let us solve another example on the Block Resting On Horizontal And Inclined Planes

Problem statement 2: Block A weighing 1000 N rests over block B which weighs 2000 N as shown below Figure. Block A is tied to a wall with a horizontal string. Consider the coefficient of friction between A and B is 1/4 and that between B and the floor is 1/3. Calculate the force P required to create impending motion if
(a) P is horizontal
(b) P acts 30° upwards to horizontal

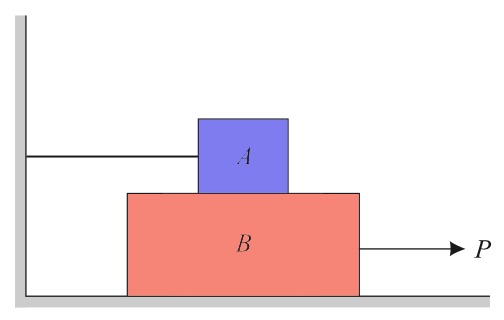
Solution:

(a) When P is horizontal

The free-body diagrams of the two blocks are shown below Figure.

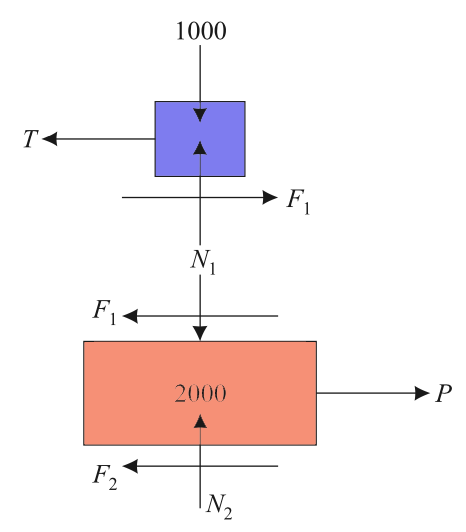
Note the frictional forces are to be marked in the opposite directions of impending relative motion.

In this problem, block B is having an impending move to the right. Hence on it F₁ and F₂ are towards the right.

The relative motion of block A with respect to B is to the left. Hence the direction of F₁ in this is towards the right.

Another way of thinking for the direction of F₁ in the case of block A can be actions and “reactions are equal and opposite”.

Hence on block B if F₁ is towards the left, on A it should be towards the right.

Now consider the equilibrium of block A.

∑ F_V = 0 →
N₁ – 1000 = 0
N₁ = 1000 newton.

Since F₁ is limiting friction,

F₁/N₁ = µ₁ = 1/4
F₁ = 1/4 X1000
∴ F₁ = 250 newton.

∑ F_H = 0 →
F₁ – T = 0 or T = F₁,
T = 250 newton.

Consider the equilibrium of block B.

∑ F_V = 0 →
N₂ – N₁ – 2000 = 0.
N₂ = N₁ + 2000
N₂ = 1000 + 2000
∴ N₂ = 3000 newton.

Since F₂ is limiting friction,

F₂ = µ₂ N₂
F₂ = 1/3X3000
F₂ = 1000 newton.

∑ F_H = 0 →
P – F₁ – F₂ = 0
P = F₁ + F₂ = 250 + 1000
∴ P = 1250 newton

The force P required to create impending motion if it acts horizontally is 1250 newton.

(b) When P is inclined

Free body diagrams for this case are shown in the below figure.

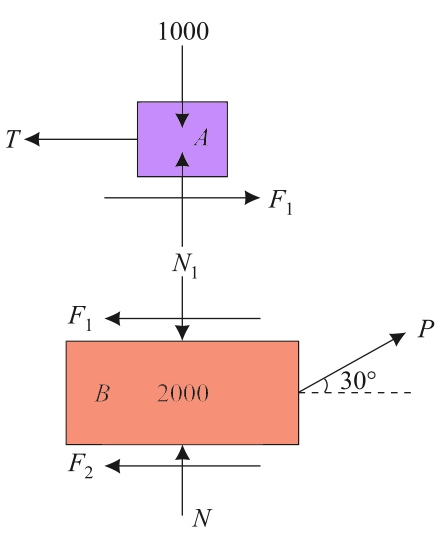
Considering equilibrium of block A, we get

∑ F_V = 0 →
N₁ = 1000 newton.
F1 = 1/4X1000
∴ F1 = 250 newton.
∑ F_H = 0 →
T = F₁ = 250 newton.

Consider the equilibrium of block B.

∑ F_V = 0 →
N₂ – 2000 – N₁ + P sin 30 = 0
N₂ – 2000 – 1000 + P sin 30 = 0
N₂ + 0.5P = 3000

From law of friction

F₂ = µ₂N₂
F₂ = 1/3X(3000 – 0.5P)
F₂ = 1000 – 0.5/3P

∑F_H = 0 →
P cos30 – F₁ – F₂ = 0
P cos 30 – 250 –[1000- (0.5 /3P)] =0
P[ cos 30+0.5/3p] = 1250
P = 1210.4 newton

The force P required to create impending motion if it acts inclined is 1250 newton.

Let us solve one more example on the Block Resting On Inclined Planes to make a motion.

Problem Statement 3: What should be the value of θ as shown in the below figure which will make the motion of 900 N block down the plane to impend? Consider the coefficient of friction for all contact surfaces is 1/3.

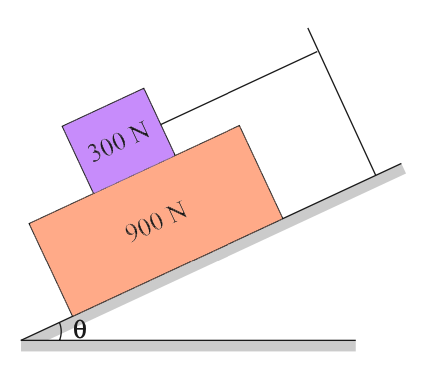
Solution:

900 N block is on the verge of moving downward. Hence frictional forces F₁ and F₂ as shown in the figure act up the plane on 900 N block. Free body diagrams of the blocks are as shown in the below figure.

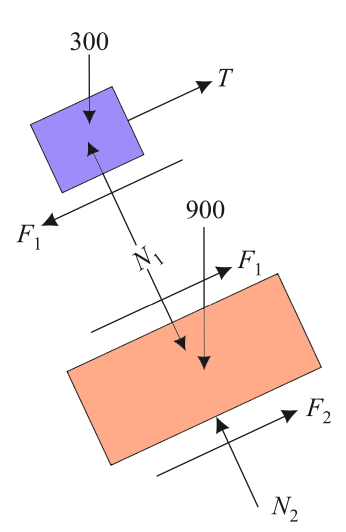
Consider the equilibrium of the 300 N block.

Σ Forces normal to plane = 0 →

N₁ – 300 cos θ = 0
N₁ = 300 cos θ

From law of friction,

F₁ = 1/3N₁
F₁ = 100 cos θ

For 900 N block:

Σ Forces normal to plane = 0 →

N₂ – N₁ – 900 cos θ = 0
N₂ = N₁ + 900 cos θ
N₂ = 300 cos θ + 900 cos θ
N₂ = 1200 cos θ.

From law of friction,

F₂ = µ₂N₂
F₂ = 1/3 X 1200 cos θ
F₂ = 400 cos θ

Σ Forces parallel to the plane = 0 →

F₁ + F₂ – 900 sin θ = 0
100 cos θ + 400 cos θ = 900 sin θ
∴ tan θ = 500/900
∴ θ = 29.05°

With a θ value of 29.05° will make the motion of 900 N block down the plane to impend.

Conclusion

We have discussed the laws of friction and discussed how we can calculate the coefficient of friction with 3 example problems. I believe these 3 example problems help you understand how the coefficient of friction is the key parameter for every object when it is subjected to motion with respect to another body.

Why don’t you solve an example problem yourself and let us know what you get in the comment section below?

Problem statement 4: Block A weighing 1000 N and block B weighing 500 N are connected by flexible wire. The coefficient of friction between block A and the plane is 0.5 while that for block B and the plane is 0.2. Determine what value of inclination of the plane the system will have the impending motion down the plane?

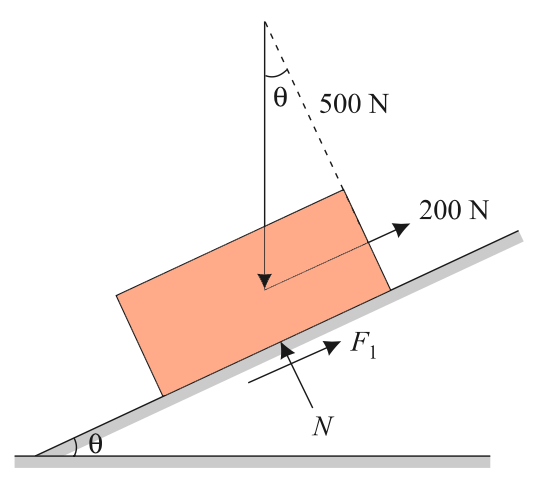
Solve this and let us know if you need any help in the comment section below. Post your answer.