The belts or ropes are used to transmit power from one shaft to another by means of pulleys that rotate at the same speed or at different speeds. The material used for belts and ropes must be strong, flexible, and durable. It must have a high coefficient of friction. Let us see How we can calculate Power Transmitted by a Belt.

Power Transmitted by a Belt
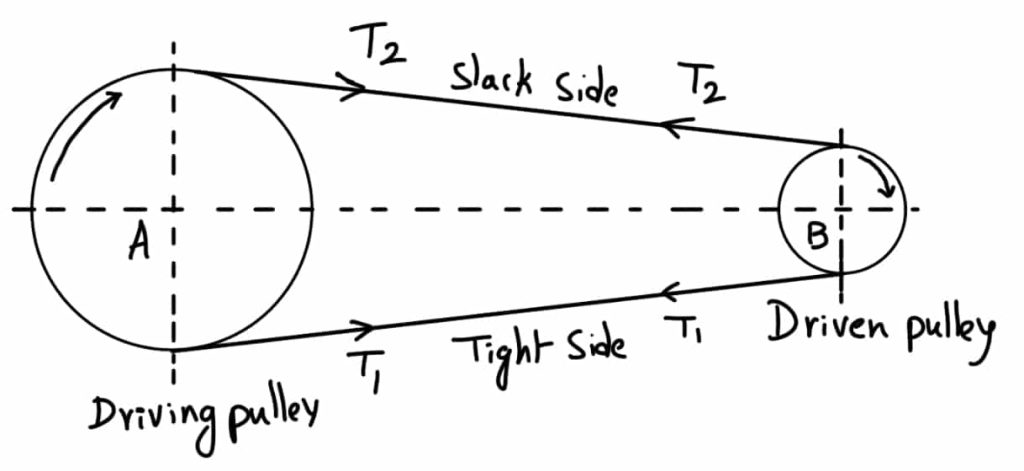
The driving pulley pulls the belt from one side and delivers it to the other side. It is thus obvious that the tension on the former side (i.e., the tight side) will be greater than the latter side (i.e. slack side) as shown in the following figure.
The following figure shows the driving pulley (or driver) A and the driven pulley (or follower) B.
Let
T1 and T2 = Tensions in the tight side and slack side of the belt respectively in Newton
r1 and r2 = Radii of the driving and driven pulleys respectively in meters
ν = Velocity of the belt in m/s.
The effective turning (driving) force at the circumference of the driven pulley or follower is the difference between the two tensions (i.e. T1 – T2).
Work done per second = (T1 – T2) ν N-m/s
Power transmitted = (T1 – T2) ν W
A little consideration will show that torque exerted on the driving pulley is (T1 – T2) r1.
Similarly, the torque exerted on the driven pulley is (T1 – T2) r1.
Ratio of Driving Tensions for Flat Belt Drive
Consider a driven pulley rotating in the clockwise direction as shown in the following figure.
Let
T1 = Tension in the belt on the tight side,
T2 = Tension in the belt on the slack side, and
θ = Angle of contact in radians (i.e. angle subtended by the arc AB, along which the belt touches the pulley, at the center).
Now consider a small portion of the belt PQ, subtending an angle δθ at the center of the pulley as shown in the following figure.
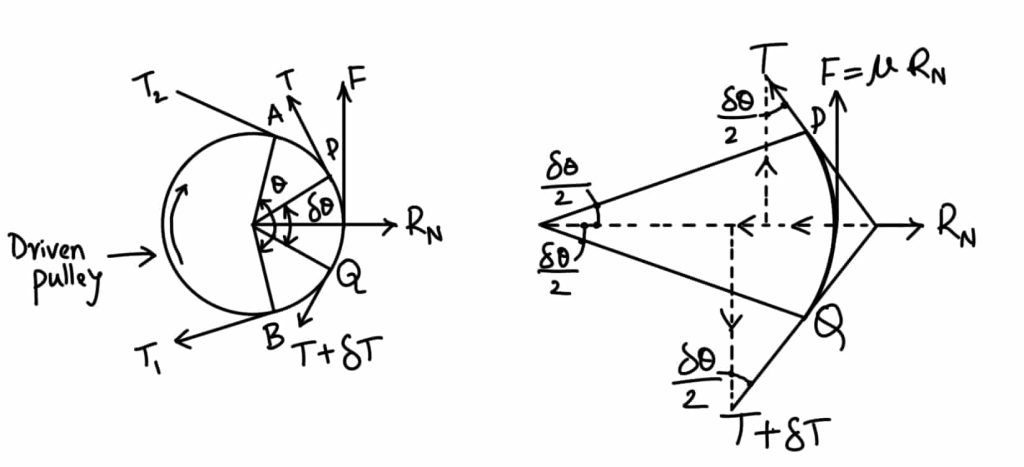
The belt PQ is in equilibrium under the following forces:
- Tension T in the belt at P
- Tension (T+δT) in the belt at Q
- Normal reaction RN
- The frictional force F = μ × RN
where μ is the coefficient of friction between the belt and pulley.
Resolving all the forces horizontally, we have
RN = (T + δT) sin (δT/2) + T sin (δT/2)
Since the angle δθ is very small, therefore putting sin δθ/2 = δθ/2 in the above equation, we have
RN = (T + δT) δθ/2 + T δθ/2
RN = (T × δθ/2) + (δT × δθ/2) + T δθ/2
RN = T × δθ + (δT × δθ/2)
RN = T × δθ … neglecting (δT × δθ/2)
Now resolving the forces vertically, we have
μ × RN = (T + δT) cos (δT/2) – T cos (δT/2)
Since the angle δθ is very small, therefore putting cos δθ/2 = 1 in the above equation, we have
μ × RN = (T + δT) – T
μ × RN = δT
RN = δT / μ
Equating the values of RN from the above equations, we get
T × δθ = δT / μ
μ δθ = δT / T
Integrating the above equation between the limits T2 and T1 and from 0 to θ, we have
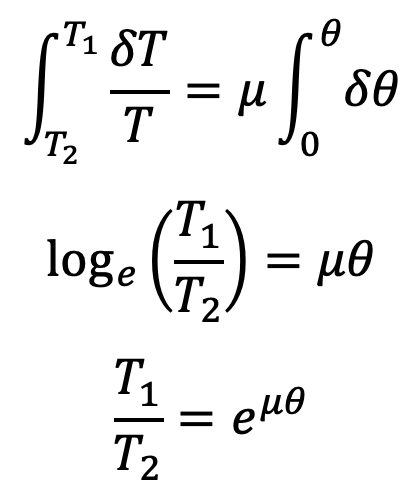
This equation can be further expressed in terms of the corresponding logarithm to the base 10, i.e.
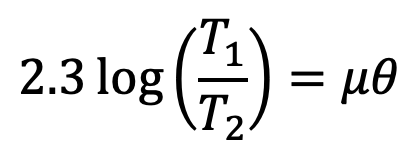
The above expression gives the relation between the tight side and slack side tensions, in terms of coefficient of friction and the angle of contact.
Notes: 1. While determining the angle of contact, it must be remembered that it is the angle of contact at the smaller pulley, if both the pulleys are of the same material. We know that
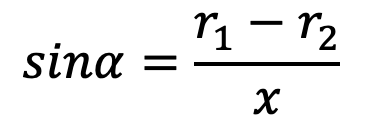
…. for open belt drive
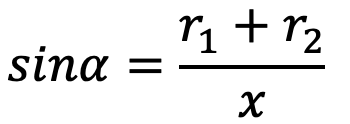
…. for cross-belt drive
The angle of contact or lap,
θ = (180° – 2α) π/180 rad
…. for open belt drive
θ = (180° + 2α) π/180 rad
…. for cross-belt drive
2. When the pulleys are made of different materials (i.e. when the coefficient of friction of the pulleys or the angle of contact are different), then the design will refer to the pulley for which μ.θ is small.
Example Problem on Power Transmitted by a Belt
Problem Statement: Two pulleys, one 450 mm diameter, and the other 200 mm diameter, on parallel shafts 1.95 m apart are connected by a crossed belt.
What power can be transmitted by the belt when the larger pulley rotates at 200 rev/min, if the maximum permissible tension in the belt is 1 kN, and the coefficient of friction between the belt and pulley is 0.25?
Answer:
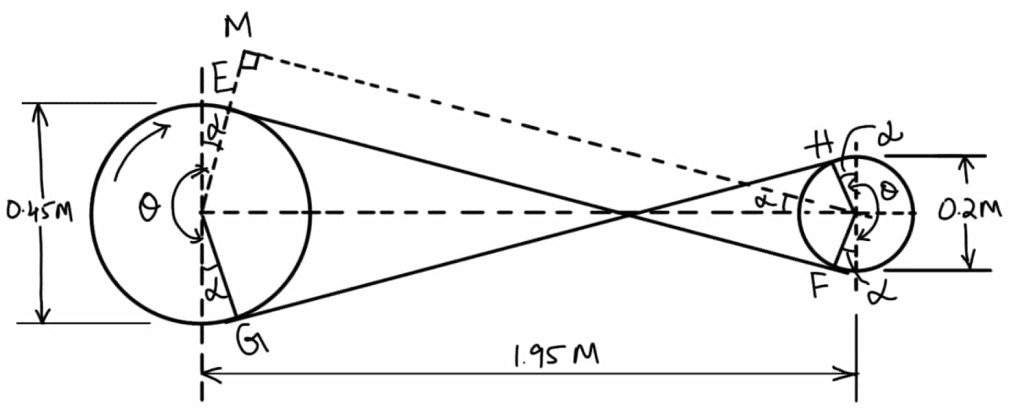
The bigger pully diameter d1 = 450mm = 0.45m or r1 = 0.225m
The smaller pully diameter d2 = 200mm = 0.2m or r2 =0.1m
distance between parallel shafts x = 1.95m
speed of the pully N1 = 200r.p.m
tension in the belt T1 = 1kN = 1000N
Coefficient of friction μ = 0.25
Length of the belt
In relation to finding the length of the belt,
L = π(r1 +r2) + 2x + (r1 + r2)2/x
L = π(0.225+0.1) + 2×1.95 + (0.225 + 0.1)2/1.95
L = 1.02 + 3.9 + 0.054
L = 4.974m
The angle of contact between the belt and each pulley
Let θ = Angle of contact between the belt and each pulley.
We know that for a crossed-belt drive
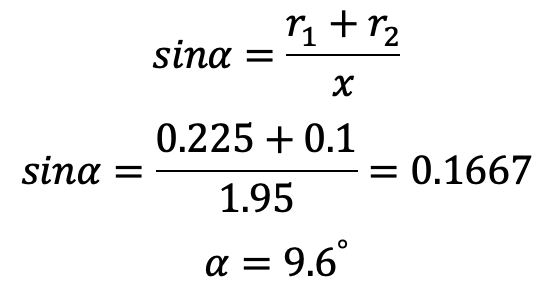
and,
θ = (180° + 2α) = 180 + 2 × 9.6 = 199.2°
θ = (π/180) × 199.2 = 3.477 rad
Power Transmitted by a Belt
Let
T1 = Tension in the belt on the tight side,
T2 = Tension in the belt on the slack side, and
we know from the above
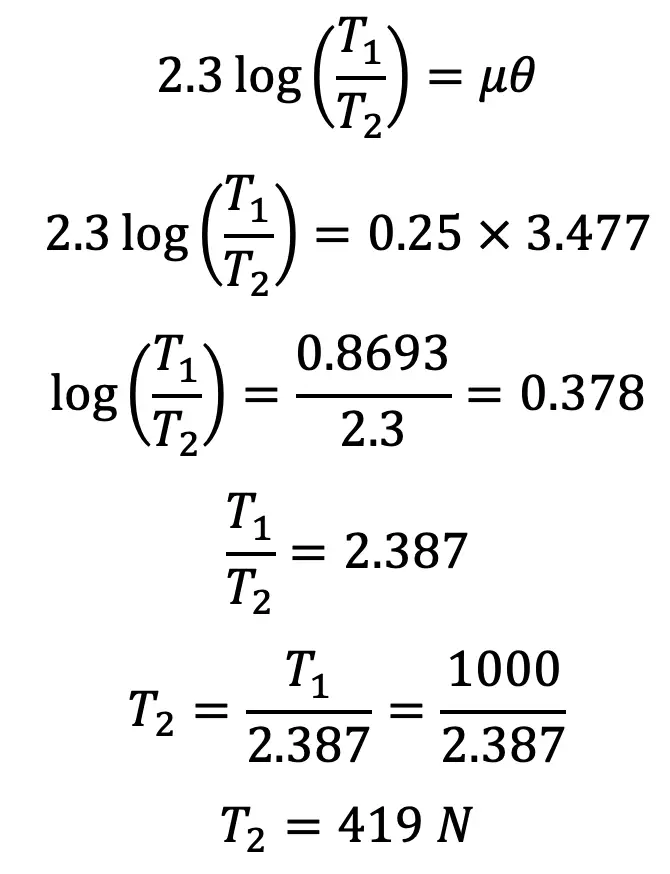
We know that the velocity of the belt,
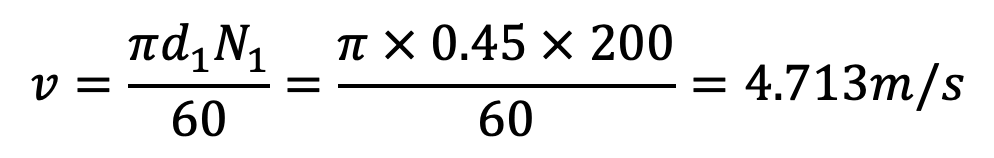
∴ Power transmitted,
P = (T1 –T2)v = (1000 – 419) × 4.713
P = 2738 W = 2.738 kW
The Power Transmitted by the given Belt is 2.738 kW.
This is all about how you can calculate the Power Transmitted by a Belt. Let us know what you think about this article in the comment section below.

Leave a Reply