A Nozzle is the portion of the pipe where the cross-sectional area varies from larger diameter to smaller diameter, and it can be used to direct or modify the flow of a fluid. A jet is a liquid stream projected into a surrounding medium or an object from the nozzle. This article will discuss How we can Calculate Force Exerted by a Jet on a Series of curved Vanes. This principle is used in the design of turbines, centrifugal pumps, impellers and propellers.

The liquid comes out in the form of a jet from the outlet of a nozzle, which is fitted to a pipe through which the liquid is flowing under pressure. If some plate, which may be fixed or moving, is placed in the path of the jet, a force is exerted by the jet on the plate. This force is obtained from Newton’s second law of motion or from the impulse-momentum equation. Thus the impact of a jet means the force exerted by the jet on a plate which may be stationary or moving. In the previous article, we have discussed the following.
- How to Calculate Force Exerted by Jet on Stationary Objects
- How to Calculate Force Exerted by Jet on Moving Object
Force Exerted by a Jet on a Series of Vanes
The force exerted by a jet of water on a single moving plate (which may be flat or curved) is not practically feasible. This case is only a theoretical one. In actual practice, a large number of plates are mounted on the circumference of a wheel at a fixed distance apart as shown in the following figure.
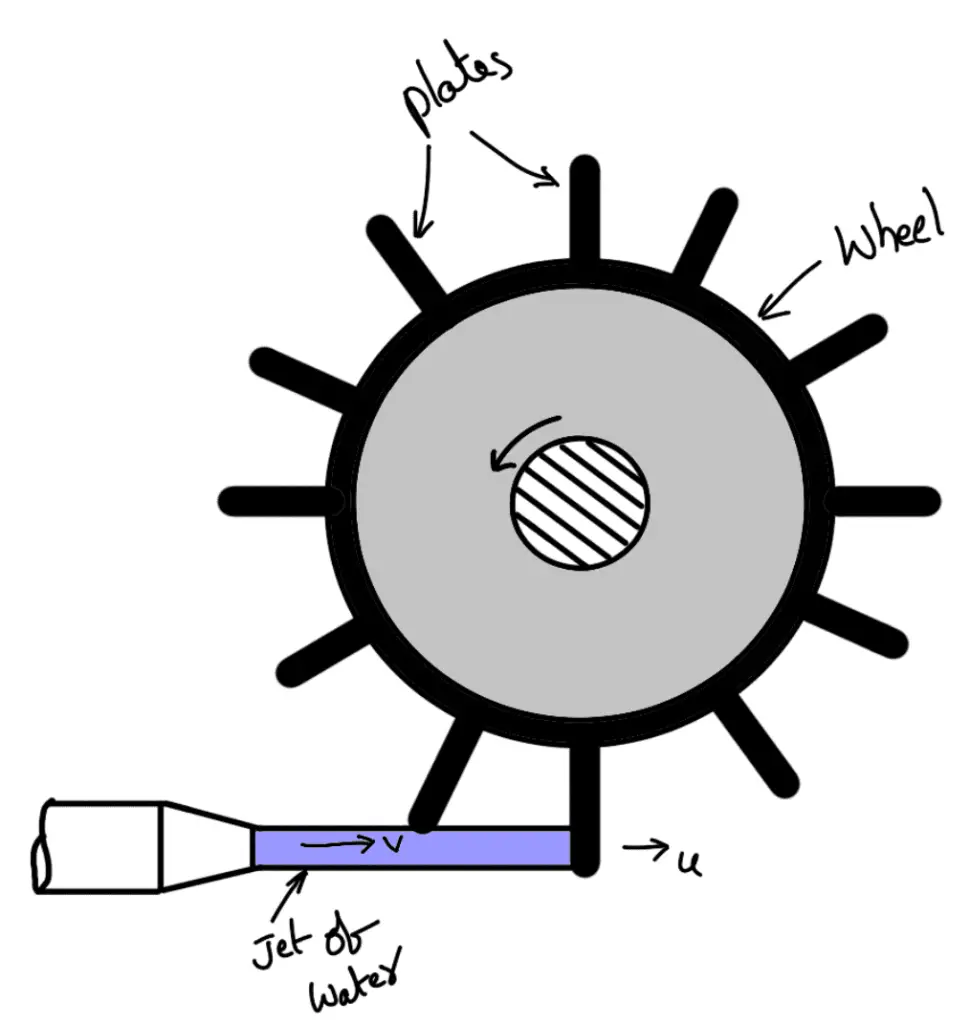
The jet strikes a plate and due to the force exerted by the jet on the plate, the wheel starts moving and the 2nd plate mounted on the wheel appears before the jet, which again exerts the force on the 2nd plate. Thus each plate appears successively before the jet and the jet exerts a force on each plate. The wheel starts moving at a constant speed.
Let
V = Velocity of jet
d = Diameter of jet
a = Cross-sectional area of jet = (π/4)d2
u = Velocity of the vane
In this case, the mass of water coming out from the nozzle per second is always in contact with the plates, when all the plates are considered. Hence
The mass of water per second striking the series of plates = ρaV
Also, the jet strikes the plate with a velocity = (V – u).
After striking, the jet moves tangential to the plate and hence the velocity component in the direction of motion of the plate is equal to zero.
The force exerted by the jet in the direction of motion of the plate,
Fx = Mass per second [Initial velocity – Final velocity]
Fx = ρaV[(V – u) – 0]
Fx= ρaV[V – u]
Work done by the jet on the series of plates per second = Force × Distance per second in the direction of force
W = Fx × u
W = ρaV[V – u] × u
The kinetic energy of the jet per second can be written as
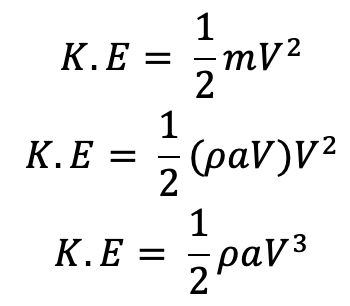
The Efficiency we can write
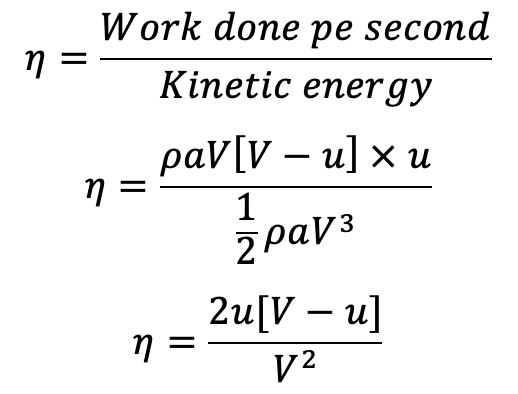
Condition for Maximum Efficiency
The above Equation (a) gives the value of the efficiency of the wheel. For a given jet velocity V, the efficiency will be maximum when
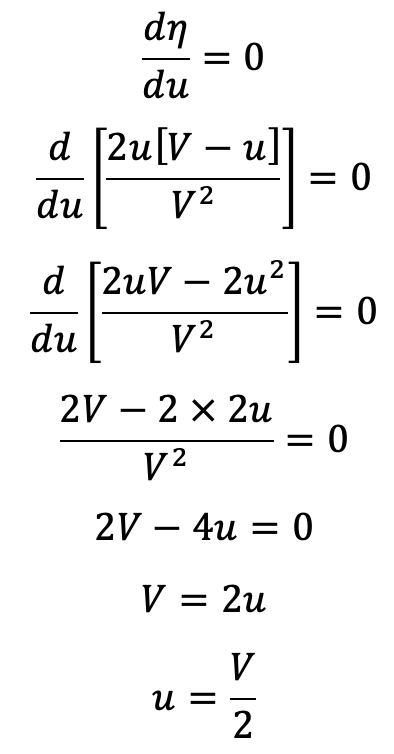
Maximum Efficiency
Substituting the value of V = 2u in equation (a), we get the maximum efficiency as
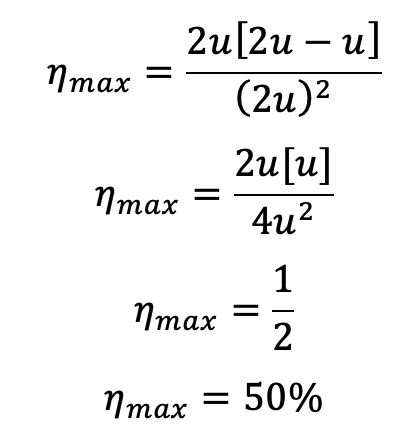
Force Exerted on a Series of Curved Vanes
For a radial curved vane, the radius of the vane at the inlet and outlet is different and hence the tangential velocities of the radial vane at the inlet and outlet will not be equal. Consider a series of radial curved vanes mounted on a wheel as shown in the following figure. The jet of water strikes the vanes and the wheel starts rotating at a constant angular speed.
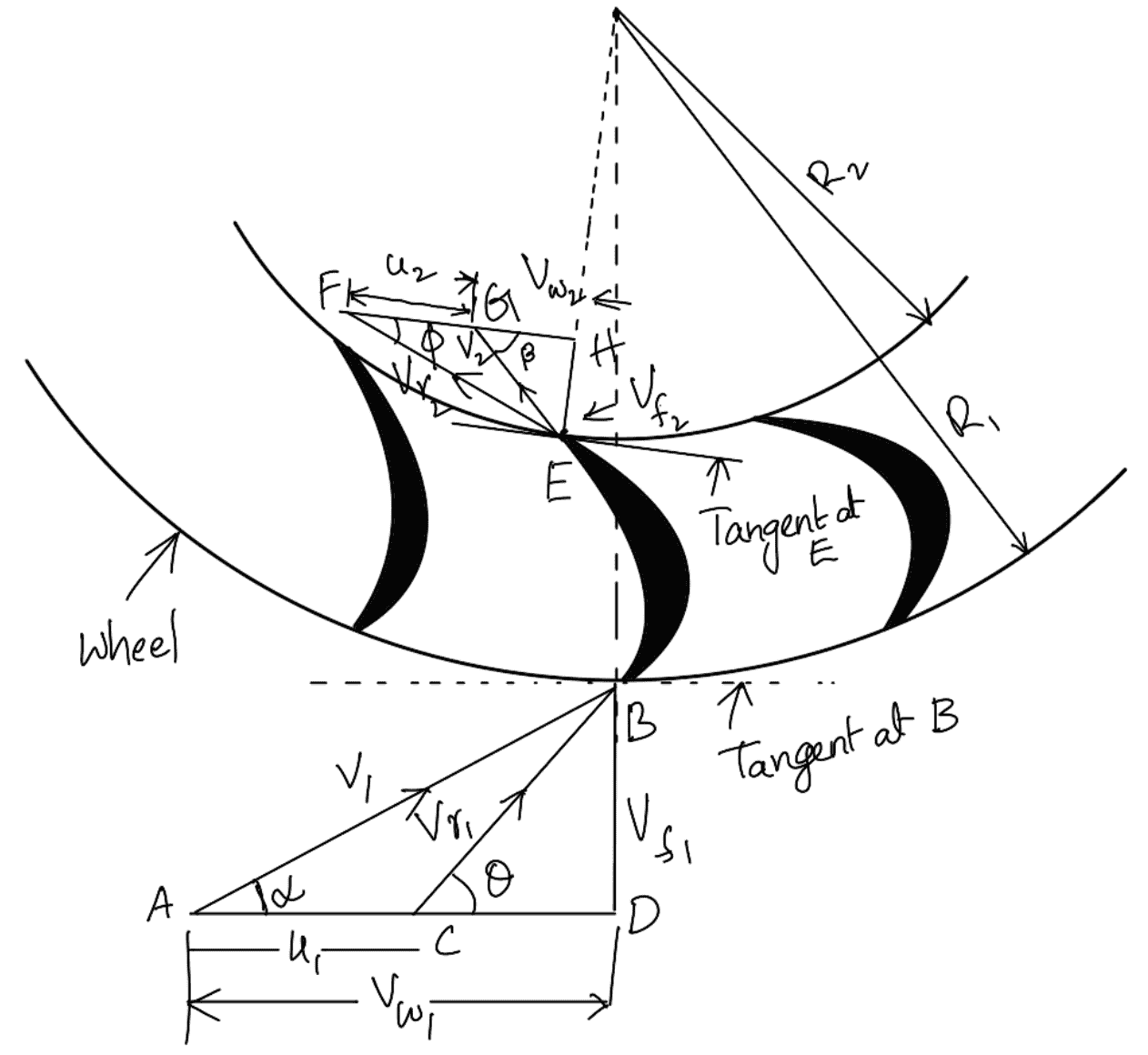
R1 = Radius of the wheel at the inlet of the vane
R2 = Radius of the wheel at the outlet of the vane
ω = Angular speed of the wheel
Then
u1 = ωR1
u2 = ωR2
The velocity triangles at the inlet and outlet are drawn as shown in the above figure.
The mass of water striking per second for a series of vanes
= Mass of water coming out from nozzle per second
= ρaV1
where
a = Area of jet and
V1 = Velocity of jet
The momentum of water striking the vanes in the tangential direction per sec at the inlet
= Mass of water per second × Component of V1 in the tangential direction
= ρaV1 × Vw1
(Component of V1 in tangential direction = V1 cos 𝝰 = Vw1)
Similarly, the momentum of water at the outlet per sec
= ρaV1 × Component of V2 in the tangential direction
= ρaV1 × (- V2 cos 𝝱)
= – ρaV1 × Vw2
(-ve sign is taken as the velocity V2 at the outlet is in the opposite direction.)
Now, angular momentum per second at the inlet = Momentum at the inlet × Radius at the inlet
= ρaV1 × Vw1 × R1
Angular momentum per second at outlet = Momentum of outlet x Radius at the outlet
= – ρaV1 × Vw2 × R2
The torque exerted by the water on the wheel,
T = Rate of change of angular momentum
T = [Initial angular momentum per second – Final angular momentum per second]
T = ρaV1 × Vw1 × R1 – (- ρaV1 × Vw2 × R2)
T = ρaV1 (Vw1 × R1 + Vw2 × R2)
Work done per second on the wheel
W = Torque × Angular velocity
W = T × ω
W = ρaV1 (Vw1 × R1 + Vw2 × R2) × ω
W = ρaV1 (Vw1 × R1 × ω + Vw2 × R2 × ω)
W = ρaV1 (Vw1 u1 + Vw2 u2)
If the angle 𝝱 in the above series of curved vanes figure is an obtuse angle then work done per second will be given as
W = ρaV1 (Vw1 u1 + Vw2 u2)
The general expression for the work done per second on the wheel
W = ρaV1 (Vw1 u1 ± Vw2 u2)
If the discharge is radial at the outlet, then 𝝱 = 90° and the work done becomes as
W = ρaV1 (Vw1 u1)
Efficiency of the Radial Curved Vane
The work done per second on the wheel is the output of the system whereas the initial kinetic energy per second of the jet is the input. Hence, the efficiency of the system is expressed as
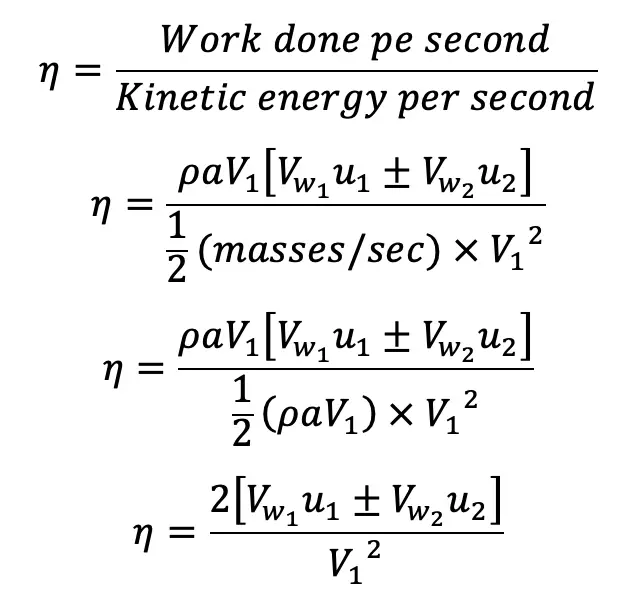
If there is no loss of energy when water is flowing over the vanes, the work done on the wheel per second is also equal to the change in kinetic energy of the jet per second. Hence, the work done per second on the wheel is also given as
Work done per second on the wheel = Change of K.E. per second of the jet
W = (Initial K.E. per second – Final K.E. per second) of the jet
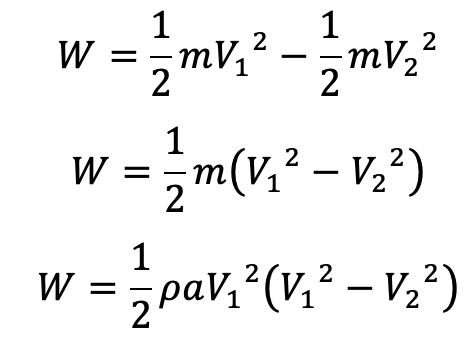
Hence efficiency relation we can write

From the above equation, it is clear that for a given initial velocity of the jet (i.e., V1), the efficiency will be maximum when V2 is minimum. But V2 can not be zero as in that case the incoming jet will not move out of the vane. Equation (d) also gives the efficiency of the system.
From this equation, it is clear that efficiency will be maximum when Vw2 is added to Vw1. This is only possible if 𝝱 is an acute angle.
Also for maximum efficiency, Vw2 should also be maximum. This is only possible if 𝝱 = 0.
In that case, Vw2 = V2 and angle φ will be zero.
But in actual practice φ cannot be zero. Hence for maximum efficiency, the angle φ should be minimum.
This is all about determining the Force Exerted by a Jet on a Series of flat Vanes and curved vanes.
Let us solve an example problem to calculate the Force Exerted by a Jet on a series of curved vanes.
Example Problems to calculate the Force Exerted by a Jet on a series of Curved Vanes
Problem Statement: A jet of water having a velocity of 35 m/s impinges on a series of vanes moving with a velocity of 20 m/s. The jet makes an angle of 30° to the direction of motion of vanes when entering and leaving at an angle of 120°. Draw the triangles of velocities at the inlet and outlet and find :
(a) Angles of vanes tips so that water enters and leaves without shock
(b) Work done per unit weight of water entering the vanes
(c) Efficiency
Answer:
Given data
The velocity of jet, V1 = 35 m/s
The velocity of the vane, u1 = u2 = 20 m/s
The angle of the jet at the inlet, α = 30°
Angle made by the jet at the outlet with the direction of motion of vanes = 120°
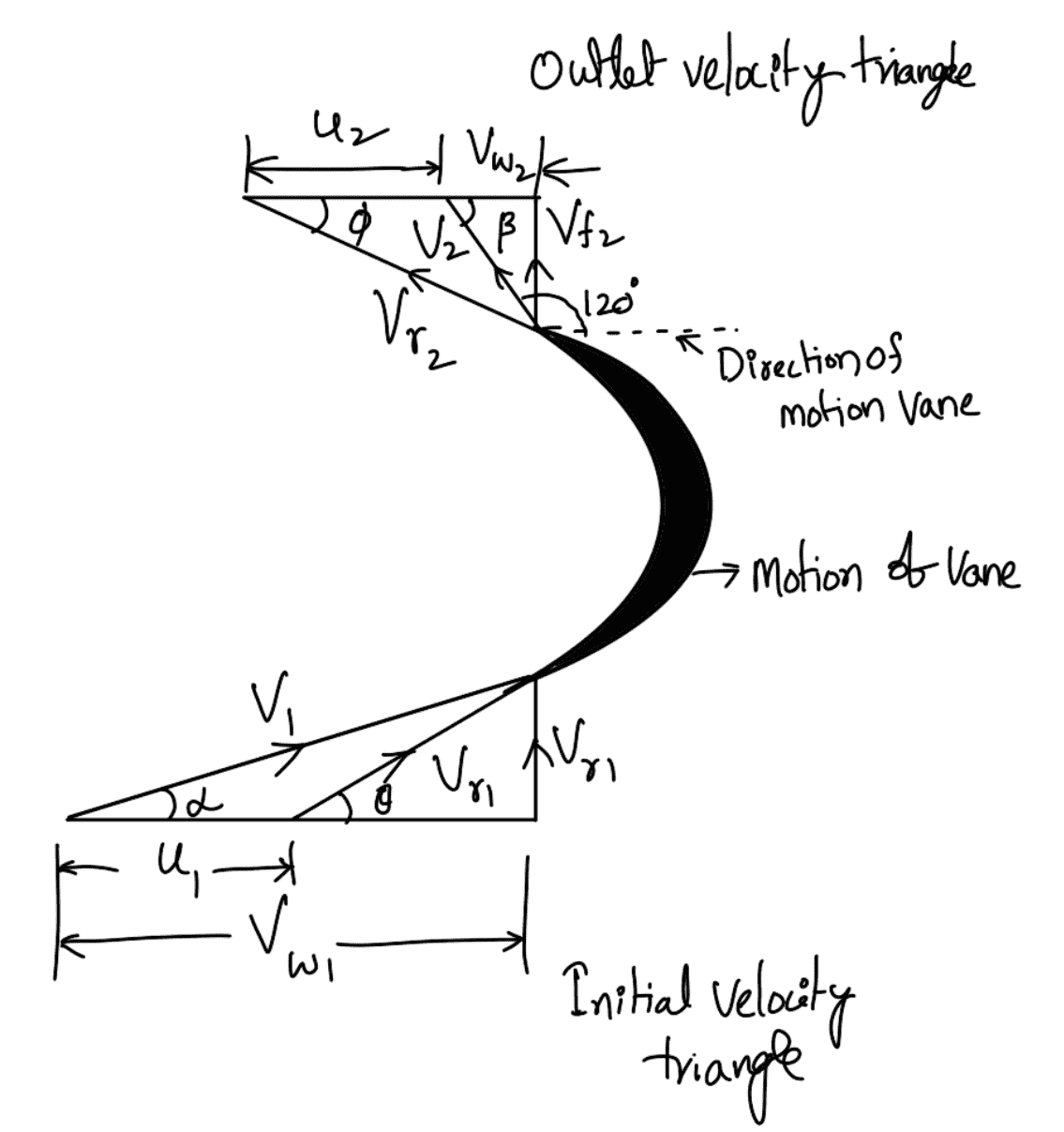
Angle ß = 180° – 120° = 60°
(a) Angles of vanes tips
From inlet velocity triangle
Vw1 = V1 cos α = 35 cos 30° = 30.31 m/s
Vf1 = V1 sin α = 35 sin 30° = 17.50 m/s
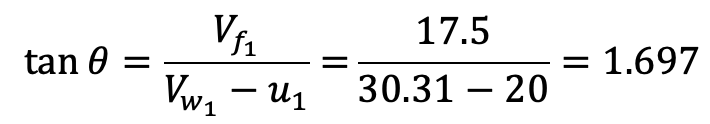
θ = tan -1 1.697 = 60°
By sine rule,
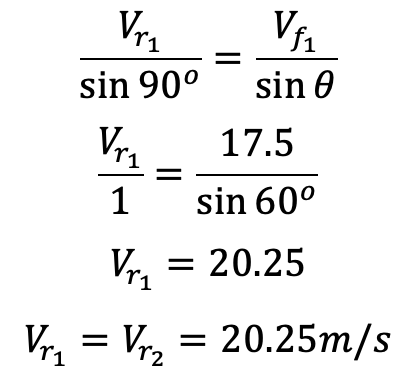
From the outlet velocity triangle, by the sine rule
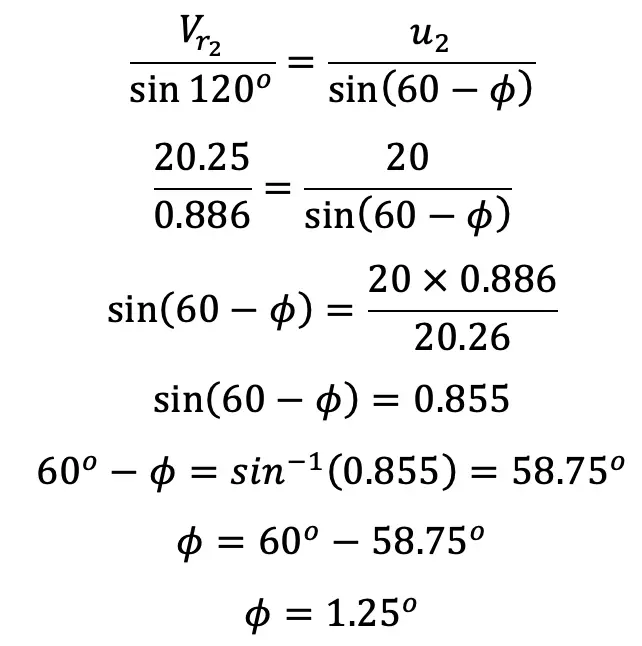
(b) Work done
The Work done per unit weight of water entering the vanes = (1/g) (Vw1 + Vw2) × u1
Vw1 = 30.31 m/s and u1 = 30 m/s
The value of Vw2 is obtained from the outlet velocity triangle
Vw2 = Vr2 cos φ – u2
Vw2 = 20.25 cos 1.25° – 20.0
Vw2 = 0.24 m/s
Work done/unit weight = (1/9.81) (30.31 + 0.24) × 20 = 62.28
(c) Efficiency
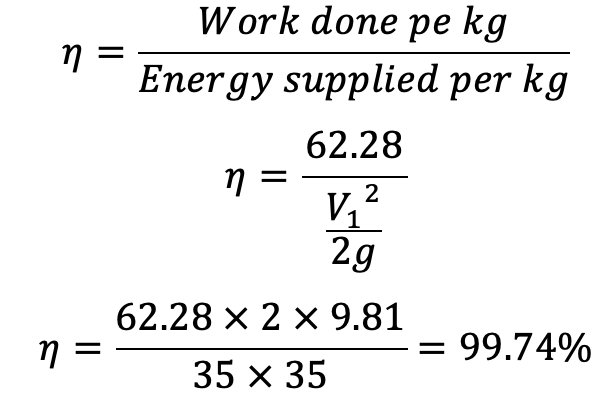
This is how we can calculate the Force Exerted by a Jet on a series of Curved Vanes. Let us know what you think about this article in the comment section below.

Leave a Reply