How to Calculate Force Exerted by Jet on Moving Object?

A Nozzle is the portion of the pipe where the cross-sectional area varies from larger diameter to smaller diameter, and it can be used to direct or modify the flow of a fluid. A jet is a liquid stream projected into a surrounding medium or an object from the nozzle. In this article, we will discuss the force exerted by Jet on Stationary objects.

The liquid comes out in the form of a jet from the outlet of a nozzle, which is fitted to a pipe through which the liquid is flowing under pressure. If some plate, which may be fixed or moving, is placed in the path of the jet, a force is exerted by the jet on the plate. This force is obtained from Newton’s second law of motion or from the impulse-momentum equation. Thus the impact of a jet means the force exerted by the jet on a plate which may be stationary or moving. Following are the cases of the impact of a jet i.e., the force exerted by the jet on a plate, will be considered

Force Exerted by the Jet on a stationary plate when

• The plate is vertical to the jet
• The plate is inclined to the jet
• The plate is curved

Force Exerted by the Jet on a moving plate, when

• The plate is vertical to the jet
• The plate is inclined to the jet
• The plate is curved

Force Exerted By A Jet On Moving Plates

The following cases of the moving plates will be considered :

1. A flat vertical plate moving in the direction of the jet and away from the jet
2. Inclined plate moving in the direction of the jet
3. Curved plate moving in the direction of the jet or in the horizontal direction

1. Force on Flat Vertical Plate Moving in the Direction of Jet

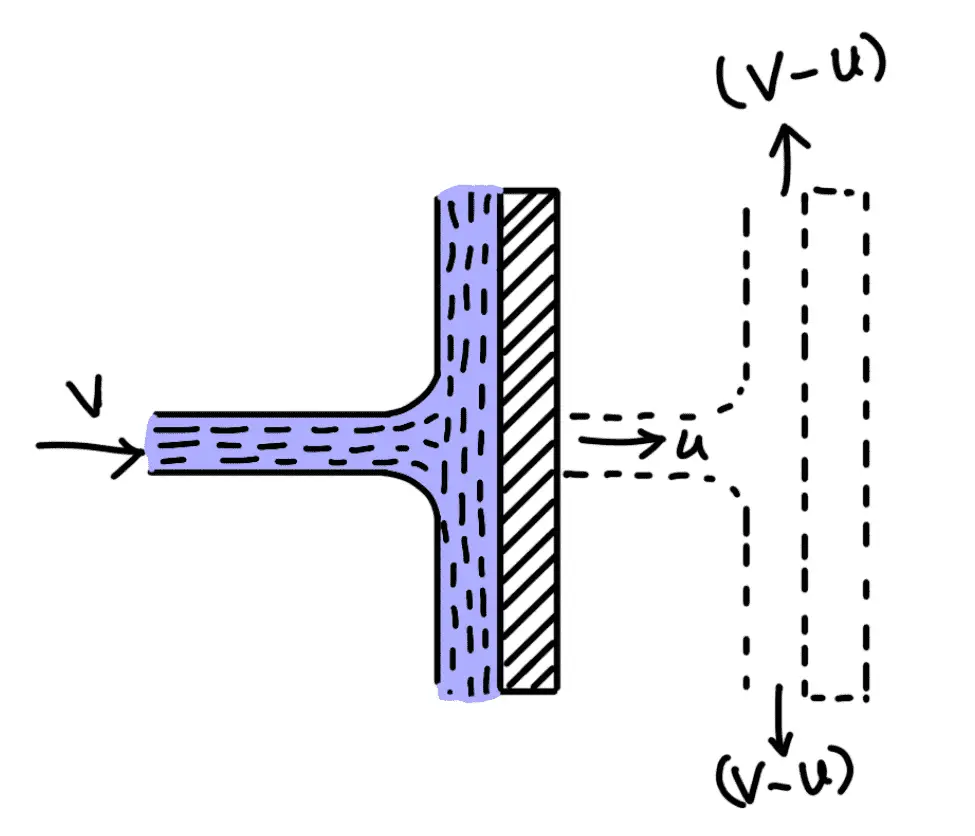
The following figure shows a jet of water striking a flat vertical plate moving with a uniform velocity away from the jet.

Let
V = Velocity of the jet (absolute)
a = Area of the cross-section of the jet
u = Velocity of the flat plate

In this case, the jet does not strike the plate with a velocity V, but it strikes with a relative velocity, which is equal to the absolute velocity of the jet of water minus the velocity of the plate.

Hence relative velocity of the jet with respect to plate = (V – u)

Mass of water striking the plate per sec = ρ × Area of jet × Velocity with which jet strikes the plate

= ρ a × [V – u]

Force exerted by the jet on the moving plate in the direction of the jet

F_x = Mass of water striking per sec × [Initial velocity with which water strikes – Final velocity]

F_x = ρa(V – u) × [(V – u)-0]

F_x = ρa(V – u)²

In this case, the work will be done by the jet on the plate, as the plate is moving. For the stationary plates, the work done is zero.

Work done per second by the jet on the plate = Force × (Distance in the direction of force ÷ Time)

W = F_x × u
W = ρa(V – u)² × u

In the above equation, if the value of ρ for water is taken in S.I. units (i.e., 1000 kg/m³), the work done will be in N m/s. The term Nm/s is equal to W (watt).

2. Force on the Inclined Plate Moving in the Direction of the Jet

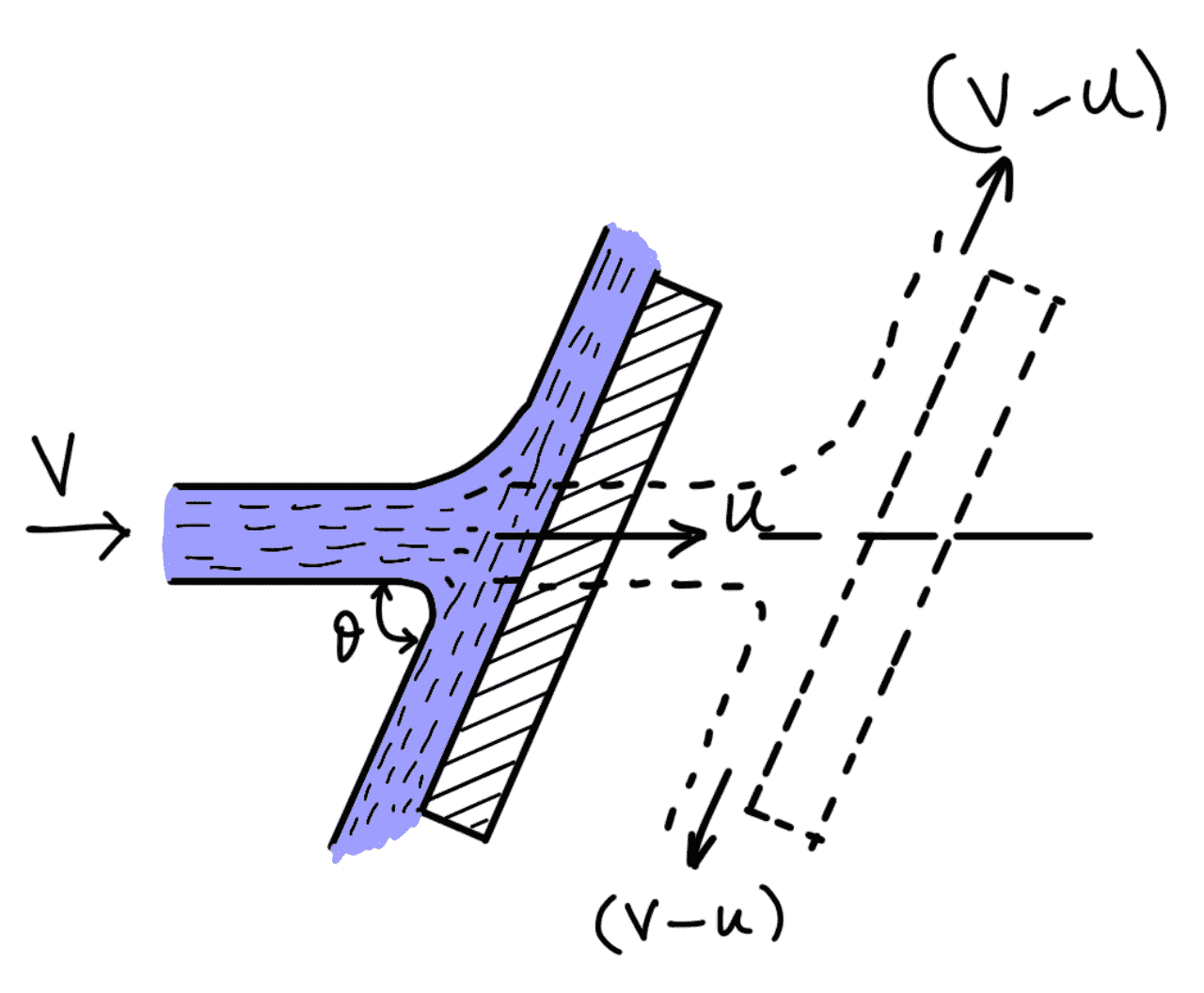
Let a jet of water strikes an inclined plate, which is moving with a uniform velocity in the direction of the jet as shown in the following figure.

Let
V = Absolute velocity of the jet of water,
u = Velocity of the plate in the direction of jet,
a = Cross-sectional area of jet
θ = Angle between jet and plate

The relative velocity of the jet of water = (V – u)

The velocity with which jet strikes = (V – u)

Mass of water striking per second = ρ × a × (V – u)

If the plate is smooth and the loss of energy due to the impact of the jet is assumed zero, the jet of water will leave the inclined plate with a velocity equal to (V- u).

The force exerted by the jet of water on the plate in the direction normal to the plate is given as

F_n = Mass striking per second × [Initial velocity in the normal direction with which jet strikes – Final velocity]

F_n = ρa (V – u) [(V – u) sin θ – 0]
F_n = ρa (V – u)² sin θ

This normal force F_n is resolved into two components namely F_x and F_y in the direction of the jet and perpendicular to the direction of the jet respectively.

F_x = F_n sin θ
F_x = ρa (V – u)² sin² θ

F_y = F_n cos θ
F_y = ρa (V – u)² sin θ cos θ

Work done per second by the jet on the plate = F_x × Distance per second in the direction of x

W = F_x × u
W = ρa (V – u)² sin² θ × u
W = ρa u (V – u)² sin² θ N m/s

3. Force on the Curved Plate when the Plate is Moving in the Direction of Jet

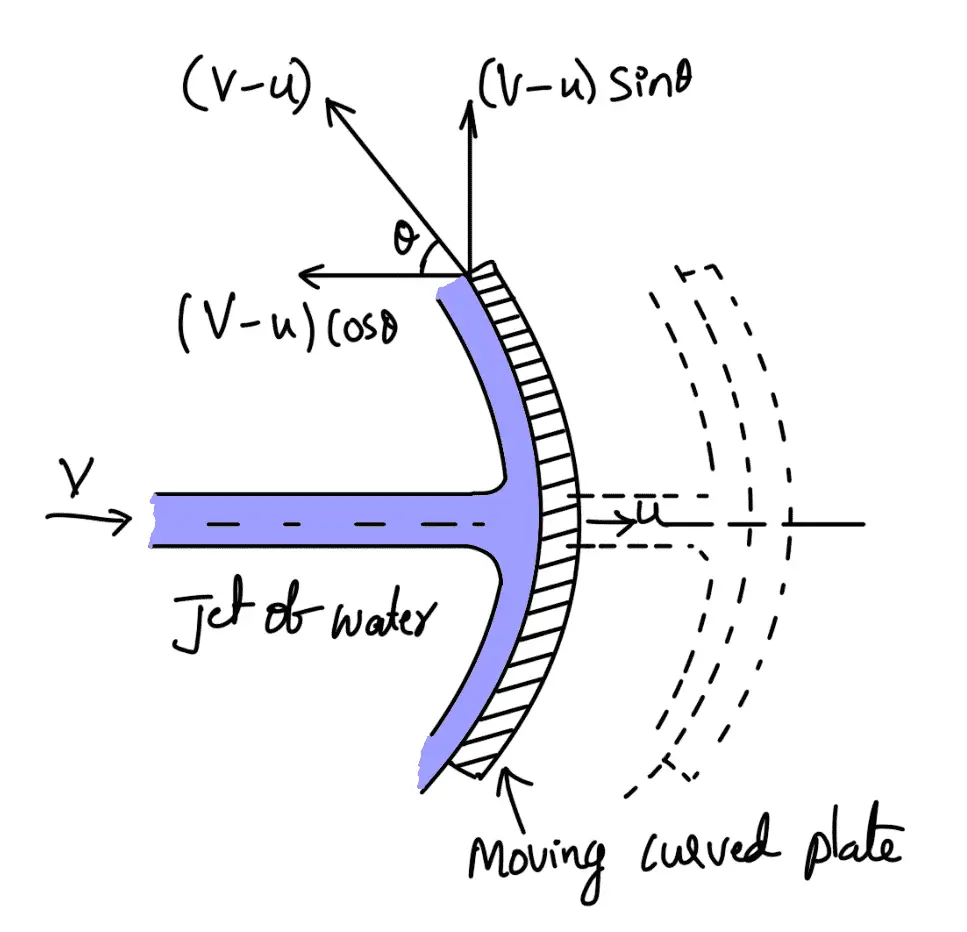
Let a jet of water strikes a curved plate at the centre of the plate which is moving with a uniform velocity in the direction of the jet as shown in the following figure.

Let
V = Absolute velocity of the jet
a = Area of jet
u = Velocity of the plate in the direction of the jet

The relative velocity of the jet of water or the velocity with which the jet strikes the curved plate = (V – u).

If the plate is smooth and the loss of energy due to the impact of the jet is zero, then the velocity with which the jet will be leaving the curved vane = (V – u)

This velocity can be resolved into two components, one in the direction of the jet and another perpendicular to the direction of the jet.

Component of the velocity in the direction of jet = -(V – u) cos A

(-ve sign is taken as at the outlet, the component is in the opposite direction of the jet).

Component of the velocity in the direction perpendicular to the direction of the jet = (V – u) sin θ

Mass of the water striking the plate = ρ × a × Velocity with which jet strikes the plate

= ρa(V – u)

Force exerted by the jet of water on the curved plate in the direction of the jet,

F_x = Mass striking per sec × [Initial velocity with which jet strikes the plate in the direction of jet – Final velocity]

F_x = ρa(V – u) [(V – u) – (- (V – u) cos θ )]
F_x = ρa(V – u) [(V – u) + (V – u) cos θ]
F_x = ρa(V – u)² [1 + cos θ]

Work done by the jet on the plate per second
W = F_x × Distance travelled per second in the direction of x
W = F_x × u
W = ρa(V – u)² [1 + cos 0 ] × u
W = ρa(V – u)² × u [1 + cos θ]

Example Problems

Let us solve an example to Calculate Force Exerted by Jet on Moving Object.

Problem Statement: A jet of water of diameter 7.5 cm strikes a curved plate at its centre with a velocity of 20 m/s. The curved plate is moving with a velocity of 8 m/s in the direction of the jet. The jet is deflected through an angle of 165°. Assuming the plate smooth find the following
(i) Force exerted on the plate in the direction of the jet
(ii) Power of the jet
(ii) Efficiency of the jet

Answer:

Given data
Diameter of the jet, d = 7.5 cm = 0.075 m
Area, a = (π/4) (0.075)² = 0.004417
The velocity of the jet, V = 20 m/s
The velocity of the plate, u = 8 m/s
The angle of deflection of the jet, = 165°

Angle made by the relative velocity at the outlet of the plate, θ = 180°- 165° = 15°

(i) Force exerted by the jet on the plate in the direction of the jet

Force exerted by the jet on the plate in the direction of the jet is given by the equation derived above as

F_x = ρa(V – u)² [1 + cos θ]
F_x = 1000 × 0.004417 × (20 – 8)2 [1 + cos 15°]
F_x = 1250.38 N

(ii) Work done by the jet on the plate

Work done by the jet on the plate per second

W = F_x × u = 1250.38 × 8 = 10003.04 N m/s

Power of the jet = 10003.04 / 1000 = 10 kW

(iii) Efficiency of the Jet

The Efficiency of the jet

The Efficiency of the jet is 56%.

This is how you can calculate the Calculate Force Exerted by Jet on Moving Object and also the work done and the efficiency also can be calculated. let us know what you think about this article in the comment section below.