Double Block Brake | Double Shoe Brake

A brake is a device by means of which artificial frictional resistance is applied to a moving machine member, in order to retard or stop the motion of a machine. In the process of performing this function, the brake absorbs either the kinetic energy of the moving member or potential energy given up by objects being lowered by hoists, elevators, etc. In the previous articles, we discussed how we can calculate the energy absorbed by a brake and Heat Dissipation during Braking. We also discussed the different types of Brakes in the previous article. Let us discuss the Double Block Brake in detail.

As we mentioned above that the brake is used to retard or stop the motion of a machine. This action is called Braking. In the process of braking, the brake absorbs either the kinetic energy of the moving member or potential energy given up by objects being lowered by hoists, elevators etc. The energy absorbed by brakes is dissipated in the form of heat. This heat is dissipated in the surrounding air (or water which is circulated through the passages in the brake drum) so that excessive heating of the brake lining does not take place.

The design or capacity of a brake depends upon the following factors:

1. The unit pressure between the braking surfaces
2. The coefficient of friction between the braking surfaces
3. The peripheral velocity of the brake drum
4. The projected area of the friction surfaces
5. The ability of the brake to dissipate heat is equivalent to the energy being absorbed.

The major functional difference between a clutch and a brake is that a clutch is used to keep the driving and driven member moving together, whereas brakes are used to stop a moving member or to control its speed.

We also solved an example problem to stop A vehicle of mass 1200 kg is moving down the hill at a slope of 1:5. by finding how much amount of Braking Torque is required to stop the vehicle in the previous article.

Double Block Brake or Double Shoe Brake

When a single block brake is applied to a rolling wheel, an additional load is thrown on the shaft bearings due to the normal force (RN). This produces bending of the shaft. To overcome this drawback, a double block or shoe brake as shown in the following figure is used.

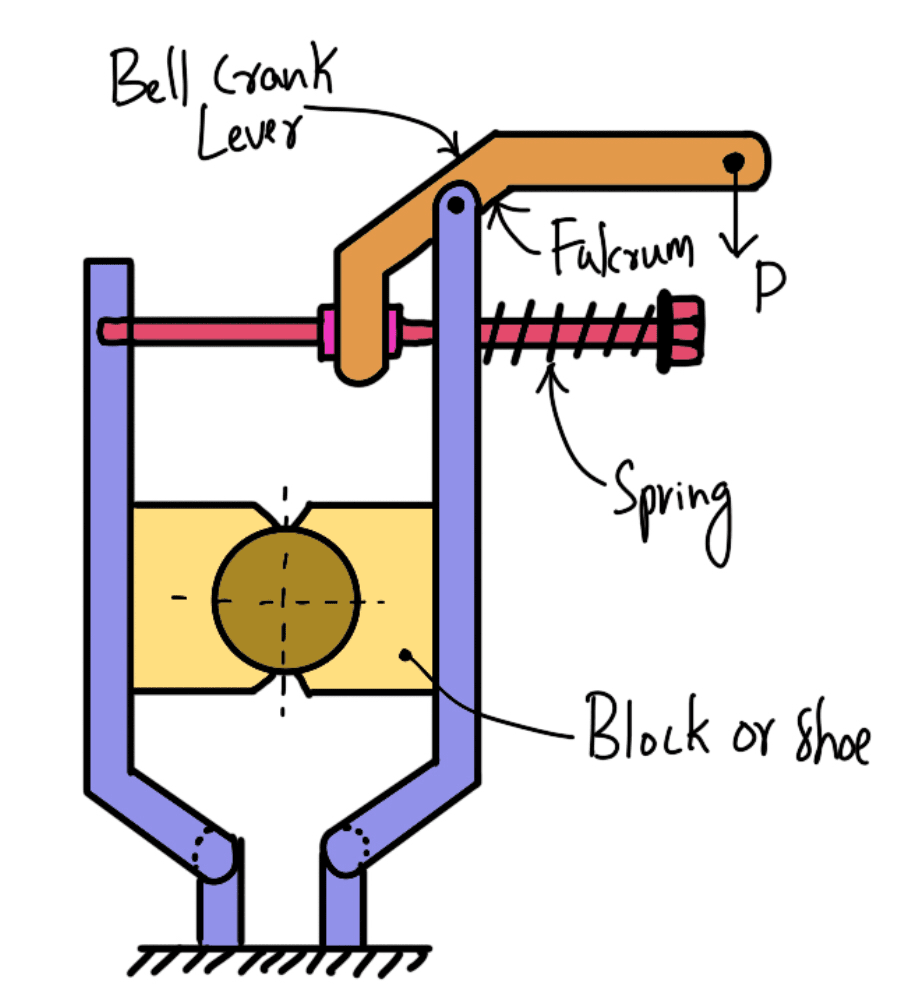
It consists of two brake blocks applied at the opposite ends of a diameter of the wheel which eliminate or reduce the unbalanced force on the shaft.

The brake is set by a spring which pulls the upper ends of the brake arms together. When a force P is applied to the bell crank lever, the spring is compressed and the brake is released.

This type of brake is often used on electric cranes and the force P is produced by an electromagnet or solenoid. When the current is switched off, there is no force on the bell crank lever, and the brake is engaged automatically due to the spring force thus there will be no downward movement of the load.

In a double block brake, the braking action is doubled by the use of two blocks and the two blocks may be operated practically by the same force which will operate one. In case of double block or shoe brake, the braking torque is given by

T_B = (F_t1 + F_t2)r

where F_t1 and F_t2 are the braking forces on the two blocks.

Let us solve an example problem to find the spring force required for braking with Double Block Brake.

Example Problem on Double Block Brake

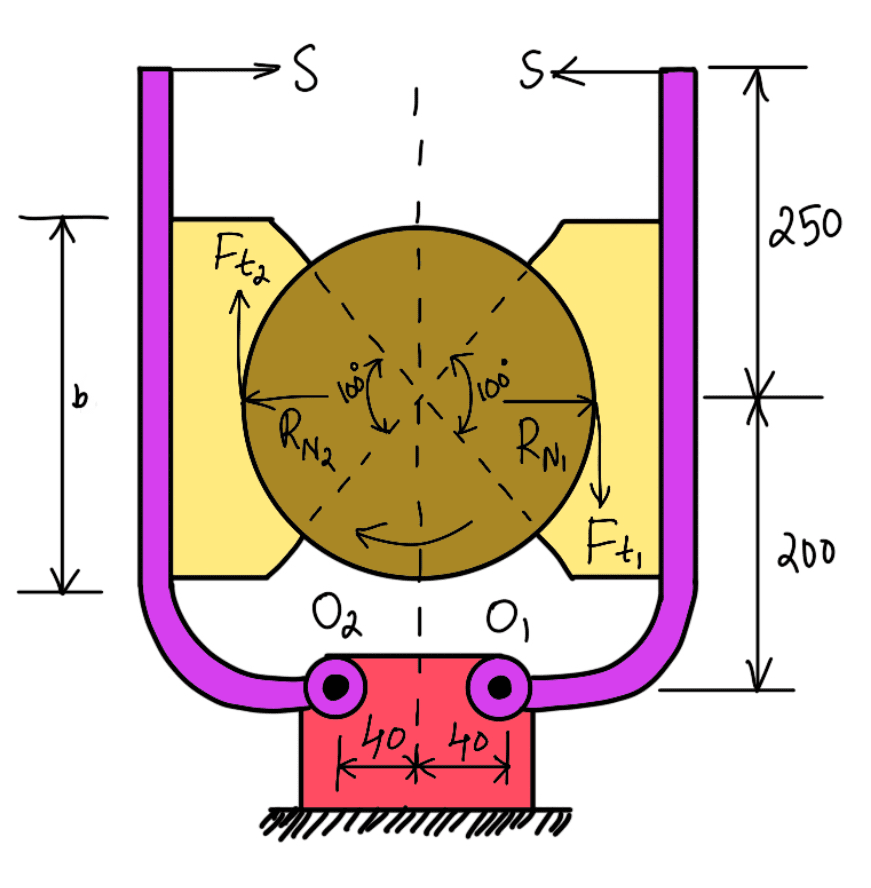
Problem Statement: A double shoe brake, as shown in the following figure is capable of absorbing a torque of 1400 N-m. The diameter of the brake drum is 350 mm and the angle of contact for each shoe is 100°. If the coefficient of friction between the brake drum and lining is 0.4.

Calculate
1. Spring force required for braking with Double Block Brake
2. Width of the brake shoes (if the bearing pressure on the lining material is not to exceed 0.3 N/mm²)

Answer:

Given Data
Braking torque T_B = 1400N-m = 1400×10³ N-mm
Diameter of the Brake Drum d = 350 mm or radius r = 175mm
Angle of the contact surface of the block 2θ = 100° = 100 × π/180 = 1.75 rad
Coefficient of friction μ = 0.4
Bearing pressure on the shoe p_b = 0.3 N/mm²

1. Spring force required for braking with Double Block Brake

S = Spring force necessary to set the brake,
R_N1 and F_t1 = Normal reaction and the braking force on the right-hand side shoe
R_N2 and F_t2 = Corresponding values on the left-hand side shoe.

Since the angle of contact is greater than 60°, therefore equivalent coefficient of friction,

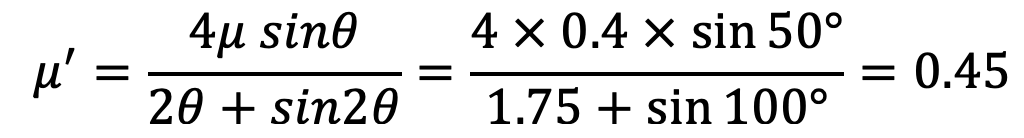
Taking moments about the fulcrum O₁, we have

S × 450 = R_N1 × 200 + F_t1 (175 – 40)
S × 450 = (F_t1 ÷ 0.45) × 200 + F_t1 × 135
S × 450 = 579.4 F_t1
F_t1 = S × 450 ÷ 579.4
F_t1 = 0.776 S

Again taking moments about O₂, we have

S × 450 + F_t2 (175–40) = R_N2 × 200
S × 450 + F_t2 (175–40) = F_t2 ×200
S × 450 + 135 F_t2 = 444.4 F_t2
444.4 F_t2 – 135 F_t2 = S × 450
309.4 F_t2 = S × 450
F_t2 = S × 450 ÷ 309.4
F_t2 = 1.454 S

We know that the Brake Torque (T_B),

1400 × 10³ = (F_t1 + F_t2) r
1400 × 10³ = (0.776 S + 1.454 S) 175
1400 × 10³ = 390.25 S
S = 1400 × 103 ÷ 390.25
S = 3587 N

The spring force required for braking with Double block brake is 3587 N.

2. Width of Brake Shoes

Let us say b is the Width of the brake shoes in mm.

We know that the projected bearing area for one shoe,

A_b = b(2 r sin θ)
A_b = b(2 × 175 sin 50°)
A_b = 268 b mm²

The normal force on the right-hand side of the shoe,

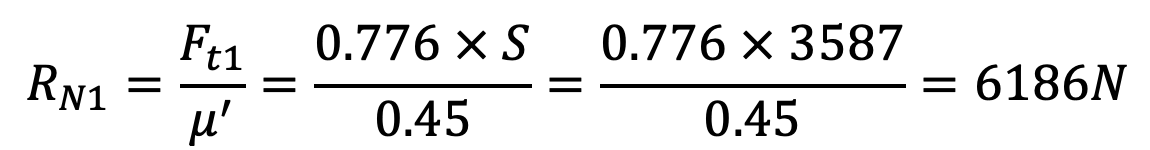
and normal force on the left-hand side of the shoe,

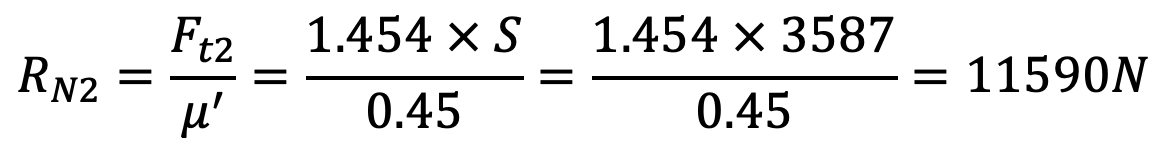
We see that the maximum normal force is on the left-hand side of the shoe. Therefore we shall design the shoe for the maximum normal force i.e. R_N2.

We know that the bearing pressure on the lining material ( p_b),

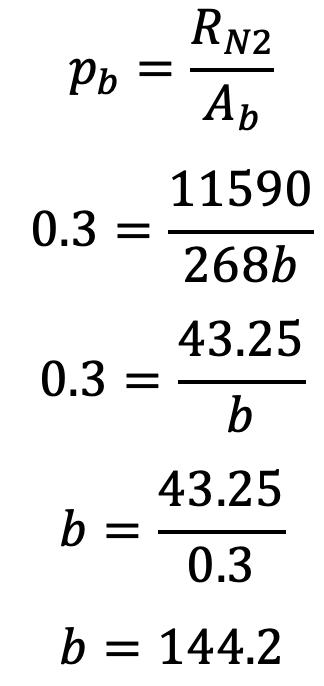
The Width of Brake Shoes is 144.2mm.